[Table des matières]
Sur les sous-algèbres commutatives
de
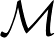 n (K )1
n (K )1
par Jean Fresnel et Michel Matignon
Univ. Bordeaux, CNRS, Bordeaux INP, IMB, UMR 5251, F-33400, Talence, France
Jean.Fresnel@math.u-bordeaux.fr , Michel.Matignon@math.u-bordeaux.fr
Résumé. Soient K un corps commutatif, 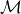 n(K) la K-algèbre des matrices à n lignes et n colonnes à
coefficients dans K. On montre ici que si V est un sous-espace vectoriel de
n(K) la K-algèbre des matrices à n lignes et n colonnes à
coefficients dans K. On montre ici que si V est un sous-espace vectoriel de 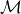 n(K) constitué de matrices qui
commutent deux à deux, alors la dimension de V est majorée par 1 + α(n), où α(n) est égal à r2
si n = 2r ou r(r + 1) si n = 2r + 1. De plus on peut décrire les sous-espaces vectoriels de
dimension 1 + α(n) constitués de matrices qui commutent deux à deux. Cela nous conduit à majorer la
dimension des sous-algèbres commutatives de
n(K) constitué de matrices qui
commutent deux à deux, alors la dimension de V est majorée par 1 + α(n), où α(n) est égal à r2
si n = 2r ou r(r + 1) si n = 2r + 1. De plus on peut décrire les sous-espaces vectoriels de
dimension 1 + α(n) constitués de matrices qui commutent deux à deux. Cela nous conduit à majorer la
dimension des sous-algèbres commutatives de 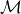 n(K) et à décrire des sous-algèbres commutatives
qui sont de dimension 1 + α(n). Il s’ensuit une caractérisation des sous-groupes commutatifs
maximaux de GLn (K), ainsi que des sous-groupes unipotents maximaux de GLn(K). L’intérêt
de cet article est que les démonstrations utilisent seulement les résultats classiques de l’algèbre
linéaire.
n(K) et à décrire des sous-algèbres commutatives
qui sont de dimension 1 + α(n). Il s’ensuit une caractérisation des sous-groupes commutatifs
maximaux de GLn (K), ainsi que des sous-groupes unipotents maximaux de GLn(K). L’intérêt
de cet article est que les démonstrations utilisent seulement les résultats classiques de l’algèbre
linéaire.
Abstract. Commutative subalgebras of  n(K)
n(K)
Let K be a commutative field,  n(K) the K-algebra of n×n matrices with coefficients in K. We show that
for a subspace V of
n(K) the K-algebra of n×n matrices with coefficients in K. We show that
for a subspace V of  n(K) with elements commuting two by two its dimension is bounded above by 1 + α(n)
where α(n) is equal to r2 for n = 2r and to r(r + 1) for n = 2r + 1. We also describe those for which the
dimension is 1 + α(n). This leads to an upper bound for the dimension of the commutative subalgebras of
n(K) with elements commuting two by two its dimension is bounded above by 1 + α(n)
where α(n) is equal to r2 for n = 2r and to r(r + 1) for n = 2r + 1. We also describe those for which the
dimension is 1 + α(n). This leads to an upper bound for the dimension of the commutative subalgebras of
 n (K) and to the description of these for which the dimension is 1 + α(n). Then we deduce a
characterization of the maximal commutative subgroups of the linear group GLn(K) and also of its maximal
unipotent subgroups. The main interest in this paper is that the proofs use only classical linear
algebra.
n (K) and to the description of these for which the dimension is 1 + α(n). Then we deduce a
characterization of the maximal commutative subgroups of the linear group GLn(K) and also of its maximal
unipotent subgroups. The main interest in this paper is that the proofs use only classical linear
algebra.
Mots-clés : matrice, partie commutative, matrice nilpotente, matrice unipotente, algèbre commutative de matrices, groupe commutatif de matrices.
Dans tout l’article, K désignera un corps commutatif et  n(K) l’algèbre des matrices carrées à n
lignes et n colonnes à coefficients dans K.
n(K) l’algèbre des matrices carrées à n
lignes et n colonnes à coefficients dans K.
Depuis 1905, et peut-être avant, on a étudié les familles de matrices à coefficients dans K constituées d’éléments qui commutent deux à deux.
Si K est le corps des nombres complexes C, Schur a montré en 1905 que le rang de la famille est
majoré par 1 + α(n), où α(n) est égal à r2 si n = 2r ou à r(r + 1) si n = 2r + 1.
On peut aussi dire que α(n) = ⌊(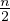 )2⌋ où ⌊x⌋ désigne la partie entière inférieure de
x.
)2⌋ où ⌊x⌋ désigne la partie entière inférieure de
x.
Si V est un sous-espace vectoriel de  n(K) , on dira que V est un sous-espace vectoriel
commutatif si les éléments de V commutent deux à deux. Ainsi, Schur a décrit les sous-espaces
vectoriels commutatifs de dimension 1 + α(n) lorsque K = C (voir ).
n(K) , on dira que V est un sous-espace vectoriel
commutatif si les éléments de V commutent deux à deux. Ainsi, Schur a décrit les sous-espaces
vectoriels commutatifs de dimension 1 + α(n) lorsque K = C (voir ).
Il faut attendre 1944 pour que Jacobson s’intéresse à ce problème lorsque K est quelconque. Il montre la même chose que Schur ; toutefois, il est en difficulté dans le cas où la caractéristique est 2 ().
Cette difficulté sera levée par Gustafson en 1976 avec des méthodes beaucoup plus élaborées (). On trouvera d’autres preuves ou généralisations dans les articles suivants ([Co1], [Co2], [Cow], [K]).
Les auteurs ont découvert un article de jeunesse de Mirzakhani, paru en 1998, suggérant une démonstration élémentaire du théorème de Schur pour un corps quelconque. Toutefois, dans cette note d’une page, elle ne décrit pas les sous-espaces commutatifs qui sont de dimension 1 + α(n) ().
Ici, nous reprenons l’esprit de sa démonstration qui utilise des techniques de l’algèbre linéaire classique. Ce même esprit nous permet de décrire à conjugaison près les sous-espaces vectoriels qui sont de dimension maximale, sans restriction sur la caractéristique de K.
Un sous-espace vectoriel commutatif de  n(K) est contenu dans l’espace vectoriel engendré par
tous les produits finis d’éléments de la famille, qui est donc une sous-algèbre commutative de
n(K) est contenu dans l’espace vectoriel engendré par
tous les produits finis d’éléments de la famille, qui est donc une sous-algèbre commutative de
 n (K). Ainsi, les sous-espaces vectoriels commutatifs de
n (K). Ainsi, les sous-espaces vectoriels commutatifs de  n(K) qui sont maximaux pour
l’inclusion ne sont autres que les sous-algèbres commutatives de
n(K) qui sont maximaux pour
l’inclusion ne sont autres que les sous-algèbres commutatives de  n(K) qui sont maximales pour
l’inclusion.
n(K) qui sont maximales pour
l’inclusion.
Voici un exemple simple. Si A 
 n(K) est telle que χA(X) = mA(X), c’est-à-dire si
le polynôme caractéristique de A est égal à son polynôme minimal, alors on sait que
KIn + KA + ... + KAn-1 est une sous-algèbre commutative, maximale pour l’inclusion et sa
dimension est n. Cela résulte simplement du fait que les matrices qui commutent avec A sont les
polynômes en A (, ex. 4.7.8, p. 192).
n(K) est telle que χA(X) = mA(X), c’est-à-dire si
le polynôme caractéristique de A est égal à son polynôme minimal, alors on sait que
KIn + KA + ... + KAn-1 est une sous-algèbre commutative, maximale pour l’inclusion et sa
dimension est n. Cela résulte simplement du fait que les matrices qui commutent avec A sont les
polynômes en A (, ex. 4.7.8, p. 192).
On a pensé que ce type de sous-algèbre commutative de  n(K) donnait la dimension minimale
parmi les sous-algèbres commutatives de
n(K) donnait la dimension minimale
parmi les sous-algèbres commutatives de  n(K) qui sont maximales pour l’inclusion. En fait,
Courter () a donné en 1965 un exemple de sous-algèbre commutative, maximale pour l’inclusion
dans
n(K) qui sont maximales pour l’inclusion. En fait,
Courter () a donné en 1965 un exemple de sous-algèbre commutative, maximale pour l’inclusion
dans  14 (K), qui est de dimension 13.
14 (K), qui est de dimension 13.
Ceci laisse à penser que la description des sous-algèbres de  n(K), commutatives, maximales
pour l’inclusion, est loin d’être connue. Pour le lecteur curieux, nous reproduisons l’exemple de
Courter à la fin de l’article.
n(K), commutatives, maximales
pour l’inclusion, est loin d’être connue. Pour le lecteur curieux, nous reproduisons l’exemple de
Courter à la fin de l’article.
La connaissance des sous-algèbres commutatives maximales de  n(K) permet de caractériser les
sous-groupes commutatifs de GLn(K) qui sont maximaux dans l’ensemble des sous-groupes
commutatifs de GLn(K).
n(K) permet de caractériser les
sous-groupes commutatifs de GLn(K) qui sont maximaux dans l’ensemble des sous-groupes
commutatifs de GLn(K).
Si T n,0 (K) est le sous-espace vectoriel des matrices triangulaires supérieures dont la diagonale est nulle, alors la connaissance des sous-espaces vectoriels commutatifs, maximaux dans Tn,0(K) permet de caractériser les sous-groupes qui sont maximaux dans l’ensemble des sous-groupes commutatifs unipotents de GLn(K).
2.Sur les sous-espaces vectoriels commutatifs de Tn,0(K)
Dans tout ce qui suit, Tn,0(K) désigne le sous-espace vectoriel de  n(K) constitué des matrices
triangulaires supérieures dont la diagonale est nulle.
n(K) constitué des matrices
triangulaires supérieures dont la diagonale est nulle.
Définition 1. — Soit  une partie de
une partie de  n(K). On dit que
n(K). On dit que  est une partie commutative si, pour
tout A, B
est une partie commutative si, pour
tout A, B 
 , on a AB = BA. Dans ce qui suit, bien souvent
, on a AB = BA. Dans ce qui suit, bien souvent  sera un sous-espace vectoriel de
sera un sous-espace vectoriel de
 n (K); on dira brièvement que
n (K); on dira brièvement que  est un sous-espace vectoriel commutatif, si c’est aussi une
partie commutative ; on prendra garde que cela ne suppose pas que S est stable par
produit.
est un sous-espace vectoriel commutatif, si c’est aussi une
partie commutative ; on prendra garde que cela ne suppose pas que S est stable par
produit.
Proposition 1. — (1) Soit V un sous-espace vectoriel commutatif de Tn,0(K) avec n ≥ 2, qui est
maximal pour l’inclusion. Alors pour tout A,B  V on a AB
V on a AB  V .
V .
(2) Soit V un sous-espace vectoriel commutatif de  n(K), constitué de nilpotents, qui est maximal
pour cette propriété. Alors pour tout A,B
n(K), constitué de nilpotents, qui est maximal
pour cette propriété. Alors pour tout A,B  V , on a AB
V , on a AB  V .
V .
Démonstration Montrons le point (1). Soit V ʹ le sous-espace vectoriel de  n(K) engendré par V
et par les AB où A,B
n(K) engendré par V
et par les AB où A,B  V . Clairement V ʹ est un sous-espace vectoriel commutatif de Tn,0(K),
ainsi la maximalité de V implique que V = V ʹ ; ce qui montre (1). Le même argument
permet de démontrer (2) puisqu’un produit commutatif de deux nilpotents est encore
nilpotent.
cqfd
V . Clairement V ʹ est un sous-espace vectoriel commutatif de Tn,0(K),
ainsi la maximalité de V implique que V = V ʹ ; ce qui montre (1). Le même argument
permet de démontrer (2) puisqu’un produit commutatif de deux nilpotents est encore
nilpotent.
cqfd
Dans ce qui suit Ei,j désigne la matrice telle que Ei,j(k,l) = δi,kδj,l. Enfin  s,t(K) désigne le
K-espace vectoriel des matrices à s lignes et t colonnes.
s,t(K) désigne le
K-espace vectoriel des matrices à s lignes et t colonnes.
Théorème 1. — Soit V un sous-espace vectoriel commutatif de Tn,0(K) avec n ≥ 2. Alors on a dimKV ≤ α(n).
⊳ Soient n = 2r ≥ 2 et  :=
:= 
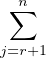 KEi,j, l’ensemble des matrices
KEi,j, l’ensemble des matrices ![[ ]
0 A
0 0](/numeros/RMS130-4/RMS130-44x.png) appartenant à
Tn,0(K) où A
appartenant à
Tn,0(K) où A 
 r(K). Ainsi, l’ensemble
r(K). Ainsi, l’ensemble  est un sous-espace vectoriel commutatif de
Tn,0(K) avec dim
est un sous-espace vectoriel commutatif de
Tn,0(K) avec dim = α(n) ; de plus, on a AB = 0 si A,B
= α(n) ; de plus, on a AB = 0 si A,B 
 .
.
⊳ Soient n = 2r + 1 ≥ 3,  1 :=
1 := 
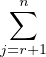 KEi,j, i.e.
KEi,j, i.e.  1 est l’ensemble des matrices
1 est l’ensemble des matrices
![[0A]
00](/numeros/RMS130-4/RMS130-47x.png)
 Tn,0(K) où A
Tn,0(K) où A 
 r,r+1(K). Ainsi
r,r+1(K). Ainsi  1 est un sous-espace vectoriel commutatif de
Tn,0(K) avec dim
1 est un sous-espace vectoriel commutatif de
Tn,0(K) avec dim 1 = α(n).
1 = α(n).
Soit  2 :=
2 := 
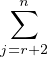 KEi,j, formé des matrices
KEi,j, formé des matrices ![[ 0 A ]
0 0](/numeros/RMS130-4/RMS130-410x.png)
 Tn,0(K) où A
Tn,0(K) où A 
 r+1,r(K). Ainsi
r+1,r(K). Ainsi
 2 est un sous-espace vectoriel commutatif de Tn,0(K) avec dim
2 est un sous-espace vectoriel commutatif de Tn,0(K) avec dim 2 = α(n).
2 = α(n).
Alors  1 et
1 et  2 sont deux sous-espaces vectoriels commutatifs de Tn,0(K) vérifiant
dim
2 sont deux sous-espaces vectoriels commutatifs de Tn,0(K) vérifiant
dim i = α(n) pour i = 1,2 ; de plus, on a AB = 0 si A,B
i = α(n) pour i = 1,2 ; de plus, on a AB = 0 si A,B 
 i pour i = 1,2.
i pour i = 1,2.
Démonstration C’est essentiellement celle de . Le théorème est immédiat pour T2,0(K), on le suppose vrai pour Tn-1,0(K) avec n ≥ 3 ; il s’agit de montrer que le théorème est satisfait pour Tn,0(K).
∙ Soient
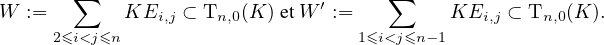
 W (resp. tel que
fʹ(AB) = fʹ(A)fʹ(B) pour tout A,B
W (resp. tel que
fʹ(AB) = fʹ(A)fʹ(B) pour tout A,B  Wʹ).
Wʹ).
Soit t : T n,0 (K) → W , tʹ : Tn,0(K) → Wʹ définis comme il suit. Si A = [ai,j]  Tn,0(K),
alors
Tn,0(K),
alors
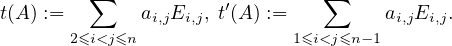
Alors V 1 := V ∩ 
 KE1,j
KE1,j (resp. V 2 := V ∩
(resp. V 2 := V ∩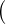
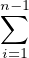 KEi,n
KEi,n ) est le noyau de la restriction à V
de t (resp. tʹ). Il suit de cela que
) est le noyau de la restriction à V
de t (resp. tʹ). Il suit de cela que
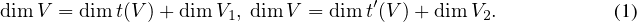
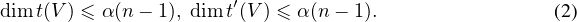
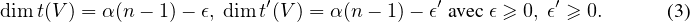
∙ Soient θ1  V 1 , θ2
V 1 , θ2  V 2, montrons que θ1θ2 = 0. On a
V 2, montrons que θ1θ2 = 0. On a
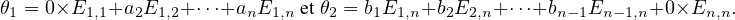
Compte tenu des relations Ei,jEk,l = 0 si j≠k et Ei,jEj,l = Ei,l, on a facilement θ2θ1 = 0.
Comme θ1 , θ2  V , on a θ1θ2 = θ2θ1 = 0.
V , on a θ1θ2 = θ2θ1 = 0.
∙ Or θ1 θ2 = (0 × b1 + a2b2 +  + an-1bn-1 + an × 0)E1,n, ainsi
+ an-1bn-1 + an × 0)E1,n, ainsi
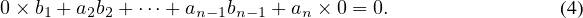
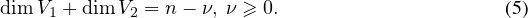
Compte tenu des relations (1), (3), (5), on a
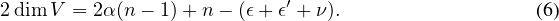
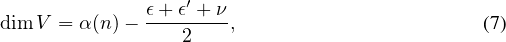
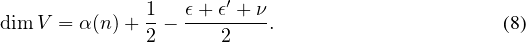
Corollaire 1. — Soit V un sous-espace vectoriel commutatif de  n(K) avec n ≥ 2, constitué de
nilpotents. Alors dimV ≤ α(n).
n(K) avec n ≥ 2, constitué de
nilpotents. Alors dimV ≤ α(n).
Démonstration Il suit de la proposition 4 de l’appendice qu’il existe P  GLn(K) tel que
PV P-1 ⊂ T n,0 (K). Alors le corollaire est conséquence immédiate du théorème 1.
cqfd
GLn(K) tel que
PV P-1 ⊂ T n,0 (K). Alors le corollaire est conséquence immédiate du théorème 1.
cqfd
Théorème 2. — Soient n ≥ 2, α(n),  ,
,  1,
1,  2, définis dans l’énoncé du théorème
1.
2, définis dans l’énoncé du théorème
1.
Soit V un sous-espace vectoriel commutatif de Tn,0(K) avec dimV = α(n).
(1) Si n = 2r ≥ 2, alors V =  .
.
(2) Si n = 2r + 1 ≥ 5, alors V =  1 ou V =
1 ou V =  2.
2.
(3) Si n = 3 alors les sous-espaces vectoriels commutatifs, de dimension α(3) = 2 de T3,0(K) sont
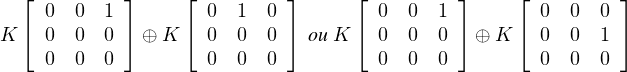
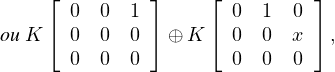
Démonstration (1) ⊳ Si n = 2r et dimV = α(n), il suit de (7) que ε = εʹ = 0 ; il en résulte que dimt(V ) = dim tʹ(V ) = α(n - 1).
⊳ Si n = 2r + 1 et dimV = α(n), il suit de (8) que ε = 0 ou εʹ = 0 ; par conséquent, dimt(V ) = α(n - 1) si ε = 0 et dimtʹ(V ) = α(n - 1) si εʹ = 0.
Nous montrons à présent le théorème par récurrence sur n, en l’initialisant à n = 2, 3 et 4.
(2) Montrons le théorème pour n = 2,3. Pour n = 2, il est clair que V = T2,0(K).
On suppose maintenant que n = 3. Comme dimV = 2, il existe A = 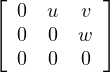
 V avec
(u, w)≠ (0, 0). On a A2≠0 si et seulement si uw≠0.
V avec
(u, w)≠ (0, 0). On a A2≠0 si et seulement si uw≠0.
⊳ Supposons d’abord uw≠0. Dans ce cas, on a χA(X) = mA(X) = X3. Par conséquent,
KA + KA2 = KA⊕KA2 est un sous-espace vectoriel commutatif de T3,0(K) de dimension 2.
D’autre part si (A,B) est une base de V , sachant que V est commutatif, il suit de (, ex. 4.7.8, p.
192) que B  KA ⊕ KA2, ainsi V = KA ⊕ KA2. Facilement
KA ⊕ KA2, ainsi V = KA ⊕ KA2. Facilement
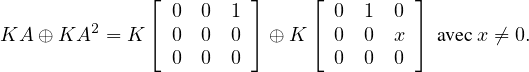
⊳ Supposons que u≠0 et w = 0, on montre facilement que le commutant de A dans T3,0(K) est
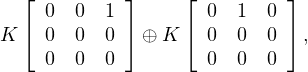
⊳ De même, si u = 0 et si w≠0, on a V = K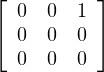 ⊕ K
⊕ K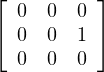 .
.
(3) Montrons le théorème pour n = 4.
On a donc dim V = 4, il suit de 1. que dimt(V ) = 2, dimV 1 = 2 et aussi dimtʹ(V ) = 2, dimV 2 = 2. Il suit de 2. que les sous-espaces vectoriels commutatifs, de dimension 2 de T3,0(K) sont
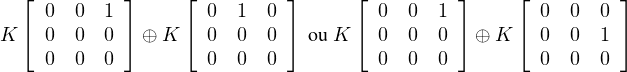
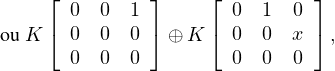
(a) Il s’agit de montrer que t(V ) ne peut être le troisième cas. Supposons le contraire, i.e.
t(V ) = K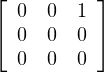 ⊕ K
⊕ K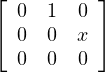 avec x≠0.
avec x≠0.
Il existe donc A, B  V avec
V avec
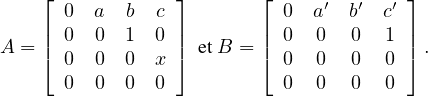
Montrons d’abord que V 1 = KD ⊕ KE, avec
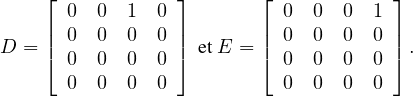
Soit C = 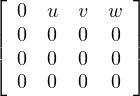
 V 1. De la relation CB = BC = 0, on déduit facilement que u = 0,
ainsi V 1 ⊂ KD ⊕ KE et pour des raisons de dimension, on a bien V 1 = KD ⊕ KE.
V 1. De la relation CB = BC = 0, on déduit facilement que u = 0,
ainsi V 1 ⊂ KD ⊕ KE et pour des raisons de dimension, on a bien V 1 = KD ⊕ KE.
Enfin de la relation DA = AD = 0, on déduit que x = 0, ce qui contredit x≠0.
Par une méthode analogue on peut montrer que
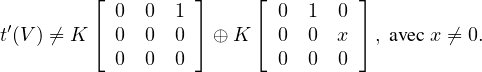
(b) Supposons que t(V ) = K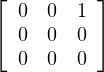 ⊕ K
⊕ K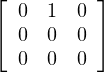 , il s’agit de montrer que
V = KE1,3 ⊕ KE1,4 ⊕ KE2,3 ⊕ KE2,4. Montrons d’abord que V 1 = KE1,3 ⊕ KE1,4.
, il s’agit de montrer que
V = KE1,3 ⊕ KE1,4 ⊕ KE2,3 ⊕ KE2,4. Montrons d’abord que V 1 = KE1,3 ⊕ KE1,4.
Soit U = uE1,2 + vE1,3 + wE1,4  V 1 et R = uʹE1,2 + vʹE1,3 + wʹE1,4 + E2,3
V 1 et R = uʹE1,2 + vʹE1,3 + wʹE1,4 + E2,3  V tel que
t(R) = E2,3 . Il suit de la relation UR = RU = 0 que u = 0 ; ainsi donc
V tel que
t(R) = E2,3 . Il suit de la relation UR = RU = 0 que u = 0 ; ainsi donc
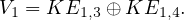
 V tels que t(Z) = E2,3, t(T) = E2,4, lorsque l’on pose
Z = uʹ E1,2 + E2,3, T = uʹʹE1,2 + E2,4. Alors il suit de ZT = TZ que uʹ = 0 et
uʹʹ = 0.
V tels que t(Z) = E2,3, t(T) = E2,4, lorsque l’on pose
Z = uʹ E1,2 + E2,3, T = uʹʹE1,2 + E2,4. Alors il suit de ZT = TZ que uʹ = 0 et
uʹʹ = 0.
Cela montre bien que V = KE1,3 ⊕ KE1,4 ⊕ KE2,3 ⊕ KE2,4.
(c) Il reste à montrer que t(V ) = KE1,4 ⊕ KE2,4 est impossible.
Soit A = uE1,2 + vE1,3 + wE1,4  V 1, B = uʹE1,2 + vʹE1,3 + wʹE1,4 + E2,4
V 1, B = uʹE1,2 + vʹE1,3 + wʹE1,4 + E2,4  V ,
C = uʹʹ E1,2 + vʹʹE1,3 + wʹʹE1,4 + E3,4
V ,
C = uʹʹ E1,2 + vʹʹE1,3 + wʹʹE1,4 + E3,4  V , tels que t(B) = E2,4, t(C) = E3,4.
V , tels que t(B) = E2,4, t(C) = E3,4.
Il suit de AB = BA = 0 que u = 0, de AC = CA = 0 que v = 0. Ainsi V 1 ⊂ KE1,4, ce qui est impossible puisque dimV 1 = 2.
(4) On suppose que n ≥ 5 et que le théorème est satisfait pour n - 1.
(a) On suppose que n = 2r + 1 ≥ 5. Il suit du premier alinéa que dimt(V ) = α(n - 1) ou que dimtʹ(V ) = α(n - 1).
On suppose que dimt(V ) = α(n - 1), alors on a
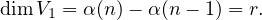
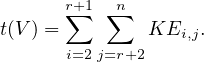
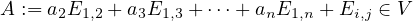
 + bnE1,n
+ bnE1,n  V 1. Facilement, on obtient
BA = bi E1,j , AB = 0. Ainsi bi = 0 pour 2 ≤ i ≤ r + 1. Il en suit que V 1 =
V 1. Facilement, on obtient
BA = bi E1,j , AB = 0. Ainsi bi = 0 pour 2 ≤ i ≤ r + 1. Il en suit que V 1 = 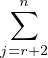 KE1,j.
KE1,j.
Soit r + 2 ≤ j < jʹ≤ n (on a r ≥ 2). Il suit de ce qui précède qu’il existe S,T  V avec
t(S) = Ei,j , t(T) = Ei,jʹ avec S = s2E1,2 + s3E1,3 +
V avec
t(S) = Ei,j , t(T) = Ei,jʹ avec S = s2E1,2 + s3E1,3 +  + sr+1E1,r+1 + Ei,j et
T = t2 E1,2 + t3 E1,3 +
+ sr+1E1,r+1 + Ei,j et
T = t2 E1,2 + t3 E1,3 +  + tr+1E1,r+1 + Ei,jʹ.
+ tr+1E1,r+1 + Ei,jʹ.
Facilement, on a ST = siE1,jʹ, TS = tiE1,j. Comme ST = TS, il suit que si = 0, ti = 0 pour
2 ≤ i ≤ r + 1. Ainsi Ei,j  V pour 1 ≤ i ≤ r + 1, r + 2 ≤ j ≤ n. En conclusion, on a
V ⊃
V pour 1 ≤ i ≤ r + 1, r + 2 ≤ j ≤ n. En conclusion, on a
V ⊃ 
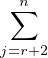 KEi,j et pour des raisons de dimension, on a bien V =
KEi,j et pour des raisons de dimension, on a bien V =  2.
2.
Sous l’hypothèse dimtʹ(V ) = α(n - 1), on aurait par une démonstration analogue
V =  1 .
1 .
(b) On suppose que n = 2r ≥ 5. On a donc dimV = α(n) = r2, il suit du premier alinéa que
dimt(V ) = α(n - 1) = r2 - r et donc dimV 1 = r. Il suit alors de l’hypothèse de récurrence
que t(V ) = 
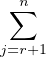 KEi,j ou t(V ) =
KEi,j ou t(V ) = 
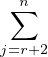 KEi,j. Il s’agit d’exclure ce dernier
cas.
KEi,j. Il s’agit d’exclure ce dernier
cas.
Supposons que t(V ) = 
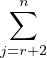 KEi,j. Soit A := a2E1,2 + a3E1,3 +
KEi,j. Soit A := a2E1,2 + a3E1,3 +  + anE1,n
+ anE1,n  V 1. Soit
B = b2 E1,2 + b3 E1,3 +
V 1. Soit
B = b2 E1,2 + b3 E1,3 +  + bnE1,n + Ei,j
+ bnE1,n + Ei,j  V et t(B) = Ei,j où 2 ≤ i ≤ r + 1 et
r + 2 ≤ j ≤ n. Facilement AB = aiE1,j, BA = 0 et comme AB = BA on a donc ai = 0 pour
2 ≤ i ≤ r + 1. Ce qui veut dire que V 1 ⊂
V et t(B) = Ei,j où 2 ≤ i ≤ r + 1 et
r + 2 ≤ j ≤ n. Facilement AB = aiE1,j, BA = 0 et comme AB = BA on a donc ai = 0 pour
2 ≤ i ≤ r + 1. Ce qui veut dire que V 1 ⊂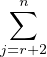 KE1,j et c’est impossible pour des raisons de
dimension. Ainsi
KE1,j et c’est impossible pour des raisons de
dimension. Ainsi
Par une méthode analogue à (4)(a), on peut montrer que V 1 ⊂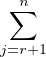 KE1,j, et donc que
V 1 =
KE1,j, et donc que
V 1 = 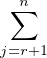 KE1,j.
KE1,j.
Soient 2 ≤ i ≤ r, r + 1 ≤ j ≤ n, il reste à montrer que Ei,j  V . Soient r + 1 ≤ j < jʹ≤ n
(2r ≥ 5). Il suit de ce qui précède qu’il existe S,T
V . Soient r + 1 ≤ j < jʹ≤ n
(2r ≥ 5). Il suit de ce qui précède qu’il existe S,T  V avec t(S) = Ei,j, t(T) = Ei,jʹ et
S = s2 E1,2 + s3 E1,3 +
V avec t(S) = Ei,j, t(T) = Ei,jʹ et
S = s2 E1,2 + s3 E1,3 +  + srE1,r + Ei,j, T = t2E1,2 + t3E1,3 +
+ srE1,r + Ei,j, T = t2E1,2 + t3E1,3 +  + trE1,r + Ei,jʹ.
+ trE1,r + Ei,jʹ.
Facilement ST = siE1,jʹ, TS = tiE1,j ; comme ST = TS, on a si = 0, ti = 0 pour 2 ≤ i ≤ r.
Ainsi Ei,j  V pour 2 ≤ i ≤ r + 1 et r + 2 ≤ j ≤ n. Ce qui montre que l’égalité V =
V pour 2 ≤ i ≤ r + 1 et r + 2 ≤ j ≤ n. Ce qui montre que l’égalité V =  .
cqfd
.
cqfd
Corollaire 2. — Soit V un sous-espace vectoriel commutatif de  n(K) avec n ≥ 2,
constitué de nilpotents avec dimV = α(n). Alors il existe P
n(K) avec n ≥ 2,
constitué de nilpotents avec dimV = α(n). Alors il existe P  GLn(K) avec les propriétés
suivantes.
GLn(K) avec les propriétés
suivantes.
(1) Si n = 2r ≥ 2, alors PV P-1 =  .
.
(2) Si n = 2r + 1 ≥ 5, alors PV P-1 =  1 ou PV P-1 =
1 ou PV P-1 =  2.
2.
(3) Si n = 3, alors
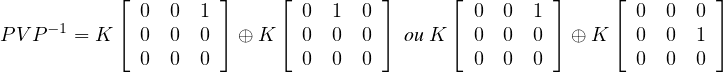
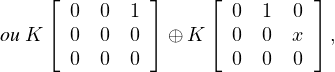
Démonstration Il suit de la proposition 4 de l’appendice qu’il existe P  GLn(K) tel que
PV P-1 ⊂ T n,0 (K). Alors le corollaire est conséquence immédiate du théorème 2.
cqfd
GLn(K) tel que
PV P-1 ⊂ T n,0 (K). Alors le corollaire est conséquence immédiate du théorème 2.
cqfd
3.Sur
les
sous-algèbres
commutatives
de
 n (K)
n (K)
Proposition 2. — Soit  une partie de
une partie de  n(K) avec n ≥ 1. Les propriétés suivantes sont
équivalentes.
n(K) avec n ≥ 1. Les propriétés suivantes sont
équivalentes.
(i) La partie  est un sous-espace vectoriel commutatif de
est un sous-espace vectoriel commutatif de  n(K) qui est maximal pour
l’inclusion ;
n(K) qui est maximal pour
l’inclusion ;
(ii) la partie  est une sous-algèbre commutative de
est une sous-algèbre commutative de  n(K) qui est maximale pour
l’inclusion.
n(K) qui est maximale pour
l’inclusion.
Démonstration Montrons (i) implique (ii). Soit  ʹ le sous-espace vectoriel de
ʹ le sous-espace vectoriel de  n(K) engendré par
n(K) engendré par
 , In et par les AB où A,B
, In et par les AB où A,B 
 . Clairement
. Clairement  ʹ est un sous-espace vectoriel commutatif, ainsi la
maximalité de
ʹ est un sous-espace vectoriel commutatif, ainsi la
maximalité de  implique que
implique que  =
=  ʹ. Cela montre que
ʹ. Cela montre que  est une sous-algèbre unitaire de
est une sous-algèbre unitaire de  n(K)
. Il reste à montrer que
n(K)
. Il reste à montrer que  est maximale comme sous-algèbre commutative. En effet s’il existe une
sous-algèbre commutative
est maximale comme sous-algèbre commutative. En effet s’il existe une
sous-algèbre commutative  ʹʹ avec
ʹʹ avec  ⊂
⊂ ʹʹ, comme
ʹʹ, comme  ʹʹ est en particulier un sous-espace vectoriel
commutatif, la maximalité de
ʹʹ est en particulier un sous-espace vectoriel
commutatif, la maximalité de  implique
implique  =
=  ʹʹ, ainsi
ʹʹ, ainsi  est une sous-algèbre commutative,
maximale.
est une sous-algèbre commutative,
maximale.
Montrons (ii) implique (i). Soit  ʹ un sous-espace vectoriel, commutatif de
ʹ un sous-espace vectoriel, commutatif de  n(K) avec
n(K) avec
 ⊂
⊂  ʹ et
ʹ et  ʹʹ la sous-algèbre unitaire de
ʹʹ la sous-algèbre unitaire de  n(K) engendrée par
n(K) engendrée par  ʹ, clairement
ʹ, clairement  ʹʹ est une
sous-algèbre commutative. La maximalité de
ʹʹ est une
sous-algèbre commutative. La maximalité de  implique
implique  =
=  ʹʹ et donc
ʹʹ et donc  =
=  ʹ ; ce
qui veut dire que
ʹ ; ce
qui veut dire que  est un sous-espace vectoriel commutatif maximal pour l’inclusion.
cqfd
est un sous-espace vectoriel commutatif maximal pour l’inclusion.
cqfd
Lemme 1. — Soient n1,n2,…,ns des entiers tels que 1 ≤ n1 ≤ n2 ≤ ≤ ns et posons
n := n1 + n2 +
≤ ns et posons
n := n1 + n2 +  + ns, s ≥ 1. Alors on a
+ ns, s ≥ 1. Alors on a
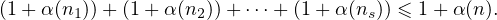
De plus si s ≥ 2, on a
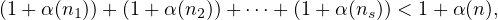
sauf si s = 2, n1 = 1, n2 = 2 auquel cas on a (1 + α(1)) + (1 + α(2)) = 1 + α(3).
Démonstration Elle se fait sans difficulté par récurrence sur s. cqfd
Théorème 3. — Soit  un sous-espace vectoriel commutatif de
un sous-espace vectoriel commutatif de  n(K) avec n ≥ 4. Alors on
a
n(K) avec n ≥ 4. Alors on
a
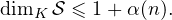
Démonstration Soient Kalg la clôture algébrique de K,  alg le sous-Kalg-espace vectoriel de
Mn (Kalg ) engendré par
alg le sous-Kalg-espace vectoriel de
Mn (Kalg ) engendré par  ; bien entendu
; bien entendu  alg est commutatif et
alg est commutatif et
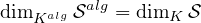
Notons 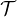 :=
:=  alg ; il suit de la partie matricielle de la proposition 4 de l’appendice qu’il existe
P
alg ; il suit de la partie matricielle de la proposition 4 de l’appendice qu’il existe
P  GLn (Kalg ) tel que P
GLn (Kalg ) tel que P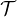 P-1 s’injecte dans le produit
P-1 s’injecte dans le produit 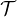 1 ×
1 ×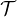 2 × ... ×
2 × ... ×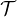 s où
s où 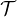 i est un
sous-espace vectoriel de
i est un
sous-espace vectoriel de  ni(Kalg) de la forme KalgIni si ni = 1 et KalgIni +
ni(Kalg) de la forme KalgIni si ni = 1 et KalgIni +  i où
i où
 i ⊂ T ni ,0 (Kalg) si ni ≥ 2 ; de plus on a 1 ≤ n1 ≤ n2 ≤ ... ≤ ns, n = n1 + n2 + ... + ns,
s ≥ 1 et
i ⊂ T ni ,0 (Kalg) si ni ≥ 2 ; de plus on a 1 ≤ n1 ≤ n2 ≤ ... ≤ ns, n = n1 + n2 + ... + ns,
s ≥ 1 et  i est un sous-espace vectoriel commutatif de Tni,0(Kalg). Il suit donc du
théorème 1 que dimKalg
i est un sous-espace vectoriel commutatif de Tni,0(Kalg). Il suit donc du
théorème 1 que dimKalg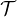 i ≤ 1 + α(ni). Ainsi le théorème est conséquence du lemme 1.
cqfd
i ≤ 1 + α(ni). Ainsi le théorème est conséquence du lemme 1.
cqfd
Théorème 4. — Soit  une sous-algèbre commutative, unitaire de
une sous-algèbre commutative, unitaire de  n(K) avec n ≥ 4 et
dimK
n(K) avec n ≥ 4 et
dimK = 1 + α(n). Alors il existe P
= 1 + α(n). Alors il existe P  GLn(K) avec P
GLn(K) avec P P-1 = KIn ⊕
P-1 = KIn ⊕ si n est pair et
P
si n est pair et
P P-1 = KIn ⊕
P-1 = KIn ⊕ 1 ou P
1 ou P P-1 = KIn ⊕
P-1 = KIn ⊕ 2 si n est impair ;
2 si n est impair ;  ,
,  1,
1,  2 sont définis au
théorème 1.
2 sont définis au
théorème 1.
En particulier  est une algèbre locale dont l’idéal maximal
est une algèbre locale dont l’idéal maximal  est tel que si A,B
est tel que si A,B 
 , alors on a
AB = 0 et de plus
, alors on a
AB = 0 et de plus  = KIn ⊕
= KIn ⊕ .
.
Démonstration
∙ On reprend la démonstration du théorème 3.
Notons 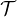 :=
:=  alg, il suit de la partie matricielle de la proposition 4 de l’appendice qu’il existe
P
alg, il suit de la partie matricielle de la proposition 4 de l’appendice qu’il existe
P  GL n (Kalg ) tel que P
GL n (Kalg ) tel que P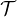 P-1 s’injecte dans le produit
P-1 s’injecte dans le produit 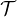 1 ×
1 ×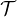 2 × ... ×
2 × ... ×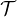 s où
s où 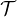 i est un
sous-espace vectoriel de
i est un
sous-espace vectoriel de  ni(Kalg) de la forme KalgIni si ni = 1 et KalgIni +
ni(Kalg) de la forme KalgIni si ni = 1 et KalgIni +  i où
i où
 i ⊂ T ni ,0 (Kalg) si ni ≥ 2 ; de plus on a 1 ≤ n1 ≤ n2 ≤ ... ≤ ns, n = n1 + n2 +
i ⊂ T ni ,0 (Kalg) si ni ≥ 2 ; de plus on a 1 ≤ n1 ≤ n2 ≤ ... ≤ ns, n = n1 + n2 +  + ns,
s ≥ 1 et
+ ns,
s ≥ 1 et  i est un sous-espace vectoriel commutatif de Tni,0(Kalg). Il suit donc du théorème 1
que dim Kalg
i est un sous-espace vectoriel commutatif de Tni,0(Kalg). Il suit donc du théorème 1
que dim Kalg 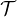 i ≤ 1 + α(ni). On a donc
i ≤ 1 + α(ni). On a donc
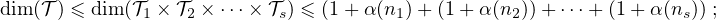
 alg P-1 ⊂ KalgIn ⊕
alg P-1 ⊂ KalgIn ⊕ où
où  ⊂ Tn,0(Kalg) et où
⊂ Tn,0(Kalg) et où  est un sous-espace vectoriel commutatif
de T n,0 (Kalg ) de dimension α(n).
est un sous-espace vectoriel commutatif
de T n,0 (Kalg ) de dimension α(n).
Il suit alors du théorème 2 que, si n est pair, on a
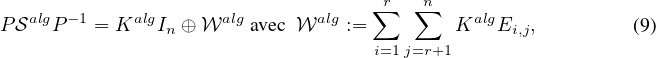
et que, si n est impair, on a
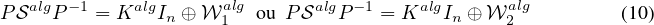

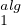 :=
:= 
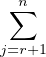 KalgEi,j,
KalgEi,j, 
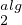 :=
:= 
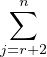 KalgEi,j.
KalgEi,j.
∙ On souhaite montrer qu’il existe Q  GLn(K) tel que Q
GLn(K) tel que Q Q-1 = KIn ⊕
Q-1 = KIn ⊕ si n est pair et
Q
si n est pair et
Q Q-1 = KIn ⊕
Q-1 = KIn ⊕ 1 ou Q
1 ou Q Q-1 = KIn ⊕
Q-1 = KIn ⊕ 2 si n est impair.
2 si n est impair.
Il suit de (9) et (10) que  alg = KalgIn ⊕
alg = KalgIn ⊕ où
où  est un idéal maximal de
est un idéal maximal de  alg tel que si
A, B
alg tel que si
A, B 
 , alors on a AB = 0 ; en particulier
, alors on a AB = 0 ; en particulier  est constitué de nilpotents. Ainsi les inversibles de
est constitué de nilpotents. Ainsi les inversibles de
 alg sont les éléments de la forme λIn + N avec λ
alg sont les éléments de la forme λIn + N avec λ  Kalg -{0} et N
Kalg -{0} et N 
 ; et donc
; et donc  est
l’ensemble des non-inversibles de
est
l’ensemble des non-inversibles de  alg.
alg.
Soit A 
 qui est inversible de
qui est inversible de  , donc inversible de
, donc inversible de  alg, ce qui veut dire que A = λIn + N avec
λ
alg, ce qui veut dire que A = λIn + N avec
λ  Kalg - {0} et N
Kalg - {0} et N 
 et donc N est nilpotent. Il suit de cela que le polynôme caractéristique
de A est de la forme χA(X) = (X - λ)n
et donc N est nilpotent. Il suit de cela que le polynôme caractéristique
de A est de la forme χA(X) = (X - λ)n  K[X], avec λ
K[X], avec λ  Kalg.
Kalg.
∙ Montrons que λ  K et pour cela que
K et pour cela que  contient un élément non-inversible qui n’est pas
nul.
contient un élément non-inversible qui n’est pas
nul.
Soit 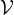 :=
:= 
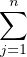 KEi,j, on a donc dim
KEi,j, on a donc dim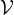 = n(n - 1) et tout élément de
= n(n - 1) et tout élément de 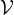 est non-inversible.
Comme dim K
est non-inversible.
Comme dim K  = 1 + α(n), il suit que pour n ≥ 4, on a dim
= 1 + α(n), il suit que pour n ≥ 4, on a dim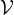 + dim
+ dim > n2, cela veut dire
qu’il existe C
> n2, cela veut dire
qu’il existe C 
 non-inversible de
non-inversible de  n(K) et C≠0 ; il suit pour des raisons de déterminant que C
est un élément non-inversible de
n(K) et C≠0 ; il suit pour des raisons de déterminant que C
est un élément non-inversible de  n(Kalg), ainsi C
n(Kalg), ainsi C 
 . Sachant que A - λIn
. Sachant que A - λIn 
 et
C
et
C 
 , on a (A - λIn)C = 0 ; il suit de cela que λ
, on a (A - λIn)C = 0 ; il suit de cela que λ  K. En effet si λ
K. En effet si λ K, alors la
famille (1, λ) est K-libre, il suit de cela que si U,V
K, alors la
famille (1, λ) est K-libre, il suit de cela que si U,V 
 n(K) et si U + λV = 0, alors
U = V = 0; ainsi la relation AC - λC = 0 implique en particulier que C = 0, ce qui est une
contradiction.
n(K) et si U + λV = 0, alors
U = V = 0; ainsi la relation AC - λC = 0 implique en particulier que C = 0, ce qui est une
contradiction.
∙ Il suit du paragraphe précédent que, si A 
 , il existe λA
, il existe λA  K avec χA(X) = (X -λA)n. Alors
la proposition 4 de l’appendice, version matricielle dit qu’il existe Q
K avec χA(X) = (X -λA)n. Alors
la proposition 4 de l’appendice, version matricielle dit qu’il existe Q  GLn(K) tel que
Q
GLn(K) tel que
Q Q-1 = KIn ⊕
Q-1 = KIn ⊕ où
où  est un sous-espace vectoriel commutatif de Tn,0(K). Sachant que
dim
est un sous-espace vectoriel commutatif de Tn,0(K). Sachant que
dim = 1 + α(n) et que dim
= 1 + α(n) et que dim ≤ α(n), on a donc dim
≤ α(n), on a donc dim = α(n) et alors
= α(n) et alors  est décrit par le
théorème 2. Ce qui achève la démonstration. cqfd
est décrit par le
théorème 2. Ce qui achève la démonstration. cqfd
Remarque. — Les cas n = 2, n = 3.
(1) Soit  une sous-algèbre commutative de
une sous-algèbre commutative de  2(K) avec dim
2(K) avec dim = 1 + α(2) = 2. Alors il existe
P
= 1 + α(2) = 2. Alors il existe
P  GL 2 (K) avec P
GL 2 (K) avec P P-1 = KI2 ⊕ KB et B =
P-1 = KI2 ⊕ KB et B = ![[ ]
0 b
1 a](/numeros/RMS130-4/RMS130-494x.png) .
.
Pour montrer cela, il suffit de remarquer que  , qui est de dimension 2, contient une matrice dont le
polynôme minimal est de degré 2.
, qui est de dimension 2, contient une matrice dont le
polynôme minimal est de degré 2.
(2) Soit  une sous-algèbre commutative de
une sous-algèbre commutative de  3(K) avec dim
3(K) avec dim = 1 + α(3) = 3.
= 1 + α(3) = 3.
⊳ Alors il existe P  GL3(K) avec
GL3(K) avec
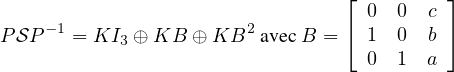
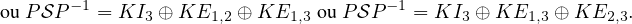
Si K = F 2 , il faut ajouter P P-1 = KE1,1 ⊕ KE2,2 ⊕ KE3,3.
P-1 = KE1,1 ⊕ KE2,2 ⊕ KE3,3.
Le premier cas correspond au fait que  qui est de dimension 3 contient une matrice dont le
polynôme minimal est de degré 3.
qui est de dimension 3 contient une matrice dont le
polynôme minimal est de degré 3.
Les autres cas correspondent au fait que toutes les matrices de  ont un polynôme minimal qui est
de degré au plus 2.
ont un polynôme minimal qui est
de degré au plus 2.
⊳ On rappelle que f :  n(K) →
n(K) → n(K) est un automorphisme intérieur lorsqu’il existe
A
n(K) est un automorphisme intérieur lorsqu’il existe
A  GLn (K) telle que, pour tout X
GLn (K) telle que, pour tout X 
 n(K), f(X) = AXA-1. Alors, il n’existe pas
d’automorphisme intérieur f de
n(K), f(X) = AXA-1. Alors, il n’existe pas
d’automorphisme intérieur f de  3(K) avec
3(K) avec
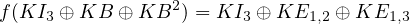
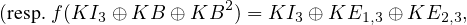
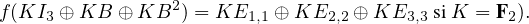
Il suffit pour cela de considérer le degré des polynômes minimaux.
Par ailleurs, il n’existe pas d’automorphisme intérieur f de  3(K) avec
3(K) avec
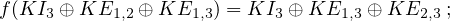
De même si K = F2, il n’existe pas d’automorphisme intérieur f de  3(K) avec
3(K) avec
 3(K) avec f(KI3 ⊕ KE1,3 ⊕ KE2,3) = KE1,1 ⊕ KE2,2 ⊕ KE3,3.
3(K) avec f(KI3 ⊕ KE1,3 ⊕ KE2,3) = KE1,1 ⊕ KE2,2 ⊕ KE3,3.
4. Sur les sous-groupes commutatifs de GLn(K)
Si  est un sous-groupe commutatif de GLn(K), la sous-K-algèbre K[
est un sous-groupe commutatif de GLn(K), la sous-K-algèbre K[ ] de
] de  n(K) engendrée
par
n(K) engendrée
par  est commutative et on a
est commutative et on a  ⊂ K[
⊂ K[ ]×, où K[
]×, où K[ ]× désigne le groupe des inversibles de K[
]× désigne le groupe des inversibles de K[ ]. En
particulier si
]. En
particulier si  est un sous-groupe commutatif de GLn(K), maximal pour l’inclusion, alors on a
est un sous-groupe commutatif de GLn(K), maximal pour l’inclusion, alors on a
 = K[
= K[ ]× . Il suit de cela que les sous-groupes commutatifs maximaux de GLn(K) sont les
groupes des inversibles des sous-algèbres commutatives de
]× . Il suit de cela que les sous-groupes commutatifs maximaux de GLn(K) sont les
groupes des inversibles des sous-algèbres commutatives de  n(K) qui sont maximales pour
l’inclusion.
n(K) qui sont maximales pour
l’inclusion.
Corollaire 3. — Soit  un sous-groupe commutatif, maximal de GLn(K) ; on dispose alors de
l’inégalité dim K[
un sous-groupe commutatif, maximal de GLn(K) ; on dispose alors de
l’inégalité dim K[ ] ≤ 1 + α(n).
] ≤ 1 + α(n).
Soit n ≥ 4 et  un sous-groupe commutatif et maximal dans GLn(K). On suppose que
dimK[
un sous-groupe commutatif et maximal dans GLn(K). On suppose que
dimK[ ] = 1 + α(n). Alors il existe P
] = 1 + α(n). Alors il existe P  GLn(K) avec P
GLn(K) avec P P-1 = K×In ⊕
P-1 = K×In ⊕ si n est pair et
P
si n est pair et
P P-1 = K× In ⊕
P-1 = K× In ⊕ 1 ou P
1 ou P P-1 = K×In ⊕
P-1 = K×In ⊕ 2 si n est impair ; les espaces
2 si n est impair ; les espaces  ,
,  1,
1,  2
sont définis au théorème 1.
2
sont définis au théorème 1.
Démonstration C’est une conséquence immédiate des théorèmes 3 et 4, et du fait que
(KIn ⊕  )× = K×In ⊕
)× = K×In ⊕ et aussi (KIn ⊕
et aussi (KIn ⊕ i)× = K×In ⊕
i)× = K×In ⊕ i pour i = 1,2.
cqfd
i pour i = 1,2.
cqfd
Définition 2. — Soit  ⊂ GLn(K) un groupe commutatif constitué d’éléments unipotents, i.e.
⊂ GLn(K) un groupe commutatif constitué d’éléments unipotents, i.e.
 = In +
= In +  où
où  est constitué de nilpotents, on dira que
est constitué de nilpotents, on dira que  est un sous-groupe commutatif
unipotent de GLn(K). On appelle dimension de
est un sous-groupe commutatif
unipotent de GLn(K). On appelle dimension de  , la dimension du sous-espace vectoriel engendré
par
, la dimension du sous-espace vectoriel engendré
par  et on la note dim
et on la note dim ; on remarquera bien que si K≠F2,
; on remarquera bien que si K≠F2,  n’est pas un sous-groupe
commutatif, maximal de GLn(K).
n’est pas un sous-groupe
commutatif, maximal de GLn(K).
Proposition 3. — Soit  = In +
= In +  un sous-groupe commutatif, unipotent de GLn(K). Les
propriétés suivantes sont équivalentes.
un sous-groupe commutatif, unipotent de GLn(K). Les
propriétés suivantes sont équivalentes.
(i) Le groupe  est un sous-groupe de GLn(K) qui est maximal dans la famille des sous-groupes
commutatifs, unipotents de GLn(K) ;
est un sous-groupe de GLn(K) qui est maximal dans la famille des sous-groupes
commutatifs, unipotents de GLn(K) ;
(ii) l’ensemble  est un sous-espace vectoriel qui est maximal dans l’ensemble des sous-espaces
vectoriels de
est un sous-espace vectoriel qui est maximal dans l’ensemble des sous-espaces
vectoriels de  n (K) qui sont commutatifs et constitués de nilpotents.
n (K) qui sont commutatifs et constitués de nilpotents.
Démonstration ∙ Montrons que (i) implique (ii). On a  = In +
= In +  . Ensuite
. Ensuite  est une partie
commutative, en effet si A = In + N et Aʹ = In + Nʹ, alors AAʹ = AʹA implique facilement que
NNʹ = Nʹ N ; en conséquence le sous-espace vectoriel de
est une partie
commutative, en effet si A = In + N et Aʹ = In + Nʹ, alors AAʹ = AʹA implique facilement que
NNʹ = Nʹ N ; en conséquence le sous-espace vectoriel de  n(K) engendré par
n(K) engendré par  est
commutatif, facilement
est
commutatif, facilement  est une partie commutative, constituée de nilpotents. Alors il existe un
sous-espace vectoriel
est une partie commutative, constituée de nilpotents. Alors il existe un
sous-espace vectoriel  ʹ⊃
ʹ⊃ qui est maximal dans l’ensemble des sous-espaces vectoriels de
qui est maximal dans l’ensemble des sous-espaces vectoriels de
 n (K) qui sont commutatifs et constitués de nilpotents. Il suit de la proposition 1,
partie 2, que pour tout A,B
n (K) qui sont commutatifs et constitués de nilpotents. Il suit de la proposition 1,
partie 2, que pour tout A,B  V , on a AB
V , on a AB  V ; cela implique que In +
V ; cela implique que In +  ʹ est un
sous-groupe commutatif, unipotent. Comme
ʹ est un
sous-groupe commutatif, unipotent. Comme  est maximal, on a
est maximal, on a  =
=  ʹ, ce qui montre
(ii).
ʹ, ce qui montre
(ii).
∙ Montrons que (ii) implique (i). Comme  est un sous-espace vectoriel qui est maximal dans
l’ensemble des sous-espaces vectoriels de
est un sous-espace vectoriel qui est maximal dans
l’ensemble des sous-espaces vectoriels de  n(K) qui sont commutatifs et constitués de nilpotents,
il suit de la proposition 1, partie 2, que pour tout A,B
n(K) qui sont commutatifs et constitués de nilpotents,
il suit de la proposition 1, partie 2, que pour tout A,B 
 , on a AB
, on a AB 
 ; ainsi
; ainsi  = In +
= In +  est
un sous-groupe commutatif, unipotent de GLn(K) et comme
est
un sous-groupe commutatif, unipotent de GLn(K) et comme  est maximal, il suit que
est maximal, il suit que  est
maximal. cqfd
est
maximal. cqfd
Corollaire 4. — Soit  un sous-groupe commutatif de GLn(K), constitué d’éléments unipotents,
i.e. d’éléments de la forme In + N où N est nilpotent. Alors on a dim
un sous-groupe commutatif de GLn(K), constitué d’éléments unipotents,
i.e. d’éléments de la forme In + N où N est nilpotent. Alors on a dim ≤ α(n).
≤ α(n).
Soit n ≥ 4 et  un sous-groupe de GLn(K) qui est maximal dans l’ensemble des sous-groupes
commutatifs, unipotents de GLn(K), avec dim
un sous-groupe de GLn(K) qui est maximal dans l’ensemble des sous-groupes
commutatifs, unipotents de GLn(K), avec dim = α(n).
= α(n).
Alors il existe P  GLn(K) avec P
GLn(K) avec P P-1 = In +
P-1 = In +  si n est pair et P
si n est pair et P P-1 = In +
P-1 = In +  1 ou
P
1 ou
P P-1 = In +
P-1 = In +  2 si n est impair ;
2 si n est impair ;  ,
,  1,
1,  2 sont définis au théorème 1.
2 sont définis au théorème 1.
Démonstration Pour la première partie, on a donc  = In +
= In +  , ensuite
, ensuite  est une partie
commutative, en effet si A = In + N et Aʹ = In + Nʹ, alors AAʹ = AʹA implique facilement que
NNʹ = Nʹ N ; en conséquence le sous-espace vectoriel de
est une partie
commutative, en effet si A = In + N et Aʹ = In + Nʹ, alors AAʹ = AʹA implique facilement que
NNʹ = Nʹ N ; en conséquence le sous-espace vectoriel de  n(K) engendré par
n(K) engendré par  est
commutatif, le reste est conséquence du corollaire 1.
est
commutatif, le reste est conséquence du corollaire 1.
Pour la seconde partie, comme  = In +
= In +  est maximal, il suit de la proposition 2 que
est maximal, il suit de la proposition 2 que  est un
sous-espace vectoriel commutatif, constitué d’éléments nilpotents et de dimension α(n) puisque
dim
est un
sous-espace vectoriel commutatif, constitué d’éléments nilpotents et de dimension α(n) puisque
dim = α(n). Sachant que pour tout N
= α(n). Sachant que pour tout N 
 , on a χN(X) = Xn, il suit de la proposition 4 de
l’appendice qu’il existe P
, on a χN(X) = Xn, il suit de la proposition 4 de
l’appendice qu’il existe P  GLn(K) avec P
GLn(K) avec P P-1 ⊂ Tn,0(K). Le reste est conséquence du
théorème 2. cqfd
P-1 ⊂ Tn,0(K). Le reste est conséquence du
théorème 2. cqfd
Proposition 4. — Soient E un K-espace vectoriel de dimension finie, dimE = n ≥ 1,  une
famille commutative d’endomorphismes de E, i.e. pour tout u,v
une
famille commutative d’endomorphismes de E, i.e. pour tout u,v 
 , on a uv = vu. On suppose en
plus que pour tout u
, on a uv = vu. On suppose en
plus que pour tout u 
 , le polynôme caractéristique χu(X) se factorise en polynômes de degré 1
de K[X]. Alors E admet une décomposition E = E1 ⊕ E2 ⊕
, le polynôme caractéristique χu(X) se factorise en polynômes de degré 1
de K[X]. Alors E admet une décomposition E = E1 ⊕ E2 ⊕ ⊕ Es avec les propriétés qui
suivent.
⊕ Es avec les propriétés qui
suivent.
(1) Les Ei sont des sous-espaces vectoriels avec dimEi = ni ≥ 1.
(2) On a u(Ei ) ⊂ Ei pour tout u 
 . On note ui l’endomorphisme de Ei induit par u, alors
χui (X) = (X - λ(ui))ni où λ(ui)
. On note ui l’endomorphisme de Ei induit par u, alors
χui (X) = (X - λ(ui))ni où λ(ui)  K.
K.
(3) Il existe une base  i de Ei telle que Mat(ui,
i de Ei telle que Mat(ui, i) = λ(ui)Ini + Ni où Ni est une matrice
triangulaire supérieure de diagonale nulle.
i) = λ(ui)Ini + Ni où Ni est une matrice
triangulaire supérieure de diagonale nulle.
(4) Soit  i := {ui ; u
i := {ui ; u 
 }, alors
}, alors  i est une famille commutative. Si
i est une famille commutative. Si  est en plus, un sous-espace
vectoriel de End E (resp. une sous-algèbre de EndE, un sous-groupe de GL(E), un sous-groupe
unipotent de GL (E)), alors
est en plus, un sous-espace
vectoriel de End E (resp. une sous-algèbre de EndE, un sous-groupe de GL(E), un sous-groupe
unipotent de GL (E)), alors  i est en plus, un sous-espace vectoriel de EndEi (resp.
une sous-algèbre de EndEi, un sous-groupe de GL(Ei), un sous-groupe unipotent de
GL(Ei )).
i est en plus, un sous-espace vectoriel de EndEi (resp.
une sous-algèbre de EndEi, un sous-groupe de GL(Ei), un sous-groupe unipotent de
GL(Ei )).
La version matricielle de la proposition est la suivante
Soit  une famille commutative de matrices de
une famille commutative de matrices de  n(K), i.e. pour tout U,V
n(K), i.e. pour tout U,V 
 , on a UV = V U.
On suppose en plus que pour tout U
, on a UV = V U.
On suppose en plus que pour tout U 
 , le polynôme caractéristique χU(X) se factorise en
polynômes de degré 1 de K[X]. Alors il existe P
, le polynôme caractéristique χU(X) se factorise en
polynômes de degré 1 de K[X]. Alors il existe P  GLn(K) avec les propriétés qui
suivent.
GLn(K) avec les propriétés qui
suivent.
(1) Pour tout U 
 , l’élément PUP-1 est un tableau diagonal de matrices (U1,U2,…,Us) avec
Ui
, l’élément PUP-1 est un tableau diagonal de matrices (U1,U2,…,Us) avec
Ui 
 ni (K), 1 ≤ n1 ≤ n2 ≤
ni (K), 1 ≤ n1 ≤ n2 ≤ ≤ ns et n = n1 + n2 +
≤ ns et n = n1 + n2 +  + ns.
+ ns.
(2) On a χUi (X) = (X -λ(Ui))ni où λ(Ui)  K et Ui = λ(Ui)In
i + Ni où Ni est une matrice
triangulaire supérieure de diagonale nulle.
K et Ui = λ(Ui)In
i + Ni où Ni est une matrice
triangulaire supérieure de diagonale nulle.
(3) Soit  i := {Ui ; U
i := {Ui ; U 
 }, alors
}, alors  i est une famille commutative de
i est une famille commutative de  ni(K). Si
ni(K). Si  est en plus,
un sous-espace vectoriel de
est en plus,
un sous-espace vectoriel de  n(K) (resp. une sous-algèbre de
n(K) (resp. une sous-algèbre de  n(K), un sous-groupe de
GLn(K), un sous-groupe unipotent de GLn(K)), alors
n(K), un sous-groupe de
GLn(K), un sous-groupe unipotent de GLn(K)), alors  i est en plus, un sous-espace vectoriel de
i est en plus, un sous-espace vectoriel de
 ni (K) (resp. une sous-algèbre de
ni (K) (resp. une sous-algèbre de  ni(K), un sous-groupe de GLni(K), un sous-groupe
unipotent de GL ni(K)).
ni(K), un sous-groupe de GLni(K), un sous-groupe
unipotent de GL ni(K)).
(4) Dans le cas particulier où pour tout A 
 , le polynôme caractéristique de A est de la forme
χA (X) = (X - λ(A))n avec λ(A)
, le polynôme caractéristique de A est de la forme
χA (X) = (X - λ(A))n avec λ(A)  K, alors il existe P
K, alors il existe P  GLn(K) tel que P
GLn(K) tel que P P-1 ⊂ KIn ⊕
P-1 ⊂ KIn ⊕ où
où  ⊂ T n,0 (K).
⊂ T n,0 (K).
Démonstration
∙ On suppose que pour tout u 
 on a χu(X) = (X - λ(u))n avec λ(u)
on a χu(X) = (X - λ(u))n avec λ(u)  K. Alors on a
u = λ(u)IdE + nu où nu est nilpotent. Sachant que nu (resp. nv) est un polynôme en u (resp. v),
alors pour tout u, v
K. Alors on a
u = λ(u)IdE + nu où nu est nilpotent. Sachant que nu (resp. nv) est un polynôme en u (resp. v),
alors pour tout u, v 
 on a nunv = nvnu. On sait alors qu’il existe une base (e1,e2,…,en) de E
dans laquelle la matrice de tous les nu est triangulaire supérieure avec une diagonale nulle ( ex.
5.7.15 p. 237). Dans ce cas, la proposition est démontrée.
on a nunv = nvnu. On sait alors qu’il existe une base (e1,e2,…,en) de E
dans laquelle la matrice de tous les nu est triangulaire supérieure avec une diagonale nulle ( ex.
5.7.15 p. 237). Dans ce cas, la proposition est démontrée.
∙ On suppose qu’il existe u 
 avec χu(X) = (X -λ1)n1(X -λ2)n2
avec χu(X) = (X -λ1)n1(X -λ2)n2 (X -λr)nr, où λi
(X -λr)nr, où λi  K,
λi ≠ λj si i ⁄= j, r ≥ 2 et ni ≥ 1 pour i
K,
λi ≠ λj si i ⁄= j, r ≥ 2 et ni ≥ 1 pour i  {1,…,r}. Introduisons F1 := Ker(u - λ1IdE)n1 ainsi
que F2 = Ker (u - λ2IdE)n2 ⊕ ... ⊕ Ker(u - λrIdE)nr. Alors, on a E = F1 ⊕ F2 et
1 ≤ dim Fi < n.
{1,…,r}. Introduisons F1 := Ker(u - λ1IdE)n1 ainsi
que F2 = Ker (u - λ2IdE)n2 ⊕ ... ⊕ Ker(u - λrIdE)nr. Alors, on a E = F1 ⊕ F2 et
1 ≤ dim Fi < n.
Il suit de la commutativité que pour tout v 
 , on a v(F1) ⊂ F1 et v(F2) ⊂ F2. Soit vi
l’endomorphisme de Fi induit par v et
, on a v(F1) ⊂ F1 et v(F2) ⊂ F2. Soit vi
l’endomorphisme de Fi induit par v et  i := {vi | v
i := {vi | v 
 }. Facilement
}. Facilement  i satisfait les hypothèses
du théorème pour Fi.
i satisfait les hypothèses
du théorème pour Fi.
Par récurrence sur la dimension, on a une décomposition F1 = E1 ⊕ E2 ⊕ ⊕ Et qui satisfait
aux conclusions du théorème pour
⊕ Et qui satisfait
aux conclusions du théorème pour  1 ; de même, on a une décomposition
1 ; de même, on a une décomposition
 2. Il suit facilement que la décomposition
E = E1 ⊕ E2 ⊕
2. Il suit facilement que la décomposition
E = E1 ⊕ E2 ⊕  ⊕ Es satisfait aux conclusions du théorème. cqfd
⊕ Es satisfait aux conclusions du théorème. cqfd
Dans ce qui suit  s,t(K) désigne la K-algèbre des matrices à s lignes et t colonnes.
s,t(K) désigne la K-algèbre des matrices à s lignes et t colonnes.
Soit (a, b, c, d, e, f,g,h)  K8 et
K8 et
![[ 0 0 a 0 b 0 c e 0 f 0 g ]
W1=W1(a,b,c,d,e,f,g,h) := 0 0 0 a 0 b d 0 e 0 f h ∈ M2,12(K ).](/numeros/RMS130-4/RMS130-4109x.png)
Soit (m, n, p, q)  K4 et W2 = W2(m,n,p,q) :=
K4 et W2 = W2(m,n,p,q) := ![[ ]
m n
p q](/numeros/RMS130-4/RMS130-4110x.png)

 2,2(K). Soit W3
la matrice nulle de
2,2(K). Soit W3
la matrice nulle de  12,12(K) et W4 = W4(a,b,c,d,e,f,g,h)
12,12(K) et W4 = W4(a,b,c,d,e,f,g,h) 
 12,2(K) défini
par
12,2(K) défini
par
![t[ c d 0 0 a g h 0 0 e 0 0 ]
W4= 0 0 c d b 0 0 g h f 0 0 ∈ M2,12(K ).](/numeros/RMS130-4/RMS130-4111x.png)
Soit
![[ W1 W2 ]
W = W (a,b,c,d,e,f,g,h,m,n,p,q) := W3 W4 .](/numeros/RMS130-4/RMS130-4112x.png)
Enfin soit
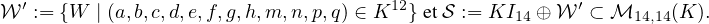
Facilement  est un sous-espace vectoriel de
est un sous-espace vectoriel de  14,14(K) de dimension 13. Assez facilement
14,14(K) de dimension 13. Assez facilement  est
une sous-algèbre commutative de
est
une sous-algèbre commutative de  14,14(K). Plus difficilement Courter montre que
14,14(K). Plus difficilement Courter montre que  est une
sous-algèbre commutative maximale de
est une
sous-algèbre commutative maximale de  14,14(K).
14,14(K).
Remerciements.
Nous remercions le relecteur pour ses remarques judicieuses.
Références
[Co1] Courter R. C. The maximum dimension of nilpotent subspaces of Kn satisfying the identity Sd. Journal of Algebra, 91, 82-110 (1984)
[Co2] Courter R. C. The dimension of maximal commutative subalgebras of Kn. Duke Math. J. 225-232 (1965)
[Cow] Cowsik R. C. A short note on the Schur-Jacobson theorem. Proceedings of the American Mathematical Society vol. 118, no2, 675-676, juin 1993
[F1] Fresnel J. Algèbre des matrices. Hermann (2011)
[F2] Fresnel J. Espaces quadratiques, euclidiens, hermitiens. Hermann (1999)
[F-M1] Fresnel J., Matignon M. Algèbre et Géométrie, recueil d’exercices corrigés.
Hermann (2011) et
Errata https ://www.math.u-bordeaux.fr/~mmatigno/agregation.html
[F-M2] Fresnel J., Matignon M. Algèbre et Géométrie, 81 thèmes pour l’agrégation de
mathématiques. Ellipses (2017) et
Compléments-Errata https ://www.math.u-bordeaux.fr/~mmatigno/agregation.html
[G] Gustafson W. H. On maximal commutative algebras of linear transformations. Journal of Algebra 42, 557-563 (1976)
[J] Jacobson N. Schur’s theorems on commutative matrices. Bull. Amer. Math. Soc. 50, 431-436 (1944)
[K] Karamzadeh N. S. Schur’s inequality for the dimension of commuting families of matrices. Inequalities & Applications, vol. 13 no3, 625-628 (2010)
[M] Mirzakhani M. A simple proof of a theorem of Schur, The American Mathematical Monthly, vol. 105, no3, 260-262 (mars 1998)
[S] Schur I. Zur Theorie der vertauschbaren Matrizen. J. Reine Angew. Math. 130, 66-76 (1905)
[Table des matières]

