[Table des matières]
Du côté des élèves
de Terminale S
Questions proposées aux élèves de Terminale S
1. Démontrer qu’il existe une infinité de triplets d’entiers naturels consécutifs, s’écrivant chacun comme somme de deux carrés.
2. Déterminer l’ensemble des fonctions f : R-→R, continues vérifiant pour tout (x,y)  R2 tel
que x≠ y :
R2 tel
que x≠ y :
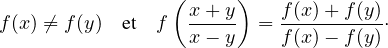
3. Soient ABC un triangle, G son centre de gravité et I le centre du cercle inscrit à ABC. On note a,b,c les longueurs respectives des côtés [BC],[CA] et [AB]. On suppose I ⁄ G. Montrer que (IG) est perpendiculaire à la bissectrice (IC)si et seulement si la moyenne arithmétique de a,b,c est égale à la moyenne harmonique de a et b. Qu’en est-il si I = G?
4. Soit M une matrice carrée de taille n à coefficients entiers inversible telle que M-1 est aussi à coefficients entiers. On note N le nombre de coefficients impairs de M.
a) Montrer que : n ≤ N ≤ n2 - n + 1.
b) Cet encadrement est-il optimal ?
Problème : combinatoire et probabilités
Soit n  N \
N \ 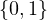 . On note
. On note  n l’ensemble des permutations de
n l’ensemble des permutations de ![[[1,n]]](/numeros/RMS130-4/RMS130-4948x.png) . On observe la position
initiale de n personnes rangées en ligne puis on effectue une permutation aléatoire de ces n
personnes. Pour k
. On observe la position
initiale de n personnes rangées en ligne puis on effectue une permutation aléatoire de ces n
personnes. Pour k 
![[[0,n - 1]]](/numeros/RMS130-4/RMS130-4949x.png) , on note En,k l’événement ≪k des n- 1 paires de voisins initiaux
se retrouvent comme paires de voisins dans la disposition finale ≫. Soit A(n,k) le cardinal de En,k,
considéré comme le sous-ensemble de Ω =
, on note En,k l’événement ≪k des n- 1 paires de voisins initiaux
se retrouvent comme paires de voisins dans la disposition finale ≫. Soit A(n,k) le cardinal de En,k,
considéré comme le sous-ensemble de Ω =  n formé des permutations σ
n formé des permutations σ 
 n pour lesquelles
exactement k valeurs de i
n pour lesquelles
exactement k valeurs de i 
![[[1,n- 1]]](/numeros/RMS130-4/RMS130-4950x.png) sont telles que i et i + 1 sont consécutifs dans n’importe
quel ordre dans la liste σ(1),σ(2),…,σ(n). Le but de ce problème est de déterminer ℙ
sont telles que i et i + 1 sont consécutifs dans n’importe
quel ordre dans la liste σ(1),σ(2),…,σ(n). Le but de ce problème est de déterminer ℙ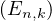 et de
montrer que lim n→+∞ℙ
et de
montrer que lim n→+∞ℙ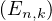 =
= 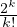 e-2.
e-2.
La partie I présente des résultats préliminaires de combinatoire et d’analyse appliqués dans la partie II qui traite le problème proprement dit.
Dans tout le problème, on note pour m  N* et l
N* et l 
![[[0,m ]]](/numeros/RMS130-4/RMS130-4954x.png) ,
, 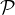 l
l![([[1,m ]])](/numeros/RMS130-4/RMS130-4955x.png) , l’ensemble des parties de
, l’ensemble des parties de
![[[1,m]]](/numeros/RMS130-4/RMS130-4956x.png) de cardinal l.
de cardinal l.
1. Soient m, n, r des entiers naturels. Démontrer la formule dite de Vandermonde :
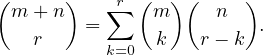
2. Soient n, p  N*. On note
N*. On note  p,n l’ensemble des applications strictement croissantes de
p,n l’ensemble des applications strictement croissantes de ![[[1,p]]](/numeros/RMS130-4/RMS130-4958x.png) dans
dans ![[[1,n]]](/numeros/RMS130-4/RMS130-4959x.png) et
et 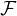 p,n l’ensemble des (x1,…,xp)
p,n l’ensemble des (x1,…,xp) 
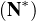 p tels que x
1 + x2 +
p tels que x
1 + x2 +  + xp = n.
+ xp = n.
a) Montrer que card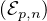 =
=  .
.
b) Établir une bijection de 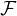 p,n dans
p,n dans  p-1,n-1 et en déduire que card
p-1,n-1 et en déduire que card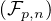 =
= 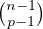 .
.
3. Cette question propose un résultat fondé sur le principe d’inclusion-exclusion. Soit E un
ensemble de cardinal N  N*. On suppose les éléments de E classés selon r propriétés notées
α1 , … , αr . Soit B ⊂
N*. On suppose les éléments de E classés selon r propriétés notées
α1 , … , αr . Soit B ⊂![[[1,r]]](/numeros/RMS130-4/RMS130-4966x.png) ; on note N(B) le nombre d’éléments de E vérifiant les propriétés αj
pour j
; on note N(B) le nombre d’éléments de E vérifiant les propriétés αj
pour j  B. Si B = ∅, N(∅) = N ; on pose pour tout l
B. Si B = ∅, N(∅) = N ; on pose pour tout l 
![[[0,r]]](/numeros/RMS130-4/RMS130-4967x.png) :
:
sl = ![∑
B⊂Pl([[1,r]])](/numeros/RMS130-4/RMS130-4968x.png) N(B). De façon plus détaillée on a :
N(B). De façon plus détaillée on a :
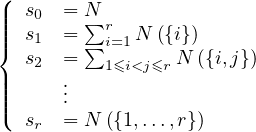
Pour B ⊂ ![[[1,r]]](/numeros/RMS130-4/RMS130-4970x.png) , on note ν(B) le nombre d’éléments de E vérifiant les propriétés αj
pour j
, on note ν(B) le nombre d’éléments de E vérifiant les propriétés αj
pour j  B et aucune des propriétés αj pour j
B et aucune des propriétés αj pour j  B =
B = ![[[1,r]]](/numeros/RMS130-4/RMS130-4971x.png) \ B. Pour l
\ B. Pour l 
![[[0,r]]](/numeros/RMS130-4/RMS130-4972x.png) , on
pose :
, on
pose :
eℓ = ![∑
B∈P ℓ([[1,r]])](/numeros/RMS130-4/RMS130-4973x.png) ν(B). ν(B).
|
Remarquer que el est le nombre d’éléments de E vérifiant exactement l des propriétés α1,…,αr et démontrer que
![r-m ( )
∀m ∈ [[0,r]],em = ∑ (- 1)j m + j sm+j
j=0 j](/numeros/RMS130-4/RMS130-4974x.png) | (*) |
Ind. Considérer x  E et étudier combien de fois est compté x dans le membre de droite de
(*) selon le nombre de propriétés α1,…,αr qu’il vérifie exactement. On remarquera
que :
E et étudier combien de fois est compté x dans le membre de droite de
(*) selon le nombre de propriétés α1,…,αr qu’il vérifie exactement. On remarquera
que :
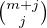
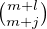 =
= 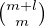
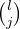 .
.
4. a) Montrer que pour tout x  R et tout n
R et tout n  N,
N,
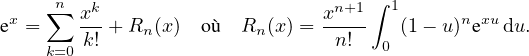
b) Montrer que : ∀n  N, ∀x
N, ∀x  R, |Rn(x)|≤
R, |Rn(x)|≤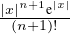 ⋅
⋅
c) En déduire que pour tout x  R, ex = limn→+∞
R, ex = limn→+∞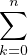
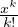 ⋅
⋅
5. 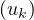 k
k N étant une suite réelle, on s’intéresse à la série de terme général uk, c’est-à-dire à la
suite n
N étant une suite réelle, on s’intéresse à la série de terme général uk, c’est-à-dire à la
suite n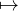
 uk. On dit que la série de terme général uk converge si et seulement si la suite
n
uk. On dit que la série de terme général uk converge si et seulement si la suite
n
 uk converge ; dans ce cas, la limite de cette suite est appelée somme de la série et notée
uk converge ; dans ce cas, la limite de cette suite est appelée somme de la série et notée
 uk .
uk .
Soit (ak ) une suite d’applications de N dans R. On suppose que pour tout k  N, la suite n
N, la suite n ak(n)
converge et a pour limite λk et qu’il existe α : N-→R+, telle que :
ak(n)
converge et a pour limite λk et qu’il existe α : N-→R+, telle que :
- ∀k
 N , ∀n
N , ∀n  N, |ak(n)|≤ α(k),
N, |ak(n)|≤ α(k),
- la série de terme général α(k) converge,
a)
∙ Montrer que pour tout n  N, la série de terme général
N, la série de terme général 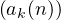 k
k N est convergente.
N est convergente.
On note S(n) = limN→+∞ ak(n) =
ak(n) =  ak(n), la somme de cette série.
ak(n), la somme de cette série.
∙ Montrer que la série de terme général λk est convergente.
b) Montrer que limn→+∞S(n) =  λk, autrement dit que :
λk, autrement dit que :
limn→+∞ ak(n) = ak(n) =  limn→+∞ak(n). limn→+∞ak(n).
|
Ind. Considérer n0  N tel que ∀k > n0,
N tel que ∀k > n0, 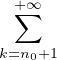 α(k) <
α(k) < 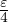 et remarquer que :
et remarquer que :
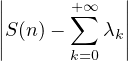 ≤ ≤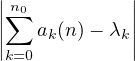 + 2 + 2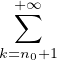 α(k) < α(k) < 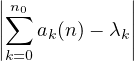 + + 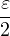 ⋅ ⋅
|
On reprend la question posée dans l’introduction ainsi que les notations. Pour i 
![[[1,n - 1]]](/numeros/RMS130-4/RMS130-41003x.png) , on
note Ai l’ensemble des σ
, on
note Ai l’ensemble des σ 
 n tels que i et i + 1 sont deux termes consécutifs dans n’importe quel
ordre dans la liste σ(1),σ(2),…,σ(n) et l’on pose :
n tels que i et i + 1 sont deux termes consécutifs dans n’importe quel
ordre dans la liste σ(1),σ(2),…,σ(n) et l’on pose :
si = ![∑
B∈Pi([[1,n-1]])](/numeros/RMS130-4/RMS130-41004x.png) card
card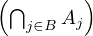 et l’on convient que s0 = n!.
et l’on convient que s0 = n!.
1. Montrer en appliquant I-3 que :
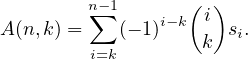
2. Cette question a pour but de déterminer si.
a) Soit B 
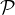 i (
i (![[[1,n]]](/numeros/RMS130-4/RMS130-41007x.png) ) où i
) où i 
![[[1,n- 1]]](/numeros/RMS130-4/RMS130-41008x.png) . On appelle composante de B tout sous-ensemble de B formé d’entiers
consécutifs maximal7
pour l’inclusion. On suppose que B possède c composantes. Montrer que :
. On appelle composante de B tout sous-ensemble de B formé d’entiers
consécutifs maximal7
pour l’inclusion. On suppose que B possède c composantes. Montrer que :
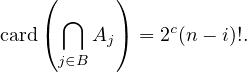
b) Pour m, i, c  N tels que n ≥ m ≥ i ≥ c, on note u(m,i,c) le nombre de sous-ensembles B de
N tels que n ≥ m ≥ i ≥ c, on note u(m,i,c) le nombre de sous-ensembles B de
![[[1,m]]](/numeros/RMS130-4/RMS130-41012x.png) de cardinal i ayant c composantes. Montrer que :
de cardinal i ayant c composantes. Montrer que :
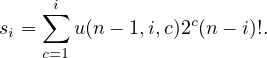
3. Soient m, i, c  N* tels que n ≥ m ≥ i ≥ c.
N* tels que n ≥ m ≥ i ≥ c.
a) ∙ Montrer que tout B 
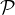 i
i![([[1,m ]])](/numeros/RMS130-4/RMS130-41014x.png) ayant c composantes est déterminé par la donnée du
(2c + 1)-uplet d’entiers naturels (j0,i1,j1,i2,j2,…,ic,jc) où i1,i2,…,ic sont les cardinaux des
composantes de B dans l’ordre où on les trouve, où pour l
ayant c composantes est déterminé par la donnée du
(2c + 1)-uplet d’entiers naturels (j0,i1,j1,i2,j2,…,ic,jc) où i1,i2,…,ic sont les cardinaux des
composantes de B dans l’ordre où on les trouve, où pour l 
![[[1,c - 1]]](/numeros/RMS130-4/RMS130-41015x.png) , jl est le nombre d’entiers
séparant les composantes de B de rang l et l + 1, j0 est le nombre d’éléments de
, jl est le nombre d’entiers
séparant les composantes de B de rang l et l + 1, j0 est le nombre d’éléments de ![[[1,m]]](/numeros/RMS130-4/RMS130-41016x.png) strictement inférieur à minB et jc est le nombre d’éléments de
strictement inférieur à minB et jc est le nombre d’éléments de ![[[1,m]]](/numeros/RMS130-4/RMS130-41017x.png) strictement supérieurs à
maxB.
strictement supérieurs à
maxB.
∙ Vérifier que, ∀l 
![[[1,c]]](/numeros/RMS130-4/RMS130-41018x.png) , il > 0 et i1 +
, il > 0 et i1 +  + il = i, que j0 ≥ 0, jc ≥ 0 et que
+ il = i, que j0 ≥ 0, jc ≥ 0 et que
∀l 
![[[1,c-1]]](/numeros/RMS130-4/RMS130-41020x.png) , jl > 0 et j0 + j1 +
, jl > 0 et j0 + j1 +  + jc = m - i
+ jc = m - i
b) En déduire en appliquant I-2 que u(m,i,c) = 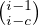
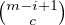 .
.
c) Montrer alors que :
![n∑-1[ ( ) ∑i ( )( ) ]
A(n,k) = (- 1)i- k i i- 1 n- i 2c(n- i)! .
i=k k c=1 i- c c](/numeros/RMS130-4/RMS130-41024x.png)
4. On se propose de déterminer limn→+∞ℙ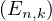 . Soit i
. Soit i  N tel que i ≥ k. On pose :
N tel que i ≥ k. On pose :
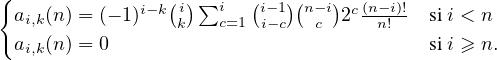
a) Vérifier que ℙ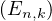 =
= 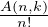 =
= 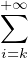 aik(n).
aik(n).
b) Montrer que |ai,k(n)|≤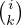 2i
2i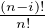
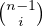 , puis que |ai,k(n)|≤
, puis que |ai,k(n)|≤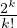
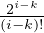 ⋅
⋅
c) Montrer que limn→+∞aik(n) = 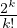 (-1)i-k
(-1)i-k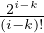 ⋅
⋅
d) En appliquant I-5, montrer que limn→+∞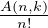 =
= 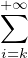
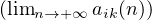 .
.
e) En déduire que :
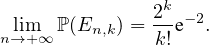
5. Soit Xn la variable aléatoire indiquant le nombre de paires de personnes
initialement voisines qui demeurent voisines après une perturbation aléatoire. On a
montré8 en
4.e) que lim n→+∞ℙ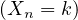 =
= 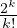 e-2⋅
e-2⋅
a) Calculer E(Xn), l’espérance de Xn.
Solution de la question 2 proposée dans la RMS 129-1
Texte de la question 2. Soient a et b deux réels tels que a < b et f : [a,b]-→R, une fonction
continue sur [a, b] et dérivable sur ![]a,b[](/numeros/RMS130-4/RMS130-41044x.png) telle que f(a) = f(b) = 0.
telle que f(a) = f(b) = 0.
Montrer que pour tout réel r, il existe c 
![]a,b[](/numeros/RMS130-4/RMS130-41045x.png) tel que fʹ(c) = r
tel que fʹ(c) = r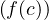 2.
2.
Solution. Soient r  R et F : [a,b]-→R, x
R et F : [a,b]-→R, x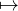
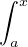 f(t)d t, la primitive de f nulle en a et
g : [a, b]-→ R , x
f(t)d t, la primitive de f nulle en a et
g : [a, b]-→ R , x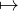 e-rF(x)f(x).
e-rF(x)f(x).
- les hypothèses sur f assurent que g est continue sur [a,b] et dérivable sur
![]a,b[](/numeros/RMS130-4/RMS130-41050x.png) .
.
- g(a) = g(b) = 0 car f(a) = f(b) = 0.
La fonction g vérifiant les hypothèses du théorème de Rolle, il existe c 
![]a,b[](/numeros/RMS130-4/RMS130-41051x.png) tel que gʹ(c) = 0.
Or,
tel que gʹ(c) = 0.
Or,
∀x  ![]a,b[](/numeros/RMS130-4/RMS130-41052x.png) , gʹ(x) = e-rF(x) , gʹ(x) = e-rF(x)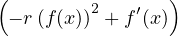 , ,
|
donc gʹ(c) = 0 si et seulement si fʹ(c) = r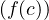 2.
2.
Ainsi, pour tout r  R, il existe c
R, il existe c 
![]a,b[](/numeros/RMS130-4/RMS130-41055x.png) tel que fʹ(c) = r
tel que fʹ(c) = r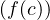 2.
2.
[Table des matières]

