[Questions-Reponses]
R937. Posé dans 127-3. Suite de R876 (RMS 127-3).
Existe-t-il f : I → R où I est un intervalle entourant 0, nulle en 0 et dérivable, vérifiant
f(x) 1 + fʹ(x)
1 + fʹ(x) = x2 pour tout x de I ? Si une telle fonction existe, est-elle deux fois
dérivable ? indéfiniment dérivable ? développable en série entière en 0 ?
(RMS)
= x2 pour tout x de I ? Si une telle fonction existe, est-elle deux fois
dérivable ? indéfiniment dérivable ? développable en série entière en 0 ?
(RMS)
Voici une réponse complète. Certaines preuves ont été modifiées par la rédaction avec l’accord de l’auteur.
Réponse de Jacques Henry
On note (E) l’équation différentielle
| y(yʹ + 1) = x2. |
On appelle solution de (E) un couple (I,φ) où I est un intervalle non trivial de R, φ : I → R dérivable et vérifiant
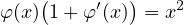 | (1) |
pour tout x de I. On montrera :
Théorème 1.Il existe une unique solution maximale f0 de (E) telle que f0(0) = 0 et que fʹ0 (0) = -1.
Elle est définie sur un intervalle ]α0,+∞[ où α0 est un réel strictement négatif. C’est la seule
solution maximale de (E) définie en 0 et analytique en 0. Plus précisément il existe une série
entière  n≥1unxn dont la somme est f0(x) sur ] - α0,α0[.
n≥1unxn dont la somme est f0(x) sur ] - α0,α0[.
Théorème 2.Il existe un ensemble infini Γ de solutions maximales g de (E) vérifiant
g(0) = 0 et gʹ(0) = 0. Chacune d’elles est définie sur un intervalle ]α,+∞[ où α0 < α < 0 ;
inversement tout α de ]α0,0[ est l’extrémité gauche de l’intervalle de définition d’un unique
élément de Γ. Elles sont toutes de classe 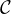 ∞ et aucune n’est analytique en 0. Elles coïncident
toutes sur [0, +∞[.
∞ et aucune n’est analytique en 0. Elles coïncident
toutes sur [0, +∞[.
On reprendra la question à ses débuts sans tenir compte des résultats obtenus dans la solution de l’exercice qui est à l’origine de la question.
1.1. Le problème de raccord
On note (E* ) l’équation différentielle yʹ = -1 + 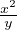 .
.
Une solution de (E*) ne s’annule pas ; elle est donc soit strictement positive soit strictement
négative. On notera  + (resp.
+ (resp.  -) l’ensemble des solutions maximales positives (resp. négatives)
de (E* ). Désormais on sous-entendra ≪ maximale ≫ quand on parlera de solution de (E*).
Par une récurrence immédiate, on montre que toute solution de (E*) est indéfiniment
dérivable.
-) l’ensemble des solutions maximales positives (resp. négatives)
de (E* ). Désormais on sous-entendra ≪ maximale ≫ quand on parlera de solution de (E*).
Par une récurrence immédiate, on montre que toute solution de (E*) est indéfiniment
dérivable.
Le théorème de Cauchy-Lipschitz s’applique à l’équation (E*) en tout point du plan privé de l’axe
des x. Pour tout point (x,y) tel que y≠0 il existe exactement un élément φ de  tel que φ(x) = y.
De plus l’intervalle de définition d’une solution de (E*) est ouvert. Voici un résultat fort utile pour
une solution φ de (E*).
tel que φ(x) = y.
De plus l’intervalle de définition d’une solution de (E*) est ouvert. Voici un résultat fort utile pour
une solution φ de (E*).
Proposition 1.Soit α une extrémité de l’intervalle de définition de φ que l’on suppose finie ; on suppose que φ admet en α une limite l. Alors l = 0 ou l = ±∞.
Démonstration.En effet d’après un corollaire du théorème de Cauchy-Lipschitz le point (α, l) ne peut pas appartenir à l’ouvert de définition de (E*) qui est donné par : y≠0. __
Une solution maximale f de l’équation (E) qui n’est pas solution de (E*) est définie sur un
intervalle I contenant 0 et est nulle en 0. Si I∩]0,+∞[ (resp. I∩] -∞,0[) n’est pas vide alors la
restriction φ de f à cet intervalle est une solution maximale de (E*) telle que la fonction φ (resp. ψ)
prolongée par φ(0) = 0 (resp. ψ(0) = 0) est dérivable en 0 avec φʹ(0) = fʹ(0) (resp.
ψʹ(0) = fʹ(0)).
Pour résoudre (E) on cherche donc les solutions de (E*) dont 0 est une des deux extrémités de l’intervalle de définition puis on étudie leur dérivabilité en 0 et on raccorde éventuellement une solution définie à gauche de 0 avec une solution définie à droite de 0.
1.2. Variations des solutions
Voici une propriété qui exprime le rapprochement des graphes dans le sens des x croissants.
Proposition 2.On considère φ1 et φ2, deux éléments distincts de  +, ou bien deux éléments
de
+, ou bien deux éléments
de  - . On suppose non vide l’intersection I de leurs ensembles de définition. Alors la
fonction d : I → R donnée par d(x) = |φ2(x) - φ1(x)| est strictement décroissante sur I.
- . On suppose non vide l’intersection I de leurs ensembles de définition. Alors la
fonction d : I → R donnée par d(x) = |φ2(x) - φ1(x)| est strictement décroissante sur I.
Démonstration.La fonction d ne s’annule pas sur I. On peut supposer φ1(x) < φ2(x) sur I.
Alors d = φ2 - φ1 est strictement positive et dʹ(x) = -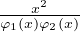 d(x) < 0 pour tout x de
I. Donc d décroît sur I. __
d(x) < 0 pour tout x de
I. Donc d décroît sur I. __
Soit φ un élément de  -. Alors φʹ < 0 (et même φʹ < -1). Donc φ est strictement décroissante.
-. Alors φʹ < 0 (et même φʹ < -1). Donc φ est strictement décroissante.
Pour étudier les variations des éléments de  + on aura besoin de la proposition suivante.
+ on aura besoin de la proposition suivante.
Proposition 3.Soit φ un élément de  + défini sur l’intervalle ouvert ]α,β[ où -∞≤ α <
β ≤ +∞. Alors la dérivée de φ s’annule au plus deux fois. De plus si elle s’annule en u < 0
alors φʹ > 0 sur ]α,u[ et φʹ < 0 sur ]u,min(0,β)[ et si elle s’annule en v > 0 alors φʹ < 0
sur ] max (0, α), v[ et φʹ > 0 sur ]v,β[.
+ défini sur l’intervalle ouvert ]α,β[ où -∞≤ α <
β ≤ +∞. Alors la dérivée de φ s’annule au plus deux fois. De plus si elle s’annule en u < 0
alors φʹ > 0 sur ]α,u[ et φʹ < 0 sur ]u,min(0,β)[ et si elle s’annule en v > 0 alors φʹ < 0
sur ] max (0, α), v[ et φʹ > 0 sur ]v,β[.
Démonstration.La dérivée seconde de φ vérifie :
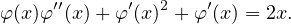 | (2) |
Soit x tel que φʹ(x) = 0, alors φ(x) = x2 et, d’après derpremiere, x n’est pas nul donc φʹʹ(x) = 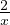 .
Si x < 0 (resp. x > 0) alors φʹʹ(x) < 0 (resp. φʹʹ(x) > 0) et, localement, φʹ est strictement
positive (resp. négative) à gauche de x et strictement négative (resp. positive) à droite de
x.
.
Si x < 0 (resp. x > 0) alors φʹʹ(x) < 0 (resp. φʹʹ(x) > 0) et, localement, φʹ est strictement
positive (resp. négative) à gauche de x et strictement négative (resp. positive) à droite de
x.
Ainsi les zéros de φʹ sont des points isolés et deux zéros consécutifs de φʹ ne peuvent être de même signe. Le reste s’en déduit aisément. __
Dans la suite, on considère une solution φ de (E*). On donne α et β les extrémités de son intervalle
de définition. Dans tous les cas φ est monotone au voisinage de α comme de β ; elle admet donc des
limites finies ou non : λ en α et μ en β.
Avant de décrire complètement les variations de φ suivant les cas, on établit quelques lemmes
utiles. Les preuves des trois premiers sont faites pour l’extrémité gauche mais conviennent tout
aussi bien pour l’extrémité droite.
Démonstration.Supposons par l’absurde que α soit -∞ et que λ soit fini. Alors, d’après la relation derpremiere, |φʹ(x)| tend vers +∞ quand x tend vers -∞. Il en résulte que la limite quand x tend vers -∞ de φ(x)⁄x est infinie donc λ est infini et il y a contradiction. __
Lemme 2.Si λ est fini (resp. μ est fini) alors α est fini (resp. β est fini) et λ = 0 (resp. μ = 0).
Démonstration.La première conclusion est une conséquence du lemme et la seconde de la proposition . __
Démonstration.Supposons par l’absurde que α soit fini et que λ soit infini alors d’après la relation derpremiere, φʹ(x) tend vers - 1 quand x tend vers α. La fonction φʹ est alors intégrable sur un certain intervalle ]α,x0] et φ admet donc une limite finie en α ; c’est contradictoire. __
Démonstration.Supposons par l’absurde α = -∞. Alors d’après le lemme on a λ = ±∞.
Si φ est négative alors φ est décroissante et 0 ≥ λ > -∞ ; c’est contradictoire.
Si φ est positive alors λ = +∞ et φ est décroissante sur un certain intervalle ] -∞,x0]. Donc pour tout x de cet intervalle on a d’après derpremiere, - 1 < φʹ(x) < 0 et φ(x) > x2. Il en résulte
x2 < φ(x) < x0 + φ(x0) - x.
Cet encadrement est impossible pour x suffisamment proche de -∞. Ainsi α > -∞. D’après le lemme , on a : λ = 0.
Il est clair que si φ est positive alors elle est croissante au voisinage de α. __
Lemme 5.Si φ est positive et si φʹ s’annule exactement une fois alors β = 0 et μ = 0. Sinon β = +∞ et μ = ±∞.
Démonstration.On passe en revue les différentes possibilités pour β :
1. Si β = +∞, d’après le lemme 1, μ = ±∞. On a alors deux cas.
- ou bien φ est positive : alors μ = +∞, φ est croissante au voisinage de + ∞ donc, d’après la proposition , φʹ ne s’annule pas ou s’annule exactement deux fois.
- ou bien φ est négative : alors μ = -∞ et φʹ est strictement négative donc ne s’annule
pas.
2. Si β < +∞ alors μ est fini et dans ce cas, d’après le lemme , μ = 0. C’est impossible si φ est
négative car elle serait alors strictement décroissante et on aurait μ < 0. De même φ ne peut pas
être positive et croissante au voisinage de β. Donc φ est décroissante et positive au voisinage de
β.
Comme elle est croissante au voisinage de α, la dérivée s’annule en un point u. D’après la proposition ce zéro u de φʹ est unique et négatif. Alors, pour tout x de ]u,β[ on a φʹ(x) < 0 donc φ(x) > x2 , d’où, par passage à la limite en β, 0 ≥ β2 donc β = 0. __
On peut maintenant préciser les variations des solutions.
On distingue pour le moment quatre types de solutions sous réserve d’existence.
- φ est négative.
Alors φ est définie sur ]α,+∞[ pour un certain réel α ; elle admet un prolongement continu, noté encore φ, à [α,+∞[, avec φ(α) = 0 ; elle décroît strictement de 0 à - ∞.
- φ est positive et φʹ ne s’annule pas.
Alors φ est définie sur ]α,+∞[ pour un certain réel α ≥ 0 ; elle admet un prolongement continu, noté encore φ, à [α,+∞[, avec φ(α) = 0 ; elle croît strictement de 0 à + ∞.
- φ est positive et φʹ s’annule exactement une fois.
Alors φ est définie sur ]α,0[ pour un certain réel α < 0 ; elle admet un prolongement continu, noté encore φ, à [α,0], avec φ(α) = 0 et φ(0) = 0 ; elle croît strictement de 0 à u2 puis décroît strictement de u2 à 0 pour un certain u tel que α < u < 0.
- φ est positive et φʹ s’annule exactement deux fois.
Alors φ est définie sur ]α,+∞[ pour un certain réel α < 0 ; elle admet un prolongement continu, noté encore φ, à [α,+∞[, avec φ(α) = 0 ; elle croît de 0 à u2 sur [α, u], pour un certain u de ]α,0[, décroît de u2 à v2 sur [u,v] pour un certain v > 0 puis croît de v2 à + ∞ sur [v,+∞[.
Démonstration.Si φ est positive et si φʹ ne s’annule pas alors 0 n’appartient pas l’intervalle de définition de φ car φ(x) < x2 pour tout x et comme β = +∞, nécessairement α ≥ 0. Le reste découle des cinq lemmes précédents. __
On notera désormais, pour 0 ≤ i ≤ 2, 
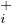 l’ensemble des solutions positives dont la dérivée
s’annule exactement i fois. L’ensemble
l’ensemble des solutions positives dont la dérivée
s’annule exactement i fois. L’ensemble 
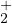 n’est pas vide car il contient toute solution φ dont le
graphe passe par (0,y) pour un certain y > 0.
n’est pas vide car il contient toute solution φ dont le
graphe passe par (0,y) pour un certain y > 0.
1.3. Les fonctions φα et ψα
Pour toute solution φ de (E*), notons A(φ) le réel α qui est l’extrémité gauche de l’intervalle de
définition de φ.
On établira, pour tout α réel, l’existence et l’unicité d’une solution positive φ et d’une solution
négative ψ telles que A(φ) = A(ψ) = α.
Soit deux solutions φ1 et φ2 de même signe et telles que A(φ1) = A(φ2). D’après la proposition
|φ2 - φ1 | décroît et a une limite nulle en A(φ1), donc φ2 = φ1. Ainsi il existe au plus une solution
φ > 0 telle que A(φ) = α ; on la note alors φα. Il existe au plus une solution ψ < 0 telle que
A(ψ) = α; on la note alors ψα.
Montrons maintenant l’existence de φα et ψα pour tout α non nul.
Notons (i, j) la base canonique de R2. Considérons le champ de vecteurs défini sur R2 par
| V(x,y) = yi + (x2 - y)j. |
Soit α un réel non nul. On peut appliquer le théorème de Cauchy-Lipschitz en (α,0) pour construire une courbe intégrale
t Φα (t) = Xα (t)i + Y α(t)j
Φα (t) = Xα (t)i + Y α(t)j
du champ telle que Φα(0) = αi. On a Φαʹ(0) = V(α,0) = α2j et en particulier, Y ʹα(0) > 0. Donc,
sur un intervalle ] - τ,τ[, la fonction Y α est strictement croissante ; pour 0 < t < τ, on a
Xʹα (t) = Y α (t) > 0 et pour - τ < t < 0,Xʹα(t) < 0.
Ainsi Xα induit un  ∞-difféomorphisme X
∞-difféomorphisme X de ]0,τ[ sur l’intervalle ]α,Xα(τ)[ et un autre
de ]0,τ[ sur l’intervalle ]α,Xα(τ)[ et un autre
 ∞ -difféomorphisme X
∞ -difféomorphisme X de ] - τ,0[ sur l’intervalle ]α,Xα(-τ)[. La fonction
de ] - τ,0[ sur l’intervalle ]α,Xα(-τ)[. La fonction
Y α • X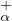 -1 :]α, Xα(τ)[→ R
-1 :]α, Xα(τ)[→ R
se prolonge en une solution positive de (E*) qui n’est autre que φα et la fonction
Y α • X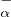 -1 :]α, Xα(-τ)[→ R se prolonge en une solution négative de (E*) qui n’est autre que
ψα .
-1 :]α, Xα(-τ)[→ R se prolonge en une solution négative de (E*) qui n’est autre que
ψα .
Remarquons que cette méthode permet de retrouver, pour α non nul, l’unicité de φα et de
ψα .
L’existence de φ0 et de ψ0 sera vue ultérieurement. Si α ≥ 0 alors φα est dans 
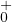 ; on en déduit
que
; on en déduit
que 
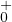 n’est pas vide.
n’est pas vide.
1.4. Convexité
Soit φ une solution de (E*), définie sur ]α,β[. Pour étudier sa convexité on utilise la relation suivante :
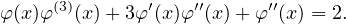 | (3) |
D’après cette relation, si φʹʹ(x) = 0 alors φ(3)(x) = 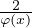 . Si φ est négative (resp. positive) alors
φ(3) (x) < 0 (resp. φ(3)(x) > 0), donc φʹʹ > 0 (resp. φʹʹ < 0) à gauche de x et φʹʹ < 0 (resp.
φʹʹ > 0) à droite de x.
. Si φ est négative (resp. positive) alors
φ(3) (x) < 0 (resp. φ(3)(x) > 0), donc φʹʹ > 0 (resp. φʹʹ < 0) à gauche de x et φʹʹ < 0 (resp.
φʹʹ > 0) à droite de x.
Ainsi tout zéro de φʹʹ est isolé et il ne peut y avoir deux zéros consécutifs donc φʹʹ s’annule au plus une fois. Plus précisément :
Lemme 6.Toute solution positive dont la dérivée seconde s’annule une fois est d’abord strictement concave puis strictement convexe.
Toute solution négative dont la dérivée seconde s’annule une fois est d’abord strictement convexe puis strictement concave.
En particulier, si α < 0 < β, c’est-à-dire si φ = ψα avec α < 0 ou φ est élément de 
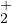 alors 0 est
l’unique zéro de φʹʹ. En effet φʹ(0) = -1 et φʹʹ(0) = 0 d’après derseconde.
alors 0 est
l’unique zéro de φʹʹ. En effet φʹ(0) = -1 et φʹʹ(0) = 0 d’après derseconde.
On déduit du lemme que φʹ est monotone au voisinage de α comme de β et y admet donc des
limites finies ou non. Il est immédiat d’après derpremiere que si α n’est pas nul alors la limite en α
de φʹ est + ∞ si φ est positive et -∞ si φ est négative.
Dans le cas où β = +∞, on montre que φʹ tend vers ±∞ quand x tend vers + ∞. En effet, sinon, par l’absurde, φʹ(x) = m + o(1) en + ∞ pour un certain réel m, puis
φ(x) = mx + o (x), puis x2 = φ(x)(1 + φʹ(x)) = m(1 + m)x + o(x) ;
c’est contradictoire. Ainsi, à l’exception des éléments de 
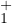 les graphes des solutions de (E*)
admettent une branche parabolique de direction (Oy). De plus,
les graphes des solutions de (E*)
admettent une branche parabolique de direction (Oy). De plus,
x2 ~ φ(x)φʹ(x) puis φ(x)2 ~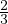 x3 et |φ(x)|~
x3 et |φ(x)|~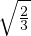 x3⁄2.
x3⁄2.
Supposons maintenant : α = 0 ou β = 0 et étudions la limite en 0 de φʹ. Notons m cette limite.
D’abord m est finie car si m = ±∞, alors φ(x) = o(x2) en 0 et m = 0 : c’est contradictoire. Puis : m(m + 1)x + o (x) = x2 donc m = 0 ou m = -1. Ainsi :
Lemme 7.Soit φ une solution de (E*) telle que 0 est une extrémité de l’intervalle de définition. Alors φ (prolongée) est continûment dérivable en 0 et φʹ(0) vaut 0 ou - 1.
On peut maintenant préciser la convexité des solutions. Dans l’énoncé suivant, on admet
provisoirement l’existence de φ0 et de ψ0. Les fonctions φα et ψα sont prolongées par continuité en
α. Si φα est dans 
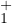 on la prolonge également par continuité en 0 ; là aussi l’existence de
tels α n’est pas encore prouvée. Certains résultats établis ci-dessus sont rappelés dans
l’énoncé.
on la prolonge également par continuité en 0 ; là aussi l’existence de
tels α n’est pas encore prouvée. Certains résultats établis ci-dessus sont rappelés dans
l’énoncé.
- 1.
- Soit α un réel non nul. La fonction ψα est strictement convexe sur [α,w] puis strictement concave sur [w,+∞[ pour un certain w > α. En particulier w = 0 si α < 0. On a ψαʹ(α) = -∞ et lim+∞ψαʹ = -∞.
- 2.
- La fonction ψ0 est strictement concave. Elle est de classe
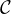 1. On a : ψ0ʹ(0) = -1 et
lim+∞ψ0 ʹ = -∞.
1. On a : ψ0ʹ(0) = -1 et
lim+∞ψ0 ʹ = -∞.
- 3.
- Soit α > 0. La fonction φα est strictement concave sur [α,w] puis strictement convexe sur [w, +∞[ pour un certain w > 0. On a φαʹ(α) = +∞ et lim+∞φαʹ = +∞.
- 4.
- La fonction φ0 est strictement convexe. Elle est de classe
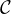 1. On a : φ0ʹ(0) = 0 et
lim+∞φ0 ʹ = +∞.
1. On a : φ0ʹ(0) = 0 et
lim+∞φ0 ʹ = +∞.
- 5.
- Soit α < 0 tel que φα est dans

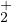 . Alors la fonction φα est strictement concave sur
[α, 0] puis strictement convexe sur [0,+∞[. On a φαʹ(α) = +∞ et lim+∞φαʹ =
+∞.
. Alors la fonction φα est strictement concave sur
[α, 0] puis strictement convexe sur [0,+∞[. On a φαʹ(α) = +∞ et lim+∞φαʹ =
+∞.
- 6.
- Soit α < 0 tel que φα est dans

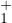 et que φαʹ(0) = -1. Alors φα est strictement
concave. On a φαʹ(α) = +∞.
et que φαʹ(0) = -1. Alors φα est strictement
concave. On a φαʹ(α) = +∞.
- 7.
- Soit α < 0 tel que φα est dans

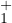 et que φαʹ(0) = 0. Alors φα est strictement concave
sur [α, w] puis strictement convexe sur [w,0] pour un certain w tel que α < w < 0.
On a φα ʹ(α) = +∞.
et que φαʹ(0) = 0. Alors φα est strictement concave
sur [α, w] puis strictement convexe sur [w,0] pour un certain w tel que α < w < 0.
On a φα ʹ(α) = +∞.
Démonstration.
- 1.
- Comme ψα ʹ(α) = -∞ et lim+∞ψαʹ = -∞, la dérivée de ψαʹ s’annule et le lemme s’applique. On a vu que si α < 0, alors w = 0.
- 2.
- D’après derpremiere, ψ0ʹ(x) < -1 pour tout x > 0. D’après le lemme , ψ0 est
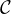 1
donc ψ0 ʹ(0) = -1. Ainsi ψʹ0 est décroissante au voisinage de 0 et d’après le lemme ,
ψʹʹ 0 ne s’annule pas et ψ0 est strictement concave.
1
donc ψ0 ʹ(0) = -1. Ainsi ψʹ0 est décroissante au voisinage de 0 et d’après le lemme ,
ψʹʹ 0 ne s’annule pas et ψ0 est strictement concave.
- 3.
- La preuve est symétrique de celle de 1.
- 4.
- Comme φ0 est dans

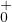 , φʹ0(x) est strictement positif pour x > 0 car φ0 est croissante
au voisinage de 0. Donc d’après le lemme , φ0 est
, φʹ0(x) est strictement positif pour x > 0 car φ0 est croissante
au voisinage de 0. Donc d’après le lemme , φ0 est 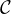 1 et φ0ʹ(0) = 0. Ainsi φʹ0 est
croissante au voisinage de 0 et d’après le lemme , φʹʹ0 ne s’annule pas et φ0 est
strictement convexe.
1 et φ0ʹ(0) = 0. Ainsi φʹ0 est
croissante au voisinage de 0 et d’après le lemme , φʹʹ0 ne s’annule pas et φ0 est
strictement convexe.
- 5.
- On a φα ʹ(0) = -1 puis φαʹʹ(0) = 0 d’après derpremiere et derseconde. Il reste à appliquer le lemme .
- 6.
- On a φα ʹ(x) > -1 pour tout x < 0. Donc φαʹ est strictement décroissante au voisinage de 0. D’après le lemme , φα est strictement concave.
- 7.
- On a φα (x) > 0 pour tout x < 0 et φα(0) = 0. Donc au voisinage de 0, on a φʹα (x) < 0 et comme φʹα(0) = 0, nécessairement φαʹ est strictement croissante au voisinage de 0. De plus φαʹ(α) = +∞ donc φαʹ est strictement décroissante au voisinage de α. Il reste à appliquer le lemme .
2. Solutions de (E) développables en série entière en 0
On procède de la manière usuelle. On considère une série entière formelle S(X) = 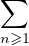 unXn.
Elle est solution dans R[[X]] de l’équation S(X)
unXn.
Elle est solution dans R[[X]] de l’équation S(X)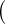 1 + Sʹ(X)
1 + Sʹ(X) = X2 si et seulement
si
= X2 si et seulement
si
u1 (u1 + 1) = 0; u2(u1 + 1) + 2u1u2 = 1,
et pour tout n ≥ 3 :
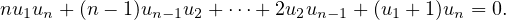 | (4) |
En particulier, u1 vaut 0 ou - 1.
2.1. Le cas u1 = 0
Si u1 = 0 alors u2 = 1. On note désormais (an)n≥0 la suite donnée par
a0 = 0; a1 = 0; a2 = 1
et la relation de récurrence rec1. On a donc pour n ≥ 3
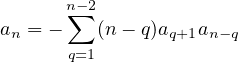 | (5) |
Cette suite jouera un rôle important plus loin.
Montrons que la série entière associée a un rayon de convergence nul. On constate que an est du signe de (-1)n pour tout n ≥ 2. Ainsi, pour tout n ≥ 3, on a :
|an| = 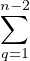 (n - q)|aq+1||an-q|. (n - q)|aq+1||an-q|.
|
Donc pour tout n ≥ 3, on a : |an|≥ (n - 1)|an-1| ; par récurrence immédiate il vient :
|an | ≥ (n - 1)! pour tout n ≥ 2. Il en résulte que la série  anxn a un rayon de convergence nul.
anxn a un rayon de convergence nul.
Il n’existe donc pas de solution φ développable en série entière en 0 telle que φ(0) = 0 et φʹ(0) = 0.
2.2. Le cas u1 = -1
On prouve maintenant :
Théorème 3.L’équation différentielle (E) admet une unique solution f0 développable en série entière en 0, telle que f0(0) = 0. Son intervalle de définition est ]α0,+∞[ pour un certain α0 < 0.
Cette solution vérifie fʹ0(0) = -1. Si g est une solution de (E) définie sur un intervalle I contenant 0 et telle que g(0) = 0 et gʹ(0) = -1 alors I est inclus dans ]α0,+∞[ et g est la restriction de f0 à ]α0,+∞[.
Démonstration.
La relation de récurrence rec1 donne u2 = -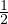 , puis s’écrit, pour n ≥ 3,
, puis s’écrit, pour n ≥ 3,
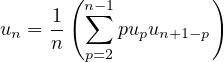 | (6) |
Ces relations définissent une unique suite (un). Montrons que le rayon de convergence de cette série
entière n’est pas nul.
On voit de suite que pour tout n ≥ 2, un est du signe de (-1)n-1. Ainsi, pour tout n ≥ 3, on a :
|un| = 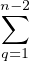 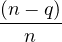 |uq+1||un-q|. |uq+1||un-q|.
|
Considérons la fonction g : x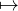
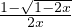 pour x≠0 et g(0) = 1⁄2 ; g est développable en série
entière g(x) =
pour x≠0 et g(0) = 1⁄2 ; g est développable en série
entière g(x) = 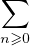 uʹnxn avec un rayon de convergence égal à 1⁄2.
uʹnxn avec un rayon de convergence égal à 1⁄2.
Par ailleurs, g vérifie la relation
xg(x)2 - g(x) +  = 0 = 0
|
pour |x| < 1⁄2. En remplaçant g(x) par son développement, on obtient les relations uʹ0 = 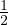 et,
pour tout n ≥ 1,
et,
pour tout n ≥ 1,
uʹn = 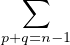 uʹpuʹq. uʹpuʹq.
|
Une récurrence facile donne |up+2|≤ uʹp pour tout p. La série entière  unzn a donc un rayon de
convergence au moins égal à 1⁄2. Sa somme définie sur un intervalle contenant ] - 1⁄2,1⁄2[ est
solution de (E) sur cet intervalle.
__
unzn a donc un rayon de
convergence au moins égal à 1⁄2. Sa somme définie sur un intervalle contenant ] - 1⁄2,1⁄2[ est
solution de (E) sur cet intervalle.
__
2.3. Fin de la démonstration du théorème
Notons S la fonction x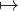
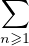 unxn définie sur un certain intervalle ] - R,R[ où R est le rayon de
convergence de cette série entière dont on a vu qu’il était au moins égal à 1⁄2. Elle est solution (non
maximale) de (E) et vérifie S(0) = 0 et Sʹ(0) = -1.
unxn définie sur un certain intervalle ] - R,R[ où R est le rayon de
convergence de cette série entière dont on a vu qu’il était au moins égal à 1⁄2. Elle est solution (non
maximale) de (E) et vérifie S(0) = 0 et Sʹ(0) = -1.
La restriction à [0,R[ de S admet pour prolongement l’élément ψ0 de  - dont on prouve ainsi
l’existence. Son unicité est déjà acquise.
- dont on prouve ainsi
l’existence. Son unicité est déjà acquise.
La restriction à ] - R,0] de S admet pour prolongement un élément φ de 
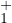 . On note α0 le réel
strictement négatif tel que φ = φα0. La proposition suivante montre que α0 est le seul réel
α tel que φα est dans
. On note α0 le réel
strictement négatif tel que φ = φα0. La proposition suivante montre que α0 est le seul réel
α tel que φα est dans 
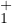 avec φαʹ(0) = -1, ce qui achèvera la preuve du théorème
.
avec φαʹ(0) = -1, ce qui achèvera la preuve du théorème
.
Démonstration.Si α < α0 alors la fonction d = φα -φα0 est définie sur [α0,0] et est strictement
positive sur [α0 , 0[. Supposons par l’absurde que φα ne soit pas dans 
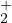 ; elle est alors dans
; elle est alors dans 
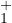 ;
elle tend donc vers 0 en 0. Ainsi d(0) = 0 et dʹ(0)≠0 ; ce n’est possible que si φʹα(0) = -1.
Ainsi,
;
elle tend donc vers 0 en 0. Ainsi d(0) = 0 et dʹ(0)≠0 ; ce n’est possible que si φʹα(0) = -1.
Ainsi,
au voisinage de 0, φα(x) ~-x et φα0(x) ~-x.
Comme 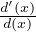 s’écrit -
s’écrit -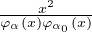 , sa limite en 0 est - 1 ; il en résulte que d(x) tend vers une
limite finie non nulle en 0 et c’est contradictoire.
, sa limite en 0 est - 1 ; il en résulte que d(x) tend vers une
limite finie non nulle en 0 et c’est contradictoire.
Si α0 < α < 0 alors la fonction d = φα0 - φα est définie sur [α,0] et est strictement
positive sur [α, 0[. De plus sa limite en 0 est positive ou nulle donc φα(0) = 0. Ainsi φα
est dans 
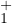 . Supposons par l’absurde que φαʹ(0) ne soit pas nul alors φʹα(0) = -1 et
on prouve comme ci-dessus que d(x) tend vers une limite finie non nulle en 0 et c’est
contradictoire. __
. Supposons par l’absurde que φαʹ(0) ne soit pas nul alors φʹα(0) = -1 et
on prouve comme ci-dessus que d(x) tend vers une limite finie non nulle en 0 et c’est
contradictoire. __
En raccordant φα0 avec ψ0 on obtient la fonction f0 annoncée dans le théorème dont la preuve est
complète. Cette fonction f0 est de plus strictement concave.
La proposition montre en outre que l’ensemble des φ de de 
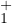 dont la dérivée en 0 est nulle n’est
pas vide et que c’est même l’ensemble évidemment infini des φα où α0 < α < 0. L’ensemble
dont la dérivée en 0 est nulle n’est
pas vide et que c’est même l’ensemble évidemment infini des φα où α0 < α < 0. L’ensemble 
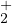 est celui des φα où α < α0.
est celui des φα où α < α0.
3. Les solutions g nulles en 0 et de dérivée nulle en 0
Pour établir l’existence de φ0 on établit la proposition suivante.
Proposition 7.Il existe une solution φ de (E*) définie sur ]0,+∞[ telle que, pour tout x > 0, φ(x) < φα(x) pour tout α < α0 et φ(x) > φα(x) pour tout α de ]0,x[. Cette solution n’est autre que φ0 dont on prouve ainsi l’existence.
Démonstration.
Soit x0 > 0. Considérons l’application Φ1 : α φα(x0) de ] -∞,α0[ dans ]0,+∞[.
φα(x0) de ] -∞,α0[ dans ]0,+∞[.
Soit α < αʹ < α0 ; on a φα > φαʹ sur ]αʹ,+∞[, donc Φ1(α) > Φ1(αʹ). Ainsi Φ1 est strictement décroissante.
Soit α < α0 , et y > Φ1(α). La solution de (E*) qui vaut y en x0 est φαʹ pour un certain
αʹ nécessairement distinct de α. Si on suppose par l’absurde αʹ > α alors φα(αʹ) < 0 car
φα (x) < φαʹ (x) pour tout x ≥ αʹ ; c’est impossible. Donc Φ1 envoie ] -∞,α0[ sur un
sous-intervalle non majoré de ]0,+∞[ ; ce sous-intervalle est ouvert car Φ1 est strictement
décroissante ; c’est donc ]y0,+∞[ pour un certain y0 ≥ 0.
Considérons l’application Φ2 : α φα(x0) de ]0,x0[ dans ]0,+∞[. De façon similaire on
montre que Φ2 envoie ]0,x0[ sur ]0,z0[ pour un certain z0 > 0.
φα(x0) de ]0,x0[ dans ]0,+∞[. De façon similaire on
montre que Φ2 envoie ]0,x0[ sur ]0,z0[ pour un certain z0 > 0.
Soit α < α0 et 0 < αʹ < x0 alors φα(αʹ) > 0 donc Φ1(α) > Φ2(αʹ). Les intervalles
]y0 , +∞[ et ]0, z0 [ sont donc disjoints. Donc z0 ≤ y0.
Soit y un élément quelconque de [z0,y0]. La solution de (E*) dont le graphe passe par (x0,y)
est φα pour un certain α. Puisque φα est définie en x0 on a 0 ≤ α < x0 ou α < α0. De plus,
par construction α n’est ni dans ]0,x0[ ni dans α < α0. Ainsi α = 0 (et y0 = z0).
Réciproquement φ0 vérifie bien pour tout x > 0 les conditions indiquées pour φ. __
L’existence et l’unicité de φ0 sont maintenant établies. Cette fonction est de classe 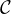 1 et vérifie
φʹ0 (0) = 0. Elle se raccorde en 0 avec φα pour un α quelconque de ]α0,0[ pour constituer une
solution g de (E) qui est
1 et vérifie
φʹ0 (0) = 0. Elle se raccorde en 0 avec φα pour un α quelconque de ]α0,0[ pour constituer une
solution g de (E) qui est 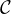 1 et de dérivée nulle en 0, c’est-à-dire un élément de Γ décrit dans le
théorème .
1 et de dérivée nulle en 0, c’est-à-dire un élément de Γ décrit dans le
théorème .

Pour compléter la preuve de ce dernier théorème on va établir :
On fixe un α strictement entre α0 et 0. On note g l’élément de Γ associé. Par hypothèse g est 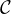 1 en
0 et gʹ(0) = 0. On pose, pour n ≥ 2,
1 en
0 et gʹ(0) = 0. On pose, pour n ≥ 2,
Sn(x) = a2x2 +  + a
nxn, + a
nxn,
|
puis :
| Σn(x) = Sn(x) + μxn |
où μ est un réel non nul. Rappelons que les (an) ont été définis dans la sous-partie .
La preuve du théorème va dépendre des deux propositions suivantes.
Proposition 8.g admet pour tout n ≥ 2 un développement limité à l’ordre n en 0 donné par g(x) = Sn (x) + o(xn).
Démonstration.
D’après les calculs faits en sous-partie pour définir la suite (an), on a :
Sn(x)(Sʹn(x) + 1) - x2 = 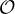 (xn+1). (xn+1).
|
On pose
| Tn(x) = Σn(x)(Σʹn(x) + 1) - x2, |
de sorte que
Σʹn(x) = -1 + 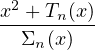 . .
|
On a : Tn (x) = 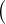 Sn(x)[Sʹn(x) + 1] -x2
Sn(x)[Sʹn(x) + 1] -x2 + μxnSʹn(x) + nμxn-1Sn(x) + μxn + nμ2x2n-1, ce
qui donne :
+ μxnSʹn(x) + nμxn-1Sn(x) + μxn + nμ2x2n-1, ce
qui donne :
| Tn(x) = μxn + o(xn). |
Notons vn la fonction g - Σn. On a : vʹn(x) = gʹ(x) - Σʹn(x), ce qui donne :
vʹn(x) = -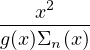 vn(x) - vn(x) -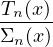 . .
|
La fonction h : x
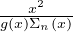 est définie dans un ensemble de la forme Ω =] - k,0[∪]0,k[
avec k > 0. Notons H une primitive de h sur chacun de ces intervalles. La dernière
équation s’écrit
est définie dans un ensemble de la forme Ω =] - k,0[∪]0,k[
avec k > 0. Notons H une primitive de h sur chacun de ces intervalles. La dernière
équation s’écrit 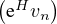 ʹ = -eH
ʹ = -eH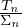 donc, pour s,t de même signe et vérifiant t < s on
a
donc, pour s,t de même signe et vérifiant t < s on
a
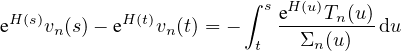 | (7) |
On doit maintenant distinguer deux cas.
a) On se place sur ] - k,0[. On fixe t.
En 0, g(x) et Σn (x) sont équivalents à x2, donc h(x) à 1⁄x2 et H(x) à - 1⁄x. Puis :
Tn (x)⁄Σn (x) est équivalent à μxn-2. Donc l’intégrale figurant dans () diverge vers ±∞ quand s
tend vers 0 à gauche.
⊳ On prend μ = an. Alors μxn-2 > 0 pour x < 0, l’intégrale diverge vers + ∞ donc
lims→0- eH(s) vn (s) = -∞. On dispose donc d’un τ1 > 0 tel que -τ1 < s < 0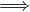 vn(s) < 0,
soit encore g(x) < Sn(x) + anxn pour - τ1 < x < 0.
vn(s) < 0,
soit encore g(x) < Sn(x) + anxn pour - τ1 < x < 0.
⊳ On prend maintenant μ = -an. Alors μxn-2 < 0 pour x < 0. Le même raisonnement fournit un
τ2 > 0 tel que - τ2 < s < 0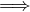 vn(s) > 0 donc g(x) > Sn(x) - anxn = Sn-1(x) pour
- τ2 < x < 0.
vn(s) > 0 donc g(x) > Sn(x) - anxn = Sn-1(x) pour
- τ2 < x < 0.
Finalement, dans un intervalle de la forme ] - τ,0[, τ > 0 on a
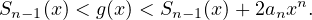
g(x) = Sn-1 (x) + o(xn-1).
b) On se place sur ]0,k[ et on fixe s.
Cette fois, lim t→0+eH(t) = 0 et on a toujours Tn(x)⁄Σn(x) ~ μxn-2. Dès lors, (eHvn)ʹ est du
signe de - μ dans un intervalle de la forme ]0,τʹ1[. D’autre part, la fonction eHvn, prolongée par
continuité, s’annule en 0.
⊳ On prend μ = 1. eHvn décroît dans ]0,τʹ1[ donc vn(x) < 0 pour x dans cet intervalle ce qui
donne g(x) < Sn (x) + xn.
⊳ On prend ensuite μ = -1. eHvn croît dans ]0,τʹ1[ donc vn(x) > 0 dans cet intervalle ce qui
donne g(x) > Sn (x) - xn.
Finalement, dans un intervalle de la forme ]0,τʹ[ on a
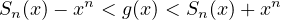
g(x) = Sn-1 (x) + o(xn-1).
Comme n est arbitraire, le résultat est établi. __
Proposition 9.Pour tout entier p ≥ 0, pour tout entier n ≥ 0 la dérivée p-ième de g admet
un développement limité à l’ordre n donné par g(p)(x) = S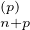 (x) + o(xn).
(x) + o(xn).
Démonstration.La démonstration se fait par récurrence sur p, le résultat étant établi pour p = 0.
On suppose le résultat établi pour tous les entiers inférieurs ou égaux à p. On suppose donc
que, pour tout n, on a g(k)(x) = S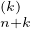 (x) + o(xn) pour 0 ≤ k ≤ p. On dérive p fois la
relation g(x)gʹ(x) + g(x) - x2 = 0. On pose A(x) = x2. Il vient :
(x) + o(xn) pour 0 ≤ k ≤ p. On dérive p fois la
relation g(x)gʹ(x) + g(x) - x2 = 0. On pose A(x) = x2. Il vient :
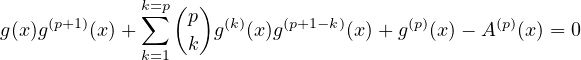
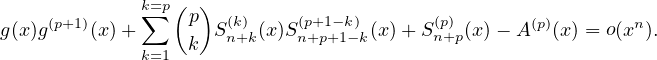 | (8) |
La série formelle S(X) = 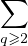 aqXq vérifie S(X)Sʹ(X) + S(X) - X2 = 0. On en
déduit
aqXq vérifie S(X)Sʹ(X) + S(X) - X2 = 0. On en
déduit
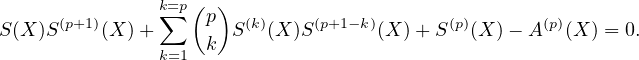
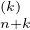 (X) mod Xn+1 donc
(X) mod Xn+1 donc
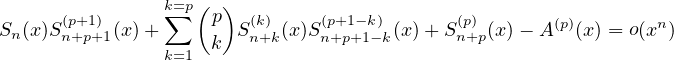 | (9) |
donc, en retranchant () de () :
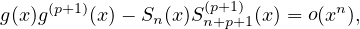
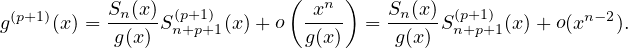
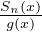 = 1 + o (xn-2) et S
= 1 + o (xn-2) et S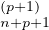 (x) = S
(x) = S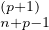 (x) + o(xn-2). On a donc le développement
limité attendu de g(p+1) à l’ordre n - 2. L’entier n étant quelconque, ceci achève la
récurrence. __
(x) + o(xn-2). On a donc le développement
limité attendu de g(p+1) à l’ordre n - 2. L’entier n étant quelconque, ceci achève la
récurrence. __
Le théorème en résulte puisque pour tout p de N, limx→0g(p)(x) = S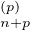 (0) = p!ap.
(0) = p!ap.
On reprend les notations de la sous-partie . Puisque S admet f0 pour prolongement, on a R ≤|α0|. Une étude numérique montre : α0 ≈-0.86 ; d’autres études numériques (règle de d’Alembert, règle de Cauchy) aboutissent à des valeurs voisines de - 0.86.
On montre à présent :
| R = -α0. |
On utilise pour cela le prolongement analytique de S dans le plan complexe. Le premier
théorème assure l’analyticité des solutions de (E*) prolongées dans l’ouvert C × C*.
Théorème 5.Soit F : Ω →C une fonction analytique de deux variables où Ω est un ouvert de C 2 . Soit (a, b) un élément de Ω.
1) Il existe un couple (U,Φ) où U est un ouvert de C contenant a et Φ : U → C est
une fonction analytique vérifiant Φ(a) = b et, pour tout z de U, (z,Φ(z)) est dans Ω et
Φʹ(z) = F(z, Φ(z)). Deux solutions (U1,Φ1) et (U2,Φ2) de ce problème sont telles que Φ1
et Φ2 coïncident sur U1 ∩ U2.
2) Si le développement en série entière de deux variables de F autour de (a,b) est à coefficients réels alors le développement en série entière de Φ selon les puissances de z - a est à coefficients réels.
On en trouvera par exemple la preuve dans le livre de H. Cartan, Théorie élémentaire des fonctions
analytiques d’une ou plusieurs variables complexes, p. 214 et suivantes.
La fonction F : (X,Y )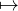 - 1 +
- 1 + 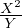 est manifestement analytique dans Ω. D’après le
théorème , toutes les solutions de l’équation (E
est manifestement analytique dans Ω. D’après le
théorème , toutes les solutions de l’équation (E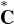 ) : Y ʹ = -1 +
) : Y ʹ = -1 + 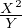 sont analytiques.
sont analytiques.
On revient maintenant à la fonction S ; on note encore S la fonction z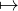
 n≥1unzn, définie dans
le disque ouvert {z
n≥1unzn, définie dans
le disque ouvert {z  C||z| < R}.
C||z| < R}.
Raisonnons par l’absurde et supposons R < |α0|. Pour tout x de ] -R,0[ on a S(x) = f0(x) donc S admet en - R une limite finie b = f0(-R) et cette limite n’est pas nulle.
Posons S1 (z) =  n≥2|un|zn. Le rayon de convergence de cette série entière est R. On applique
un autre résultat adapté à ce type de fonction.
n≥2|un|zn. Le rayon de convergence de cette série entière est R. On applique
un autre résultat adapté à ce type de fonction.
Théorème 6.Soit (an) une suite de réels positifs telle que la série entière Σanzn a un rayon
de convergence R > 0. Alors R est un point singulier pour la fonction T : z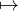
 n≥0anzn
c’est-à-dire que T n’admet aucun prolongement analytique défini autour de R.
n≥0anzn
c’est-à-dire que T n’admet aucun prolongement analytique défini autour de R.
Un énoncé équivalent figure en exercice dans le livre de Walter Rudin, Analyse réelle et complexe,
p. 380.
La fonction S1 n’admet donc pas de prolongement analytique autour de R. Mais comme S(x) = -x - S1 (-x) la fonction S n’admet pas de prolongement analytique autour de - R.
Appliquons le théorème au point (a,b) = (-R,f0(R)). On dispose donc d’un voisinage U de -R
dans C et d’une fonction analytique Φ : U → C solution de (E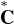 ) dans U. On peut supposer que U
est un disque. La restriction à U ∩ R de Φ vérifie
) dans U. On peut supposer que U
est un disque. La restriction à U ∩ R de Φ vérifie
Φ(a) = b et Φʹ(x) = -1 + 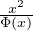
et est à valeurs réelles d’après le point 2) du théorème . Ainsi Φ(x) = S(x) sur un certain intervalle ] - R, -R + h[ avec h > 0. Les fonctions Φ et S sont analytiques donc Φ(z) = S(z) pour tout z de l’ouvert convexe U ∩ D.
Ceci contredit que - R soit un point singulier pour S. Donc R = -α0.
Dans sa réponse partielle Jérôme Demange prouve l’existence et l’unicité d’une solution g de (E)
définie sur ] - 1⁄2,+∞[ et telle que g(0) = 0 et gʹ(0) = -1 en la construisant par itération. Il
prouve ensuite qu’elle est 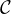 ∞ et qu’elle développable en série entière sur ] - 1⁄4,1⁄4[ par une
méthode semblable à celle de la réponse ci-dessus.
∞ et qu’elle développable en série entière sur ] - 1⁄4,1⁄4[ par une
méthode semblable à celle de la réponse ci-dessus.
Dans sa réponse partielle Omar Sonebi montre que si g est solution de (E) telle que g(0) = 0 alors
elle n’est pas développable en série entière si gʹ(0) = 0. Dans le cas où gʹ(0) = -1, il montre que g
est développable en série entière par une méthode très différente de celle que nous avons vue et
dont voici un résumé.
Reprenons la suite (un) de la sous-partie . On a :
u0 = 0; u1 = -1 ; u2 = -1⁄2 ; pour n ≥ 3, un = 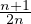
 2≤i≤n-1uiun+1-i.
2≤i≤n-1uiun+1-i.
On cherche par récurrence une majoration |un|≤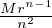 pour tout n ≥ 2. Il faut donc Mr ≥ 2 et la
preuve par récurrence fonctionne si
pour tout n ≥ 2. Il faut donc Mr ≥ 2 et la
preuve par récurrence fonctionne si
MAn ≤ 1 pour tout n ≥ 3, où An = 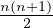
 2≤i≤n-1
2≤i≤n-1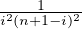 .
.
On montre que la suite (An) est majorée. Notons α un majorant. Prenons M = 1⁄α, puis
r = 2⁄M = 2α. On montre ainsi que, puisque les séries Σunxn et Σn2unrn ont même rayon de
convergence R, ce dernier est minoré par 1⁄(2α).
Une étude détaillée montre que la méthode d’Omar Sonebi conduit à une minoration :
| R ≥ 0.66094 |
Après décomposition en éléments simples de la fraction 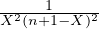 on obtient l’expression
exacte :
on obtient l’expression
exacte :
An = 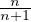
 2≤i≤n-1
2≤i≤n-1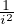 +
+ 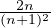
 2≤i≤n-1
2≤i≤n-1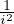 .
.
La limite de An est donc A = ζ(2) - 1. Mais A n’est pas le sup de (An). En effet An = A + ρn où
ρn = 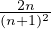
 2≤i≤n-1
2≤i≤n-1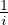 -
-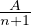 -
-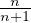
 i≥n
i≥n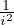
et ρn ~ 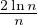 . Donc An > A pour n assez grand. On majore :
. Donc An > A pour n assez grand. On majore :
ρn ≤ ρʹn = 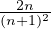
 2≤i≤n-1
2≤i≤n-1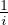 -
-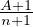 car
car  i≥
i≥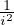 ≥
≥ .
.
L’étude numérique montre que la suite (ρʹn) atteint son maximum pour n = 7, la valeur
de ce maximum étant 0.11157… ; on a A = 0.64493…, donc on prend α = 1.7565 et
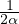 = 0.66094.
= 0.66094.
[Questions-Reponses]