[Table des matières]
Agrégation Interne de Mathématiques
Deuxième Épreuve 2020
7047Différentiabilité de la distance à une partie
Corrigé par Bernard Randé, comité de rédaction de la RMS
Résumé
Le problème porte sur la distance à une partie fermée non vide F d’un espace euclidien. L’hypothèse que la dimension est finie permet de s’appuyer sur la compacité. La différentiabilité de la fonction distance à F est l’un des thèmes principaux. Le résultat le plus intéressant est une condition nécessaire et suffisante de différentiabilité de cette fonction en un point du complémentaire de F ; il fait l’objet de deux des dernières parties. Notons que, puisqu’on caractérise en termes de différentiabilité les parties F telles que, pour tout x dans E, il existe un unique y de F réalisant la distance de x à F, un théorème de Motzkin bien connu entraîne que cette caractérisation est celles des convexes de E.
L’épreuve a dû bien sélectionner les candidats, car elle est progressive. Elle est néanmoins trop longue. La partie VI oppose en outre quelques difficultés.
Le problème est élémentaire, assez approprié aux candidats à l’agrégation interne et manifestement
rédigé par des gens légèrement pressés. Par exemple, pour montrer que la norme euclidienne n’est
pas différentiable en 0, il aurait suffit de montrer que sa restriction à une droite vectorielle n’est pas
dérivable. Il y a quelques petites erreurs (il faut supposer n ≥ 2 dans la question 18, d’ailleurs
guidée par un chien d’aveugle lui-même aveugle) ou incongruités. Si l’on voulait à tout prix faire
montrer au candidat que la série 
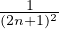 converge, il aurait été préférable de le lui demander
lors d’une question préliminaire, avant de lui faire utiliser l’égalité de Parseval, qui contient cette
convergence. Les questions 12 et 13 sont au moins ambiguës, puisque le statut des bornes n’est pas
précisé.
converge, il aurait été préférable de le lui demander
lors d’une question préliminaire, avant de lui faire utiliser l’égalité de Parseval, qui contient cette
convergence. Les questions 12 et 13 sont au moins ambiguës, puisque le statut des bornes n’est pas
précisé.
Partie I : résultats préliminaires
1. ∙ Si x  F, comme ∥x - x∥ = 0, on a d(x,F) = 0.
F, comme ∥x - x∥ = 0, on a d(x,F) = 0.
∙ Si d(x, F) = 0, par définition de l’infimum, il existe une suite (fn)n≥0  FN telle que
∥x - fn ∥ → d(x,F) = 0. Donc fn → x et, comme F est fermé, x
FN telle que
∥x - fn ∥ → d(x,F) = 0. Donc fn → x et, comme F est fermé, x  F .
F .
2. a) On a d(y, F) ≤∥y - f∥≤∥y - x∥ + ∥x - f∥.
b) Par passage à l’infimum sur f  F , on obtient que d(y,F) ≤∥y - x∥ + d(x,F) et donc
que
F , on obtient que d(y,F) ≤∥y - x∥ + d(x,F) et donc
que
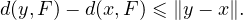
Par symétrie, d(x,F) - d(y,F) ≤∥y - x∥ et finalement  d(y,F) - d(x,F)
d(y,F) - d(x,F) ≤∥y - x∥.
≤∥y - x∥.
3. a) L’ensemble K, qui contient x0, est fermé, comme intersection de fermés, et borné, car inclus dans une boule. Comme E est de dimension finie, il est compact.
b) La fonction x d(x,F) est continue, car lipschitzienne, et réalise donc son minimum sur le
compact K, en un point y. On a donc, pour tout f
d(x,F) est continue, car lipschitzienne, et réalise donc son minimum sur le
compact K, en un point y. On a donc, pour tout f  K, ∥x - y∥≤∥x - f∥. En particulier,
∥x - y∥ ≤ ∥x - x0∥. Si f
K, ∥x - y∥≤∥x - f∥. En particulier,
∥x - y∥ ≤ ∥x - x0∥. Si f  F et f ⁄
F et f ⁄ K, on a ∥x-f∥ > ∥x-x0∥≥∥x-y∥. Finalement, pour
tout f
K, on a ∥x-f∥ > ∥x-x0∥≥∥x-y∥. Finalement, pour
tout f  F, ∥x - y∥≤∥x - f∥, et donc y
F, ∥x - y∥≤∥x - f∥, et donc y  Γ(x).
Γ(x).
4. a) On a
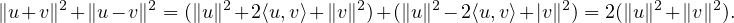
b) Posons d := d(x,F). On a donc ∥f - x∥ = ∥fʹ- x∥ = d. Par application de la question a,
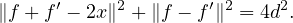
Donc
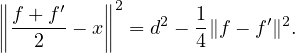
Donc 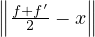 < d.
< d.
Nous avons vu que Γ(x) n’est pas vide. De plus, si f et fʹ sont dans Γ(x), 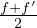
 F par
convexité de F. Ce qui précède montre que f ne peut être différent de fʹ. Donc Γ(x) est un
singleton.
F par
convexité de F. Ce qui précède montre que f ne peut être différent de fʹ. Donc Γ(x) est un
singleton.
c) ∙ On peut écrire, en posant a := f - π(x) et b := π(x) - x,
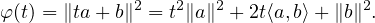
∙ Pour t  [0, 1], puisque (1 - t)π(x) + tf
[0, 1], puisque (1 - t)π(x) + tf  F , on a φ(t) ≥ d2 = φ(0). Donc φ réalise en 0 son
minimum sur [0, 1], ce qui entraîne que φʹ(0) ≥ 0, soit 2⟨a,b⟩≥ 0, ou encore
F , on a φ(t) ≥ d2 = φ(0). Donc φ réalise en 0 son
minimum sur [0, 1], ce qui entraîne que φʹ(0) ≥ 0, soit 2⟨a,b⟩≥ 0, ou encore
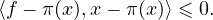
d) On a en particulier
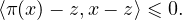
D’autre part, d’après c,
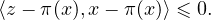
Par somme,
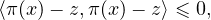
Partie II : étude en dimension 1
5. On a bien entendu d{0}(x) = |x|. Donc d{0} est non dérivable en 0, et dérivable sur R*, de
dérivée en x égale à  = sgn x.
= sgn x.
6. Le complémentaire de Z est la réunion des ]n,n + 1[, lorsque n décrit Z, donc est ouvert dans R. Ainsi, Z est fermé dans R.
7. On a dZ (x + 1) = min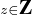 |x + 1 - z| = min
|x + 1 - z| = min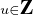 |x - u| = dZ(x), grâce à la réindexation
u = z - 1. De plus,
|x - u| = dZ(x), grâce à la réindexation
u = z - 1. De plus,
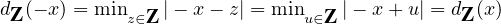
8. Si x 
![[]
0,12](/numeros/RMS130-4/RMS130-4556x.png) , x ≤|x - n| pour n
, x ≤|x - n| pour n  Z. En effet, si n ≥ 1, |x - n| = n - x et on a bien
2x ≤ 1 ≤ n, et si n ≤ 0, on a bien x ≤ x - n. Donc dZ(x) = |x - 0| = x.
Z. En effet, si n ≥ 1, |x - n| = n - x et on a bien
2x ≤ 1 ≤ n, et si n ≤ 0, on a bien x ≤ x - n. Donc dZ(x) = |x - 0| = x.
Si x 
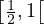 , alors 1 - x
, alors 1 - x  ]0,
]0,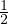 ] et donc, par parité et 1-périodicité,
] et donc, par parité et 1-périodicité,
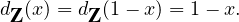
![]()
9. La fonction dZ est manifestement dérivable en tout point de ![]0, 1[
2](/numeros/RMS130-4/RMS130-4560x.png) ∪
∪![]1,1[
2](/numeros/RMS130-4/RMS130-4561x.png) . Elle n’est pas
dérivable en
. Elle n’est pas
dérivable en 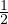 , puisque ses dérivées à gauche et à droite sont différentes. Elle n’est pas dérivable en
0, puisque sa dérivée à droite vaut 1 et donc, par parité, sa dérivée à gauche est égale à
- 1.
, puisque ses dérivées à gauche et à droite sont différentes. Elle n’est pas dérivable en
0, puisque sa dérivée à droite vaut 1 et donc, par parité, sa dérivée à gauche est égale à
- 1.
10. a) Puisque dZ (notée ici f) est paire, bn(f) = 0 et, pour n ⁄= 0,
![∫ 12 4 1 4 ∫ 12
an(f)= 4 tcos2πnt dt = 2πn[tsin 2πnt]20 - 2πn sin 2πnt dt
04 1 1 0
= -----2[cos2πnt]20 = -2-2(cosπn - 1).
(2πn) π n](/numeros/RMS130-4/RMS130-4563x.png)
Donc an (f) = 0 si n est pair et a2p+1(f) = -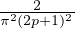 .
.
Enfin, a0 (f) = 2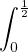 t d t = [t2]
t d t = [t2]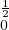 =
= 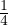 .
.
b) Comme f est de classe 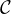 1 par morceaux et continue, elle est somme de sa série de Fourier, la
convergence de cette dernière étant normale, donc uniforme et simple.
1 par morceaux et continue, elle est somme de sa série de Fourier, la
convergence de cette dernière étant normale, donc uniforme et simple.
c) ∙ On a, pour tout x dans R,
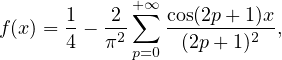
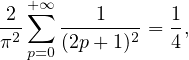

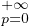
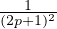 =
= 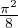 . De plus, puisque la série
. De plus, puisque la série 
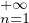
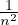 est positive convergente, en notant S sa
somme,
est positive convergente, en notant S sa
somme,
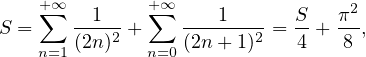
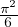 .
.
∙ D’après l’égalité de Parseval,
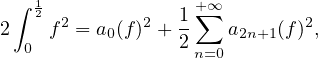
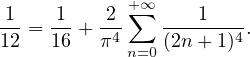
Donc
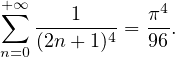
De plus, puisque la série 
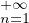
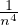 est positive convergente, en notant T sa somme,
est positive convergente, en notant T sa somme,
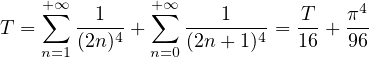
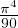 . Enfin,
. Enfin, 
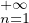
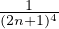 =
= 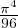 - 1.
- 1.
11. a) La relation ~ est évidemment symétrique. Elle est réflexive puisque, si x  Ω, il existe
]a, b[ contenant x et inclus dans Ω, par définition d’un ouvert. Supposons à présent que
x ~ y et y ~ z. Soit ]a,b[⊂ Ω contenant x et y, ]c,d[⊂ Ω contenant y et z. En particulier,
]a, b[∩]c, d[ est non vide, comme contenant y, et donc ]a,b[∪]c,d[ est un intervalle, ouvert
comme réunion de deux ouverts. Il contient x et z et est inclus dans Ω. Donc ~ est
transitive.
Ω, il existe
]a, b[ contenant x et inclus dans Ω, par définition d’un ouvert. Supposons à présent que
x ~ y et y ~ z. Soit ]a,b[⊂ Ω contenant x et y, ]c,d[⊂ Ω contenant y et z. En particulier,
]a, b[∩]c, d[ est non vide, comme contenant y, et donc ]a,b[∪]c,d[ est un intervalle, ouvert
comme réunion de deux ouverts. Il contient x et z et est inclus dans Ω. Donc ~ est
transitive.
b) Nous savons que les classes d’équivalence forment une partition de Ω. Montrons que la classe de
x est un intervalle ouvert. Pour tout y dans cette classe, il existe ]a(y),b(y)[ inclus dans Ω et
contenant x et y. Donc cl(x) ⊂∪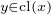 ]a(y),b(y)[. D’un autre côté, si z
]a(y),b(y)[. D’un autre côté, si z  ]a(y),b(y)[, z ~ x,
donc z
]a(y),b(y)[, z ~ x,
donc z  cl (x). Donc cl(x) = ∪
cl (x). Donc cl(x) = ∪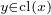 ]a(y),b(y)[. Comme réunion d’intervalles ouverts contenant
tous x, cl (x) est un intervalle ouvert. Notons que cet intervalle est de la forme ]a,b[ avec
- ∞ ≤ a < b ≤ +∞.
]a(y),b(y)[. Comme réunion d’intervalles ouverts contenant
tous x, cl (x) est un intervalle ouvert. Notons que cet intervalle est de la forme ]a,b[ avec
- ∞ ≤ a < b ≤ +∞.
c) À chaque classe d’équivalence C, associons un rationnel qC y appartenant. Puisque deux classes
distinctes sont disjointes, C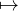 qC est injective. Comme Q est dénombrable, l’ensemble des classes
est dénombrable (au sens large). En notant i =
qC est injective. Comme Q est dénombrable, l’ensemble des classes
est dénombrable (au sens large). En notant i = ![]ai,bi[](/numeros/RMS130-4/RMS130-4594x.png) pour tout i
pour tout i  I, on obtient alors le résultat
voulu.
I, on obtient alors le résultat
voulu.
12. a) Remarquons que, si ai0  R, ai0
R, ai0  F , faute de quoi il serait dans Ω, ouvert, et il existerait
ϵ > 0 tel que ]ai0 -ϵ,ai0 + ϵ[⊂ Ω. Par conséquent, cet intervalle rencontrerait cl(x), en un point y,
et tous les éléments de ]ai0 - ϵ,ai0 + ϵ[ seraient dans cl(y) = cl(x). En particulier,
ai0
F , faute de quoi il serait dans Ω, ouvert, et il existerait
ϵ > 0 tel que ]ai0 -ϵ,ai0 + ϵ[⊂ Ω. Par conséquent, cet intervalle rencontrerait cl(x), en un point y,
et tous les éléments de ]ai0 - ϵ,ai0 + ϵ[ seraient dans cl(y) = cl(x). En particulier,
ai0  cl (x) =]ai0 ,bi0[, ce qui est une contradiction. De même, bi0
cl (x) =]ai0 ,bi0[, ce qui est une contradiction. De même, bi0  F lorsque bi0 est
réel
F lorsque bi0 est
réel
Il en résulte manifestement, comme dans la question 8, que
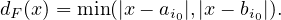
b) Puisque ]ai0 , bi0[ est ouvert, la dérivabilité de dF en x équivaut à la dérivabilité en x de la
restriction de dF à ]ai0,bi0[. Par conséquent, dF est dérivable en x si et seulement si x ⁄= 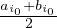 lorsque les deux bornes sont réelles. Dans le cas contraire, dF est dérivable en tout point de
]ai0 , bi0 [.
lorsque les deux bornes sont réelles. Dans le cas contraire, dF est dérivable en tout point de
]ai0 , bi0 [.
13. Comme dF est nulle sur un voisinage de x, elle est dérivable en x, de dérivée nulle.
14. a) De ce que l’adhérence du complémentaire de F est égale à ] -∞,0] ∪ [1,+∞[, on déduit que Fr (F) = {0,1}. La fonction dF est nulle sur [0,1], donc sa dérivée à droite en 0 est nulle. Sur ] -∞,0], dF(x) = -x, donc la dérivée à gauche en 0 est égale à - 1. Donc dF n’est pas dérivable en 0. De même, elle n’est pas dérivable en 1.
b) (i) Comme Ω est ouvert, F est fermé. De plus, 0 <  -
-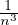 <
<  ≤
≤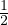 , donc Ω ⊂]0,
, donc Ω ⊂]0,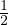 [. En
particulier, 0
[. En
particulier, 0  F. Mais
F. Mais  -
-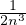 → 0, donc 0 est adhérent à Ω. Ainsi, 0
→ 0, donc 0 est adhérent à Ω. Ainsi, 0  Fr(F).
Fr(F).
(ii) Il s’agit de montrer que les intervalles définissant Ω sont disjoints, c’est-à-dire l’inégalité
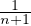 ≤
≤ 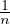 -
-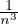 . Cette inégalité équivaut à
. Cette inégalité équivaut à
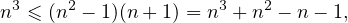
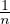 -
- 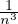 < x <
< x < 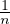 , et ce qu’on vient de montrer assure alors que
, et ce qu’on vient de montrer assure alors que 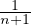 < x <
< x < 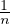 , donc
n <
, donc
n <  < n + 1, ce qui entraîne n =
< n + 1, ce qui entraîne n = 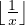 .
.
(iii) Si x  F, l’inégalité est évidente pour toute valeur de C. Dans le cas contraire, x appartient à
un unique intervalle
F, l’inégalité est évidente pour toute valeur de C. Dans le cas contraire, x appartient à
un unique intervalle ![] 1 1 1[
n - n3,n](/numeros/RMS130-4/RMS130-4615x.png) . Or
. Or 
 F , donc
F , donc
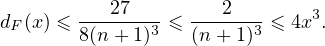
∙ Puisque dF (x) =x→0+o(x), dF est dérivable à droite en 0, de dérivée à droite nulle. Comme, par ailleurs, dF est nulle sur ] -∞,0], dF est dérivable en 0
Partie III : étude de cas particuliers en dimension n
15. a) On a évidemment dF(x) = ∥x - x0∥, et Γ(x) = {x0}.
b) On considère une base orthonormée (ei)1≤i≤n de E et l’on note, lorsque x  E, xi := ⟨x,ei⟩.
Puisque g(x) =
E, xi := ⟨x,ei⟩.
Puisque g(x) = 
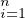 (xi - x0i)2, g est polynomiale, donc de classe
(xi - x0i)2, g est polynomiale, donc de classe 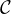 ∞. De plus,
∞. De plus,
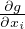 (x) = 2(xi - x0i). Donc (∇g)(x) = 2(x - x0).
(x) = 2(xi - x0i). Donc (∇g)(x) = 2(x - x0).
c) Puisque x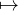
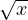 est de classe
est de classe 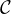 ∞
sur ]0,+∞[, dF est, par composition, de classe
∞
sur ]0,+∞[, dF est, par composition, de classe 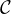 ∞ sur
l’ouvert E - {x0 }. De plus, g(x) = (dF(x))2, donc
∞ sur
l’ouvert E - {x0 }. De plus, g(x) = (dF(x))2, donc
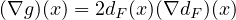
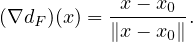
d) ∙ Par définition de la différentiabilité,
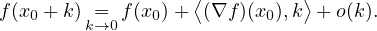
Donc
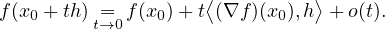
∙ On obtient ainsi
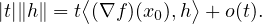
Divisant par t > 0, puis par t < 0, et faisant tendre t vers 0, on obtient que ∥h∥ = 0, ce qui est une contradiction en considérant un vecteur h non nul.
16. a) On sait que la distance de x à F est réalisée pour l’unique vecteur y de F tel que
x - y  F⊥ , et que ce vecteur y est le projeté orthogonal de x sur F .
F⊥ , et que ce vecteur y est le projeté orthogonal de x sur F .
b) Soit (ei )1≤i≤p une base orthonormée de F , complétée en une base orthonormée (ei)1≤i≤n de E. Alors
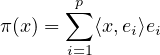
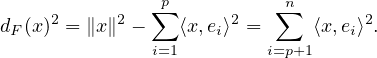
Comme application polynomiale, d est de classe
est de classe  ∞ et (dans la base (ei)),
∞ et (dans la base (ei)),
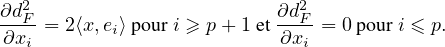
Par conséquent, (∇d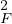 )(a) = 2(a - π(a)).
)(a) = 2(a - π(a)).
c) Comme ci-dessus, dF est de classe 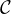 ∞ sur E - F , et
∞ sur E - F , et
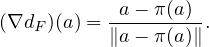
d) ∙ Soit h  F⊥ . On utilise à nouveau
F⊥ . On utilise à nouveau
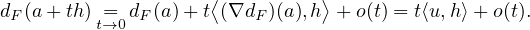
Comme dF (a + th) = ∥a + th - π(a + th)∥ = ∥th∥, on obtient que
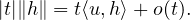
Divisant par t > 0 et faisant tendre t vers 0, on obtient que ∥h∥ = ⟨u,h⟩.
∙ En appliquant ce qui précède à - h, on obtient que h = 0, ce qui est une contradiction, puisque l’on peut choisir h ⁄= 0 dans F⊥.
17.
a)
![]()
b) Puisque (x, y) -y et (x,y)
-y et (x,y) y -x2 sont polynomiales, donc continues, l’image réciproque
de [0, +∞[ par chacune de ces fonctions est un fermé de R2. Donc F , réunion de deux fermés, est
un fermé de R 2 .
y -x2 sont polynomiales, donc continues, l’image réciproque
de [0, +∞[ par chacune de ces fonctions est un fermé de R2. Donc F , réunion de deux fermés, est
un fermé de R 2 .
c) Bien sûr, (0, 0)  F . De plus, (
F . De plus, (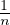 ,
,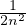 ) n’est pas dans F pour n ≥ 1. Donc (0,0) est adhérent au
complémentaire de F , et finalement appartient à la frontière de F .
) n’est pas dans F pour n ≥ 1. Donc (0,0) est adhérent au
complémentaire de F , et finalement appartient à la frontière de F .
d) Si u  F, l’inégalité est évidente. Supposons que u = (x,y) ne soit pas dans F . On a donc
0 < y < x2 . Par suite, dF(u) ≤∥u - (x,x2)∥ = |y - x2|≤ x2 ≤∥u∥2.
F, l’inégalité est évidente. Supposons que u = (x,y) ne soit pas dans F . On a donc
0 < y < x2 . Par suite, dF(u) ≤∥u - (x,x2)∥ = |y - x2|≤ x2 ≤∥u∥2.
e) On vient de voir que dF(u) = O(∥u∥2) = dF(0) + o(u), donc que d F est différentiable en 0, de gradient nul.
Partie IV : distance à la sphère unité
18. On supposera ici n ≥ 2.
a) On a l’encadrement 1 ≤ dimvect(a,u,y) ≤ 2. Si la dimension de vect(a,u,y) vaut 2, P := vect (a, u, y) répond à la question. Sinon, on considère un vecteur z non dans vect(a,u,y) et on pose P := vect(a,u,y,z).
b) Puisque F ∩ P est l’ensemble des vecteurs de norme 1 de P , c’en est le cercle unité.
c) Si y  F, on a, compte tenu de l’égalité ∥a - u∥ =
F, on a, compte tenu de l’égalité ∥a - u∥ =  1 -∥a∥
1 -∥a∥ ,
,
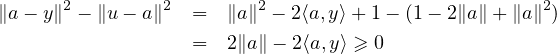
19. En particulier, pour tout a dans E \{0},
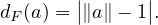
20. Si ∥a∥ > 1, dF(x) = ∥x∥- 1 au voisinage de a, donc dF est différentiable en a. De plus,
(∇dF )(a) = 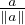 . Si 0 < ∥a∥ < 1, dF(x) = 1 -∥x∥ au voisinage de a, donc dF est différentiable
en a, et (∇dF )(a) = -
. Si 0 < ∥a∥ < 1, dF(x) = 1 -∥x∥ au voisinage de a, donc dF est différentiable
en a, et (∇dF )(a) = -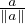 .
.
21. Puisque 1 = d(0,F), l’ensemble des y de F tels que ∥y - 0∥ = d(0,F) est égal F.
22. Soit x  R
R 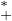 a, que l’on écrit x = ta. On a dF(x) = |t - 1|. Par conséquent, dF n’est
pas dérivable en a selon le vecteur a. Ceci entraîne que dF n’est pas différentiable en
a.
a, que l’on écrit x = ta. On a dF(x) = |t - 1|. Par conséquent, dF n’est
pas dérivable en a selon le vecteur a. Ceci entraîne que dF n’est pas différentiable en
a.
23. a) On a dF (tv) =  |t
|t - 1| = 1 -|t|. Cette fonction n’est pas dérivable en 0.
- 1| = 1 -|t|. Cette fonction n’est pas dérivable en 0.
b) Par conséquent, dF n’est pas différentiable en 0.
Partie V : une condition nécessaire de différentiabilité à l’extérieur de F
24. a) L’inégalité demandée résulte du caractère 1-lipschitzien de dF.
b) Puisque
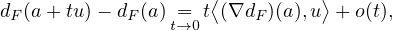
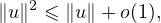
25. a) Puisque x  [y,a], on peut écrire x = (1 - t)y + ta avec t
[y,a], on peut écrire x = (1 - t)y + ta avec t  [0,1] et donc
[0,1] et donc
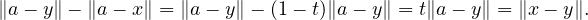
b) On a bien entendu dF(x) ≤∥x - y∥. Comme dF est 1-lipschitzienne,
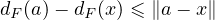
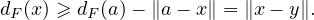
Finalement, dF (x) = ∥x - y∥.
26. a) Le vecteur a - tv appartient à [a,a - (a - y)] = [a,y] et, d’après la question 25,
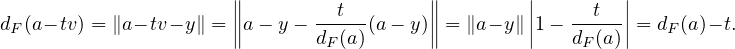
b) On utilise la différentiabilité de dF :
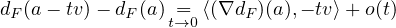
Comme ∥u∥ ≤ 1 et ∥v∥ = 1, l’inégalité de Cauchy & Schwarz montre que ∥u∥ = 1 et que u = v.
c) Comme u = v, on a
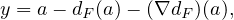
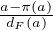 .
.
Partie VI : étude de la réciproque
27. a) La suite (xp - a)p≥0 est convergente, donc bornée. Soit b  F . On a
F . On a
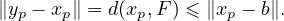
Comme (xp - b) et (xp) sont bornées, (yp) est bornée.
b) Comme suite bornée d’un espace vectoriel normé de dimension finie, (yp) admet une valeur d’adhérence.
c) Comme F et E - V sont fermés, l  F ∩ (E - V ).
F ∩ (E - V ).
d) On a xφ(p) - yφ(p) → a - l, donc d(xφ(p),F) →∥a - l∥. Comme d(⋅,F) est continue,
d(a, F) = ∥a - l∥ et, comme l  F , l = π(a). Or π(a)
F , l = π(a). Or π(a)  V , alors que l ⁄
V , alors que l ⁄ V : c’est la contradiction
cherchée.
V : c’est la contradiction
cherchée.
28. a) Puisque a ⁄ F , a ⁄= π(a) et donc R > 0. En outre, B(a,R) ∩ F ne contient que π(a),
d’après l’hypothèse sur Γ(a).
F , a ⁄= π(a) et donc R > 0. En outre, B(a,R) ∩ F ne contient que π(a),
d’après l’hypothèse sur Γ(a).
b, c) ∙ Notons que y - x ⁄= 0. On a
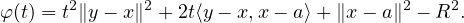
Donc φ est de degré 2. Le terme constant étant strictement négatif, φ admet deux racines réelles de signes stricts opposés.
∙ Il s’agit de montrer que φ admet une seule racine dans [0,1]. L’unicité résulte de ce qui
précède. En outre, φ(0) < 0 et φ(1) = ∥y - a∥2 - R2 ≥ 0 puisque y  F . Ceci montre
l’existence.
F . Ceci montre
l’existence.
∙ Puisque φ(tx,y ) = 0, on peut calculer tx,y grâce à l’égalité
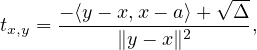
c) Posons h := ∥x - a∥. Alors
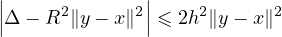
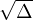 - R∥x - y∥|≤
- R∥x - y∥|≤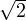 h∥x - y∥ grâce à l’inégalité
h∥x - y∥ grâce à l’inégalité
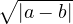 ≤
≤
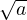 -
-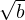
 pour a et b positifs ou nuls. On a donc
pour a et b positifs ou nuls. On a donc
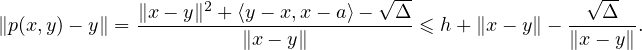
Comme |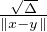 - R|≤
- R|≤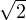 h,
h,
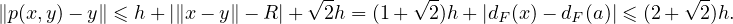
Le résultat annoncé en découle.
d) Donnons-nous un voisinage de π(a), que l’on suppose sans restriction de la forme
B(π(a), ϵ), avec ϵ > 0. D’après la question 27, il existe η > 0 tel que, si x  B(a,η),
alors Γ(x) ⊂ B(π(a),ϵ⁄2). D’après la question 28, il existe ηʹ > 0 tel que, pour tout
x
B(a,η),
alors Γ(x) ⊂ B(π(a),ϵ⁄2). D’après la question 28, il existe ηʹ > 0 tel que, pour tout
x  B(a, R) ∩ B(a,ηʹ), et pour tout y
B(a, R) ∩ B(a,ηʹ), et pour tout y  Γ(x), on ait ∥p(x,y) -y∥ < ϵ⁄2. Soit à présent x tel que
∥x - a∥ < min (R,η,ηʹ). Alors ∥p(x,y) - π(a)∥ < ϵ. C’est le résultat demandé.
Γ(x), on ait ∥p(x,y) -y∥ < ϵ⁄2. Soit à présent x tel que
∥x - a∥ < min (R,η,ηʹ). Alors ∥p(x,y) - π(a)∥ < ϵ. C’est le résultat demandé.
29. a) Il suffit d’écrire x - p(x,yx) = (x - a) + 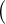 a - p(x,yx)
a - p(x,yx) et de développer le
carré.
et de développer le
carré.
b) On peut écrire
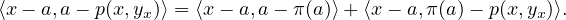
D’après la question 28, étant donné ϵ > 0, il existe η > 0 tel que, si ∥x - a∥ < η, alors
∥π(a) - p(x, yx )∥≤ ϵ. Pour ces valeurs de x,  ⟨x - a,π(a) - p(x,yx)⟩
⟨x - a,π(a) - p(x,yx)⟩ ≤ ϵ∥x - a∥. Donc
⟨x - a, π(a) - p(x,yx)⟩ = o(x - a) et finalement
≤ ϵ∥x - a∥. Donc
⟨x - a, π(a) - p(x,yx)⟩ = o(x - a) et finalement
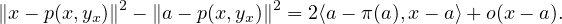
30. Puisque p(x,y)  [yx,x], on a ∥x - p(x,y)∥2 ≤ d(x,F)2. D’après la question 29, on en
déduit que
[yx,x], on a ∥x - p(x,y)∥2 ≤ d(x,F)2. D’après la question 29, on en
déduit que
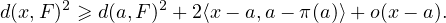
D’un autre côté, puisque π(a)  F , on a d(x,F)2 ≤∥x - π(a)∥2. Or
F , on a d(x,F)2 ≤∥x - π(a)∥2. Or
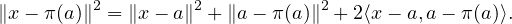
Par suite,
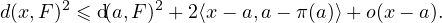
L’encadrement
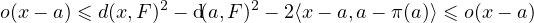
31. On vient de voir que d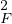 est différentiable en a, et que son gradient et 2(a-π(a)). Donc dF est
différentiable en a, et
est différentiable en a, et que son gradient et 2(a-π(a)). Donc dF est
différentiable en a, et
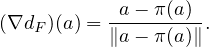
32. D’après ce qui précède, dF est différentiable en tout point de Ω. Il suffit de montrer que son
gradient est continu pour pouvoir affirmer que dF est de classe  1, ou encore de montrer que π est
continue sur Ω. Mais c’est justement le résultat de la question 26 appliquée au cas où Γ(x) est égal
au singleton {π(x)}.
1, ou encore de montrer que π est
continue sur Ω. Mais c’est justement le résultat de la question 26 appliquée au cas où Γ(x) est égal
au singleton {π(x)}.
Partie VII : une condition nécessaire de différentiabilité en un point de F
33. Si a est intérieur à F , dF est nulle dans un voisinage de a et donc son gradient en a est nul.
34. a) Par définition de la différentiabilité en a,
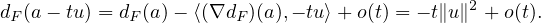
b) Pour t > 0, on obtient que -t∥u∥2 + o(t) ≥ 0 et, après division par t et tendaison de t vers 0,
que - ∥u∥2 ≥ 0. Donc u = 0.
[Table des matières]

