7047: Agregation Interne de Mathematiques, Deuxi`eme Epreuve 2020, enonce

[Table des matières]

Agrégation Interne de Mathématiques

Deuxième Épreuve 2020

7047Différentiabilité de la distance à une partie

Notations

On rappelle que l’on note N l’ensemble des entiers positifs ou nul, Z l’anneau des entiers relatifs, Q le corps des nombres rationnels, R le corps des nombres réels et C le corps des nombres complexes.
On se place dans un espace euclidien 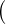E,⟨⋅,⋅⟩) de dimension n N^*. On note ∥.∥ la norme euclidienne associée.
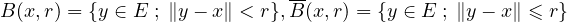
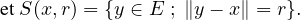
Pour tout vecteur x de E et tout réel positif r, on note B(x,r) (resp. B(x,r), resp. S(x, r)) la boule ouverte (resp. la boule fermée, resp. la sphère) de centre x et de rayon r : $-- B(x,r) = {y ∈ E ; ∥y- x∥ < r},B (x,r) = {y ∈ E ; ∥y - x∥ ≤ r}$ $etS(x,r) = {y ∈ E ; ∥y - x∥ = r}.$
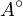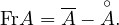
Pour toute partie A de E, on note l’intérieur de A, c’est-à-dire le plus grand ouvert (au sens de l’inclusion) inclus dans A, A l’adhérence de A, c’est-à-dire le plus petit fermé contenant A et FrA la frontière de A : $FrA = A-- •A.$
Si a est un élément de E, on note (a) l’ensemble des voisinages de a.
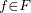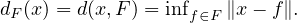
Pour toute partie fermée et non vide F de E et tout x E, on admet que l’ensemble ${∥x - f ∥}f∈F$ admet une borne inférieure notée inf ∥x - f∥ et on pose $dF(x) = d(x,F) = inff∈F ∥x - f∥.$
On pose alors Γ(x) = {f F ; ∥x - f∥ = d(x,F)}. C’est donc l’ensemble (éventuellement vide) des points de F pour lesquels la borne inférieure est atteinte.
Lorsque Γ(x) est un singleton, on note π(x) son unique élément.
Si u et v sont deux vecteurs de E, on appelle segment [u,v] l’ensemble défini par : $[u,v] = {x ∈ E ; ∃t ∈ [0,1] x = (1 - t)u + tv}.$
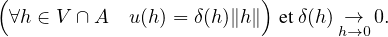
Soient A une partie de E et u : A → R. On suppose que 0 A. On dit que u(h) = _h→0o(∥h∥) lorsqu’il existe une fonction δ définie sur un voisinage V de 0 telle que $( ) ∀h ∈ V ∩A u(h) = δ(h)∥h ∥ etδ(h) →h→00.$
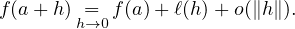
Soient Ω un ouvert de E et f : Ω → R. On rappelle que l’on dit que f est différentiable en un élément a de Ω lorsqu’il existe une forme linéaire l : E → R vérifiant : $f(a+ h)h=→0 f(a) + ℓ(h)+ o(∥h∥).$
Lorsqu’elle existe, l est unique et est notée df(a) et l’image l(h) du vecteur h de E par l est notée df(a) ⋅ h. Le gradient de f en a est alors l’unique vecteur v de E vérifiant :
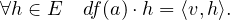
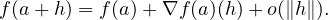
$∀h ∈ E df (a)⋅h = ⟨v,h⟩.$ On le note ∇f(a). Ainsi, sous réserve d’existence, on a : $f(a+ h) = f(a)+ ∇f(a)(h)+ o(∥h ∥).$
Pour tout réel x, on note ⌊x⌋ sa partie entière.

Le problème a pour objectif d’étudier la différentiabilité de la fonction d_F : x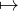d(x,F) en fonction de la partie F .

On fixe donc une partie F de E non vide et fermée.

Partie I — Résultats préliminaires

1.

Montrer que, pour tout vecteur x de E, d_F(x) = 0 si et seulement si x

F .

2.

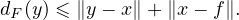
(a): Montrer que, pour tout (x,y) E² et tout f F , on a : $dF(y) ≤ ∥y- x∥ + ∥x- f∥.$
(b): En déduire que d_F est 1-lipschitzienne.

3.

Soient x un vecteur de E et x₀ un vecteur de F . On pose r := ∥x-x₀∥ et K := B(x,r) ∩F .

(a): Montrer que K est une partie compacte et non vide de E.
(b): Montrer que Γ(x) est non vide.

4.

On suppose, dans cette question seulement, que F est de plus une partie convexe de E.

(a)

Montrer que, quels que soient les vecteurs u et v de E, on a

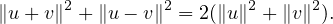
2 2 2 2 ∥u +v∥ + ∥u- v∥ = 2(∥u∥ + ∥v∥ ).

(b)

Soit x un vecteur de E et soient f et fʹ deux éléments de Γ(x). On suppose que f≠ fʹ. Montrer que : ∥ 1
2

(f + fʹ) - x∥² < d(x,F)².

En déduire que, pour tout vecteur x de E, Γ(x) est un singleton. Ainsi, avec les notations de l’introduction, Γ(x) = {π(x)}.

(c)

On souhaite montrer que

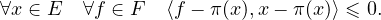
∀x ∈ E ∀f ∈ F ⟨f - π(x),x - π(x)⟩ ≤ 0.

Pour cela, on fixe des éléments x de E et f de F . On introduit la fonction

{ [0,1] -→ R φ : 2 t ↦-→ ∥(1 - t)π(x)+ tf - x∥ .

i.: Montrer que φ est une fonction polynomiale de degré inférieur ou égal à 2.
ii.: Justifier que φ admet un minimum en 0. Conclure.

(d)

On fixe un vecteur x de E. Soit z un vecteur de F . On suppose que :

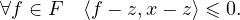
∀f ∈ F ⟨f - z,x- z⟩ ≤ 0.

Montrer que z = π(x).

Partie II — Étude en dimension 1

On suppose, dans toute cette partie, que E = R, et que R est muni de sa structure euclidienne canonique.

1.: Expliciter d_{0}, puis déterminer l’ensemble des points où d_{0} est dérivable et déterminer sa dérivée.

Dans les questions à , on suppose que F = Z et on étudie donc la fonction d_Z.

1.

Montrer que Z est fermé dans R.

2.

Justifier que d_Z est 1-périodique. Étudier la parité.

3.

Pour tout x élément de [0,1[, expliciter, en justifiant, d_Z(x) en fonction de x. Tracer le graphe de d_Z.

4.

Étudier la dérivabilité de d_Z en tout point de [0,1[.

5.

Développement en série de Fourier de d_Z.

(a): Calculer les coefficients de Fourier de d_Z.
(b): La série de Fourier de d_Z converge-t-elle simplement/uniformément/normalement vers d_Z ?
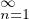
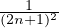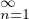
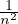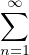
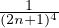(c): En déduire la valeur de puis de , de et de .
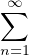
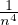On commencera par justifier la convergence des séries.

Pour toute la suite de la partie, on fixe une partie fermée F de R. On note Ω le complémentaire de F. C’est donc une partie ouverte de R.

1.

On définit, sur Ω, une relation binaire ~ de la manière suivante : étant donnés deux éléments x et y de Ω, on dit que x est en relation avec y lorsqu’il existe un intervalle ouvert ]a,b[

inclus dans Ω et contenant les éléments x et y :

2 ( ( 2 2 )) ∀(x,y)∈ Ω x ~ y ⇔ ∃(a,b) ∈ R (a < bet(x,y) ∈ ]a,b[ et ]a,b[ ⊂ Ω ) .

(a): Montrer que ~ est une relation d’équivalence.
(b): Montrer que les classes d’équivalences sont des intervalles ouverts deux à deux disjoints.
(c): En déduire qu’il existe une famille ()_iI d’intervalles ouverts deux à deux disjoints, indexée par un ensemble I fini ou dénombrable, telle que $⋃ Ω = ]ai,bi[. i∈I$

2.

Soit x un élément de Ω. Il existe donc un unique i₀ élément de I tel que x

(a): Exprimer d_F(x) à l’aide de x, de a_i₀ et b_i₀.
(b): Étudier la dérivabilité de d_F en x.

3.

On suppose dans cette question que

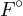≠∅. Soit x un élément de F •

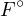. Étudier la dérivabilité de d_F en x.

4.

Étude à la frontière.

(a)

On suppose, dans cette question, que F = [0,1]. Expliciter FrF . La fonction d_F est-elle dérivable en un point de FrF ?

(b)

Dans cette question, on pose : F = R\Ω où Ω = ⋃ _n≥2

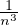, la réunion étant prise sur l’ensemble des entiers naturels n tels que n ≥ 2.

i.: Justifier rapidement que Ω ⊂ , que F est un fermé de R et que 0 FrF .
ii.: Soit x Ω. Montrer qu’il existe un unique entier naturel n tel que n ≥ 2 et x . Montrer que n = .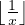
iii.: En déduire qu’il existe un réel C strictement positif tel que $] 1[ ∀x ∈ 0,2 ,dF (x ) ≤ Cx3.$
iv.: Montrer que d_F est dérivable à droite en 0 et calculer (d_F)ʹ_d(0).
v.: La fonction d_F est-elle dérivable en 0 ?

Partie III — Étude de cas particuliers en dimension n

1.

On fixe un vecteur x₀

E et on suppose, dans cette seule question, que F = {x₀}.

(a)

Expliciter d_F. Soit x un élément de E. Expliciter Γ(x).

(b)

Montrer que la fonction g: {
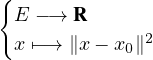E -→ R
x ↦-→ ∥x- x0∥2

est différentiable sur E et calculer son gradient.

(c)

En déduire que d_F est différentiable sur E\{x₀} et montrer que :

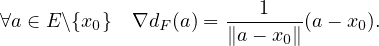
∀a ∈ E \{x0} ∇dF(a) = ---1---(a- x0). ∥a- x0∥

(d)

Étude de la différentiabilité de d_F en x₀. Supposons que d_F est différentiable en x₀ .

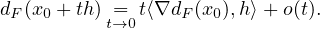
i.: Montrer que, pour tout vecteur h de E, on a : $dF (x0 + th) = t⟨∇dF (x0),h⟩+ o(t). t→0$
ii.: Conclure.

2.

On suppose, dans cette question seulement, que F est un sous-espace vectoriel de E, distinct de E.

(a)

Montrer que pour tout vecteur x de E, Γ(x) est un singleton, et que π (défini dans le préambule du sujet) est le projecteur orthogonal sur F .

(b)

Montrer que, pour tout élément a de E, d

est différentiable en a et calculer son gradient.

(c)

En déduire que, pour tout élément a de E\F , d_F est différentiable en a et calculer son gradient.

(d)

On fixe un vecteur a de F . L’objet de cette question est l’étude de la différentiabilité de d_F en a.

i.: On suppose que d_F est différentiable en a et on pose : u = ∇(d_F)(a).
Soit h F^⊥. Montrer que : ⟨u,h⟩ = ∥h∥.
Indication : on pourra procéder de manière analogue à la question .
ii.: Conclure.

3.

Dans cette question, on suppose E = R² (ses éléments sont notés en colonne) muni de sa structure euclidienne canonique et F =

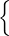
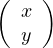
R² ; y ≤ 0 ou y ≥ x²

. L’objet de cette question est d’étudier la différentiabilité de d_F en 0_R².

(a): Dessiner l’allure de F .
(b): Montrer que F est un fermé de R².
(c): Montrer que 0_R² FrF .
(d): Montrer que, pour tout vecteur u de R², d_F(u) ≤∥u∥².
Indication : on pourra séparer les cas où u F et où u R²\F .
(e): En déduire que d_F est différentiable en 0_R² et donner son gradient en 0_R².

Partie IV — Distance à la sphère unité

On suppose, dans cette partie seulement, que : F = {x E;∥x∥ = 1}. C’est donc la sphère de centre 0_E et de rayon 1.

1.

Soit a un élément de E\{0_E}. On pose u = 1
---
∥a∥

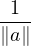a et on fixe un vecteur y de F.

(a): Montrer qu’il existe un plan vectoriel contenant a, u et y.
(b): Montrer que S = F ∩ 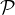est le cercle unité de 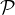, pour la structure euclidienne sur 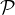induite par celle de E.
(c): Montrer que Γ(a) = {u}.

2.

Montrer que, pour tout vecteur a de E : d_F(a) = |
|

∥a∥- 1

3.

Montrer que, pour tout vecteur a de E tel que a≠0_E et a

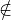F , d_F est différentiable en a et calculer son gradient.

4.

Expliciter Γ(0_E).

5.

Soit a un vecteur de F . Montrer que d_F n’est pas différentiable en a.

Indication : On pourra calculer d_F(a + ta), pour tout t élément de ]- 1,1[ .

6.

On fixe un vecteur unitaire v.

(a): Étudier la dérivabilité en 0 de φ: .
(b): Conclure quant à la différentiabilité de d_F en 0.

Partie V — Une condition nécessaire de différentiabilité à l’extérieur de F

Dans cette partie, on fixe un vecteur a de E\F et on suppose d_F est différentiable en a.

On souhaite montrer qu’alors :

1 Γ(a)estunsingletonetque∇dF (a) = d-(a)(a - π(a)). F

On pose u = ∇d_F(a).

1.

(a): Montrer que, pour tout t > 0, d_F(a + tu) - d_F(a) ≤ t∥u∥.
(b): En déduire que ∥u∥≤ 1.

Dans la suite de cette partie, on se donne un élément y de Γ(a).

1.

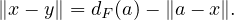
(a): Montrer que pour tout x [a,y], $∥x- y∥ = dF(a)- ∥a- x∥.$
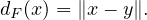
(b): En déduire que pour tout x [a,y], $dF(x) = ∥x - y∥.$

2.

On fixe t

]0,d_F(a)] et on pose v = --1--
dF(a)

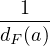(a - y).

(a): Montrer que d_F(a - tv) = d_F(a) - t.
(b): Montrer que ⟨u,v⟩ = 1 = ∥u∥∥v∥.
(c): En déduire que u = v et conclure.

Partie VI — Étude de la réciproque

Dans cette partie, on fixe a E\F et on suppose que Γ(a) est un singleton. Ainsi, avec les notations du préambule,

Γ (a) = {π(a)}.

On souhaite montrer que d_F est différentiable en a et que ∇(d_F)(a) = 1
dF(a)

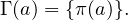
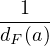(a - π(a)).

1.

Dans cette question, on se propose de montrer que :

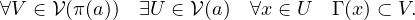
∀V ∈ V(π(a)) ∃U ∈ V (a) ∀x ∈ U Γ (x) ⊂ V.

On va l’établir à l’aide d’un raisonnement par l’absurde. On suppose donc qu’il existe un voisinage ouvert V de π(a) tel que :

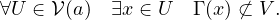
∀U ∈ V (a) ∃x ∈ U Γ (x) ⁄⊂ V .

On dispose ainsi d’une suite (x_p)_pN convergeant vers a et d’une suite (y_p)_pN telles que :

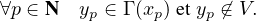
∀p ∈ N yp ∈ Γ (xp) etyp ⁄∈ V.

On pose : M = sup p∈N

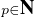∥x_p - a∥.

(a): Justifier succinctement que M est bien défini, puis montrer que (y_p)_pN est bornée.

On note l une valeur d’adhérence de (y_p)_pN.

(a): Justifier succinctement l’existence de l.
(b): Montrer que l F ∩ (E\V ).
(c): Montrer que l Γ(a), puis conclure.

2.

On pose : R = ∥a - π(a)∥.

(a)

Justifier que R > 0 et expliciter B(a,R) ∩ F .

(b)

Soit x un élément de B(a,R). On fixe un élément y de Γ(x).

On considère la fonction φ: {
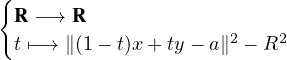R -→ R
t ↦- → ∥(1- t)x + ty- a∥2 - R2 .

i.: Montrer que ϕ est un trinôme du second degré. Que dire du signe des racines de ce trinôme ?
ii.: Montrer que [x,y] ∩ S(a,R) est un singleton. On note p(x,y) le point d’intersection.
Il existe donc un unique t_x,y [0,1] vérifiant : p(x,y) = (1-t_x,y)x+t_x,yy.
iii.: Que vaut φ(t_x,y) ? En déduire une expression de t_x,y.

(c)

Montrer que :

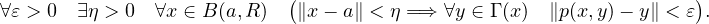
( ) ∀ε>0 ∃η > 0 ∀x ∈ B (a,R) ∥x- a∥ < η =⇒ ∀y ∈ Γ (x) ∥p(x,y)- y∥ < ε .

(d)

En déduire que :

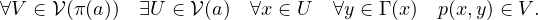
∀V ∈ V (π(a)) ∃U ∈ V(a) ∀x ∈ U ∀y ∈ Γ (x ) p(x,y) ∈ V.

3.

Soit x élément de B(a,R) ; on note y_x un élément de Γ(x). Montrer que, pour tout x

B(a, R),

(a): ∥x - p(x,y_x)∥² -∥a - p(x,y_x)∥² = 2⟨x - a,a - p(x,y_x)⟩ + ∥x - a∥² ;
(b): ∥x - p(x,y_x)∥² -∥a - p(x,y_x)∥² =_x→a2⟨x - a,a - π(a)⟩ + o(∥x - a∥).

4.

Montrer que : d 2
F

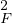(x)=_x→ad

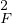(a) + ⟨x - a,2(a - π(a))⟩ + o(∥x - a∥).

5.

En déduire que d_F est différentiable en a et calculer son gradient.

6.

Soit Ω un ouvert inclus dans E\F . On suppose que, pour tout x

Ω, Γ(x) est un singleton. Montrer que d_F est de classe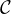

¹ sur Ω.

Partie VII — Une condition nécessaire de différentiabilité en un point de F

Dans cette partie, on fixe un élément a de F et on suppose que d_F est différentiable en a. On souhaite montrer que : ∇(d_F)(a) = 0. On pose encore : u = ∇(d_F)(a).

1.

Montrer le résultat dans le cas où a

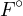2.

On se place dans le cas où a

FrF .

(a): Montrer que : d_F(a - tu)=_t→0 - t∥u∥² + o(t).
(b): Conclure.

[Table des matières]

[ < ]

Recherche, Affichage et Navigation

Les numéros