[Table des matières]
Agrégation Interne de Mathématiques
Première Épreuve 2020
7046Décomposition de Bruhat.
Corrigé par Alain Tissier, comité de rédaction de la RMS
Dans la partie I on étudie pour un endomorphisme d’un espace vectoriel le lien entre la
trigonalisation et la stabilité des drapeaux. Dans la partie II on introduit la notion de
groupe-quotient, puis de double classe d’un groupe G selon un couple (H,K) de deux sous-groupes
de G. Dans la partie III on étudie la décomposition de Bruhat d’un automorphisme d’un espace
vectoriel, puis les doubles classes de GLn(K) selon (H,H) où H est le sous-groupe T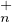 (K) des
matrices triangulaires supérieures inversibles. Dans la partie IV on étudie l’action du groupe
GLn(K ) dans l’ensemble quotient GLn(K)⁄(T
(K) des
matrices triangulaires supérieures inversibles. Dans la partie IV on étudie l’action du groupe
GLn(K ) dans l’ensemble quotient GLn(K)⁄(T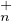 (K))2.
(K))2.
Partie I : drapeaux de sous-espaces vectoriels
1. Par construction chaque Ei est un sous-espace vectoriel de E qui est de dimension i. Pour i < n, puisque Ei ⊕ V ect(ei+1) = Ei+1, Ei est inclus strictement dans Ei+1. Ainsi, Ei est un drapeau. Comme l’entier p de la définition vaut n, on voit que (Ei)0≤i≤n est, par définition, un drapeau total. Donc (Ei)1≤i≤n est un drapeau total de E.
2. On a dim Ei > dimEi-1 pour tout i de 1 à n. On en déduit pour tout i : dimEi ≥ i mais aussi n = dim E ≥ n - i + dimEi donc dimEi = i. Soit, pour tout i de 1 à n, ei un élément de Ei non situé dans Ei-1. Par récurrence sur i, (e1,e2,…,ei) est un système libre de i vecteurs de Ei et est donc une base de Ei pour tout i. En particulier (e1,e2,…,en) est une base de E, adaptée au drapeau total (Ei) car V ect(e1,…,ei) = Ei pour tout i.
3. On reprend la question précédente. Pour 1 ≤ i ≤ n, comme Ei-1 est un hyperplan de Ei, son orthogonal dans Ei est une droite vectorielle dans laquelle on peut choisir un vecteur unitaire ei. On obtient ainsi une base adaptée qui est de surcroît orthonormée.
4. Soit 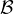 = (e1 , e2,…,en) une base de E constituée de vecteurs propres de u. Pour tout i,
Ei = V ect (e1 , e2 ,…,ei) est stable par u car c’est une somme de i droites stables par u. Donc
= (e1 , e2,…,en) une base de E constituée de vecteurs propres de u. Pour tout i,
Ei = V ect (e1 , e2 ,…,ei) est stable par u car c’est une somme de i droites stables par u. Donc 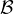 est
une base adaptée à un drapeau total de E.
est
une base adaptée à un drapeau total de E.
5. a) Notons Xk la famille (un-1(x),un-2(x), ,un-k(x))
,un-k(x))
Montrons par récurrence sur k, élément de [[1,n]], que Xk est libre.
C’est vrai pour k = 1 puisque X1 = (un-1(x)) est consituée d’un vecteur non nul.
Supposons 1 ≤ k ≤ n - 1 et Xk libre.
Par l’absurde, étant constituée de Xk et de un-k+1(x), si Xk+1 n’est pas libre, on peut trouver des
scalaires a1 , … , ak tels que un-k-1(x) = a1un-1(x) + a2un-1(x) +  + akun-k(x).
+ akun-k(x).
Composons les deux membres par u : un-k(x) = a2un-1(x) + a3un-1(x) +  + akun-k+1(x).
Ceci contredit la liberté de Xk.
+ akun-k+1(x).
Ceci contredit la liberté de Xk.
b) En particulier Xn = (un-1(x),un-2(x), ,u(x),x) est un système libre de n vecteurs, donc
une base de E.
,u(x),x) est un système libre de n vecteurs, donc
une base de E.
Pour tout i, u envoie les vecteurs de Xi sur ceux de Xi-1 et 0, donc u(Xi) = Xi-1 ; comme Xi-1 est inclus dans Xi le drapeau des Ei est stable par u. La base Xn est donc adaptée au drapeau total donné par Ei = V ect(Xi) pour 0 ≤ i ≤ n.
Soit y dans E ; il s’écrit de façon unique y = 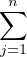 ajun-j(x) pour certains réels aj. Puis
ui (y) =
ajun-j(x) pour certains réels aj. Puis
ui (y) = 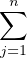 ajun+i-j(x) =
ajun+i-j(x) = 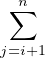 ajun+i-j(x) =
ajun+i-j(x) = 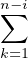 ai+kun-k(x).
ai+kun-k(x).
Cette égalité montre que ui(y) est nul si et seulement si aj = 0 pour tout j compris entre i + 1 et n, c’est-à-dire que y est dans Ei. Donc Ei = Kerui pour tout i.
Ainsi (Ker ui )0≤i≤n est un drapeau total de E stable par u ; une base adaptée à ce drapeau est (un-i (x))1≤i≤n , car pour tout i, un-i(x) est dans Ei sans être dans Ei-1.
6. Si u est trigonalisable, on dispose une base (e1,e2,…,en) telle que u(ei) est pour tout i combinaison linéaire de e1,e2,…,ei.
Notons Ei = V ect(e1,e2,…,ei) pour 1 ≤ i ≤ n et E0 = {0}. Alors (Ei)0≤i≤n est un drapeau total.
Pour 1 ≤ i ≤ j ≤ n, u(ei) est dans Ej donc u(Ej) ⊂ Ej pour tout j. Ainsi u stabilise le drapeau
total (Ej ).
Réciproquement si u stabilise un drapeau total (Ei), on introduit une base (ei) adaptée à (Ei). Pour tout i, u(Ei ) ⊂ Ei, donc u(ei) est dans Ei = V ect(e1,…,ei) et u est trigonalisée dans la base (ei ).
7. D’après la question 6., u stabilise un drapeau total (Ei) ; d’après la question 3. il existe une base orthonormée adaptée à ce drapeau. Ainsi u se trigonalise dans cette base orthonormée.
Partie II : des groupes quotients
8. Vérifions d’abord la cohérence de la définition.
Supposons g1 H = gʹ1H et g2H = gʹ2H et montrons (g1g2)H = (gʹ1gʹ2)H.
En effet la relation (gH = gʹH) équivaut à (g-1gʹ H). Par hypothèse h1 = g
H). Par hypothèse h1 = g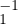 gʹ1 et
h2 = g
gʹ1 et
h2 = g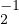 gʹ2 sont des éléments de H. Puis (g1g2)-1gʹ
1gʹ2 = g
gʹ2 sont des éléments de H. Puis (g1g2)-1gʹ
1gʹ2 = g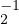 h1gʹ2 = (g
h1gʹ2 = (g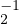 h1g2)h2.
Comme le sous-groupe H est distingué dans G, g
h1g2)h2.
Comme le sous-groupe H est distingué dans G, g h1g2 est un élément h3 de H et
h1g2 est un élément h3 de H et
(g1 g2 )-1 gʹ1 gʹ2 = h3h2 est bien dans H.
L’application π : g gH est donc bien définie et est par construction un morphisme surjectif de G
sur (G⁄H, *). Comme G est un groupe, * est donc une loi de groupe sur G⁄H. L’élément neutre est
1G H = H.
gH est donc bien définie et est par construction un morphisme surjectif de G
sur (G⁄H, *). Comme G est un groupe, * est donc une loi de groupe sur G⁄H. L’élément neutre est
1G H = H.
9. L’ensemble T (K) est un sous-groupe de GLn(K) dont les éléments sont les matrices
triangulaires supérieures à éléments diagonaux non nuls. De plus, pour tous V,W de T
(K) est un sous-groupe de GLn(K) dont les éléments sont les matrices
triangulaires supérieures à éléments diagonaux non nuls. De plus, pour tous V,W de T (K), pour
tout indice i, on a (V W)[i,i] = V [i,i]W[i,i] ; V -1[i,i] =
(K), pour
tout indice i, on a (V W)[i,i] = V [i,i]W[i,i] ; V -1[i,i] = ![-1--
V[i,i]](/numeros/RMS130-4/RMS130-4373x.png) .
.
a) D’après ce qui précède, étant l’ensemble des U de T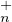 (K) telles que U[i,i] = 1 pour tout i,
TU
(K) telles que U[i,i] = 1 pour tout i,
TU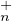 (K ) contient In et est stable pour le produit et le passage à l’inverse. C’est donc un
sous-groupe de T
(K ) contient In et est stable pour le produit et le passage à l’inverse. C’est donc un
sous-groupe de T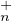 (K).
(K).
Pour tout U de TU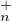 (K) et tout V de T
(K) et tout V de T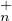 (K), pour tout indice i, on a, d’après le préambule :
(V -1 UV )[i, i] = 1 ; ainsi V -1UV est dans TU
(K), pour tout indice i, on a, d’après le préambule :
(V -1 UV )[i, i] = 1 ; ainsi V -1UV est dans TU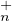 (K).
(K).
Donc le sous-groupe TU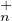 (K) est distingué dans T
(K) est distingué dans T (K).
(K).
b) Réponse NON si n ≥ 2.
L’ensemble des P-1UP où P est inversible et U est dans TU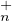 (K) est l’ensemble des matrices
trigonalisables ayant 1 pour unique valeur propre. Cet ensemble n’est pas inclus dans TU
(K) est l’ensemble des matrices
trigonalisables ayant 1 pour unique valeur propre. Cet ensemble n’est pas inclus dans TU (K) ; il
contient par exemple toutes les matrices triangulaires inférieures dont la diagonale ne contient que
des 1.
(K) ; il
contient par exemple toutes les matrices triangulaires inférieures dont la diagonale ne contient que
des 1.
10. Soit g un élément de G. Si g est dans H alors Hg = gH = H. Sinon G = H ⊔gH = H ⊔Hg, donc Hg = gH = G \ H. Ainsi gH = Hg pour tout g de G et H est distingué dans G.
11. a) Puisque A et B sont inversibles, elles engendrent un sous-groupe < A,B > de GL2.
On vérifie A2 = -I2 et B2 = I2.
Le groupe < A > est cyclique d’ordre 4, il est constitué des éléments distincts I2, A, -I2 = A2, - A = A3 .
Le groupe < B > est de cardinal 2 ; il est constitué des éléments distincts I2 et B.
Le groupe < A, B > inclut < A > et < A > B ; ce sont des ensembles disjoints puisque B n’appartient pas à < A >. Leur réunion est Δ.
On vérifie AB = C où C = 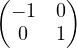 et BA = -C. Puis A3B = -AB = BA.
et BA = -C. Puis A3B = -AB = BA.
On a BA = A-1 B, puis BAkB-1 = A-k.
Ces formules pemettent d’affirmer que Δ est stable pour le produit.
En effet : Ai Aj = Ai+j ; (Ai)(AjB) = Ai+jB ; (AiB)(Aj) = Ai-jB ; (AiB)(AjB) = Ai-j.
De plus Δ est stable par passage à l’inverse : (Ai)-1 = A-i et (AiB)-1 = AiB.
Ainsi Δ est un sous-groupe de GL2.
b) On a vu : Δ = Γ ⊔ ΓB où Γ =< A >. D’après 10., Γ est un sous-groupe distingué de Δ. Le groupe quotient Δ⁄Γ est de cardinal 2 et isomorphe à tout groupe cyclique d’ordre 2 en particulier R =< B >.
c) Γ × R est commutatif puisqu’il est le produit de deux groupes cycliques. Par contre Δ n’est pas commutatif car BA = A-1B≠AB. Il n’existe donc aucun isomorphisme entre ces deux groupes.
12. a) L’ensemble HgK est la réunion des aK où a est dans Hg et c’est aussi la réunion des Hb où b est dans gK.
b) Supposons non vide l’intersection Hg1K ∩ Hg2K. Alors h1g1k1 = h2g2k2 pour certains h1 , h2 de H et k1 ,k2 de K. Mais Hh1g1k1K = Hg1K et Hh2g2k2K = Hg2K donc Hg1 K = Hg2 K. Ainsi deux doubles classes sont ou bien disjointes ou bien identiques. Elles constituent donc une partition de G.
Partie III : décomposition de Bruhat et matrices
13. Comme uσ transporte une base sur une base, uσ est dans GLn(K).
Soit σ et τ des éléments de 𝔖n ; pour tout indice j on a uσ(uτ(εj)) = uσ(ετ(j)) = εσ(τ(j)) = ε(στ)(j)). On en tire : uσ uτ = uστ.
La représentation matricielle étant un isomorphisme, σ Pσ est un morphisme de 𝔖n dans
GLn(K ). Si Pσ = In alors σ = id. Donc σ
Pσ est un morphisme de 𝔖n dans
GLn(K ). Si Pσ = In alors σ = id. Donc σ Pσ est un isomorphisme de 𝔖n sur un sous-groupe
de GL n (K ), le groupe des matrices de permutation.
Pσ est un isomorphisme de 𝔖n sur un sous-groupe
de GL n (K ), le groupe des matrices de permutation.
Tout coefficient de Pσ vaut 0 ou 1 et Pσ[i,j] = 1 si et seulement si i = σ(j).
a) Ici uσ (ej ) = ej+1 pour 1 ≤ j ≤ n - 1 et uσ(en) = e1. Notons Qn = Pσ. On a
Qn [1, n] = Qn [2,1] =  = Qn[n,n - 1] = 1, les autres Qn[i,j] étant nuls.
= Qn[n,n - 1] = 1, les autres Qn[i,j] étant nuls.
Ainsi Qn = 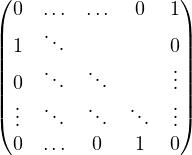 .
.
b) En renumérotant les éléments de la base de façon que c1 = [1,2,…,n1],
c2 = [n1 + 1, n1 + 2,…,n1 + n2], . . ., ck = [n1 +  + nk-1 + 1,…,n1 +
+ nk-1 + 1,…,n1 +  + nk], on obtient
la matrice diagonale par blocs Diag(Qn1,…,Qnk) où Qn est définie dans la question
précédente.
+ nk], on obtient
la matrice diagonale par blocs Diag(Qn1,…,Qnk) où Qn est définie dans la question
précédente.
c) La matrice Pσ est réelle. Chacune de ses colonnes est un vecteur de la base canonique et est donc de norme 1. Deux colonnes distinctes sont deux vecteurs distincts de cette base qui sont orthogonaux. Le système des colonnes de Pσ est une base orthonormée de Rn. On retrouve une des définition des matrices orthogonales.
d) D’après la formule des déterminants, detPσ = 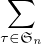 s(τ)
s(τ)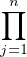 Pσ[τ(j),j] où s est la signature.
Le seul terme non nul de cette somme est indexé par σ et vaut s(σ). Donc detPσ est la
signature de σ. Ainsi Pσ est dans SOn(R) si et seulement si s(σ) = 1, c’est-à-dire si σ est
paire.
Pσ[τ(j),j] où s est la signature.
Le seul terme non nul de cette somme est indexé par σ et vaut s(σ). Donc detPσ est la
signature de σ. Ainsi Pσ est dans SOn(R) si et seulement si s(σ) = 1, c’est-à-dire si σ est
paire.
14. On notera Lu(A) la u-ième ligne de A et Cv(A) la v-ième colonne de A.
a) Posons B = Ti,j(λ)A.
On a B = (In + λEi,j)A = A + λ A[j,v]Ei,v. Donc B[u,v] = A[u,v] si u≠i et
B[i, v] = A[i, v] + λA[j,v].
A[j,v]Ei,v. Donc B[u,v] = A[u,v] si u≠i et
B[i, v] = A[i, v] + λA[j,v].
Ainsi Li (B) = Li(A) + λLj(A) et Lu(B) = Lu(A) si u≠i.
b) Posons B = Di(λ)A.
On a B = A + (λ - 1) A[i,v]Ei,v.
A[i,v]Ei,v.
Donc Li (B) = λLi(A) et Lu(B) = Lu(A) si u≠i.
Posons B = ATi,j(λ).
On a B = A(In + λEi,j) = A + λ A[u,i]Eu,j. Donc B[u,v] = A[u,v] si v≠j et
B[u, j] = A[u, j] + λA[u,i].
A[u,i]Eu,j. Donc B[u,v] = A[u,v] si v≠j et
B[u, j] = A[u, j] + λA[u,i].
Ainsi Cj (B) = Cj(A) + λCi(A) et Cv(B) = Cj(A) si v≠j.
Pour B = ADi (λ), Cv(B) = Cv(A) si v≠j et Cj(B) = λCj(A).
c) L’opération A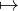 Pi,jA échange Li(A) et Lj(A). L’opération A
Pi,jA échange Li(A) et Lj(A). L’opération A Pi,jA échange Ci(A) et
Cj (A). Toute permutation se décompose en produit de transpositions, donc Pσ est un produit de
Pi,j . En obtient PσA (resp. APσ) en effectuant des multiplications successives de A par ces Pi,j à
gauche (resp. droite).
Pi,jA échange Ci(A) et
Cj (A). Toute permutation se décompose en produit de transpositions, donc Pσ est un produit de
Pi,j . En obtient PσA (resp. APσ) en effectuant des multiplications successives de A par ces Pi,j à
gauche (resp. droite).
15. On a Pσ-1 [i,j] = 1 si et seulement si j = σ(i). On en déduit : Pσ-1A[i,j] = A[σ(i),j].
On a Pσʹ [i, j] = 1 si et seulement si i = σʹ(i). On en déduit : APσʹ[i,j] = A[i,σʹ(j)].
Ainsi V [i, j] = Pσ-1UPσʹ[i,j] = U[σ(i),σʹ(j)].
En particulier V [i,i]≠0 ce qui force σ(i) ≤ σʹ(i) pour tout i, puis σʹ(σ-1(k)) ≥ k pour tout k ; donc σʹ(σ-1 (n) = n puis σʹ(σ-1(k) = k pour tout k par récurrence descendante. Ainsi σʹσ-1 = id et σʹ = σ.
16. a) On va construire par récurrence une pemutation σ de [[1,n]] et une suite de matrices
(U1 ,  , Un ), où Uj est dans TU
, Un ), où Uj est dans TU (K), telles que la suite de matrices (A0,A1,
(K), telles que la suite de matrices (A0,A1, ,An) donnée
par A0 = A puis UjAj = Aj-1 pour tout j de 1 à n vérifie les propriétés suivantes :
,An) donnée
par A0 = A puis UjAj = Aj-1 pour tout j de 1 à n vérifie les propriétés suivantes :
- Av [i, j] = Aj[i,j] pour tout v ≥ j ;
- Aj [i, j] = 0 pour tout i autre que σ(1),…,σ(j - 1).
- Aj [σ(j), j]≠0.
Soit 1 ≤ j ≤ n. Supposons ou bien j = 1 ou bien que sont construits σ(1),…σ(j - 1) et U1 , … , Uj-1 .
La matrice Aj-1 est inversible ; elle a d’ailleurs même déterminant que A. En particulier la j-ème colonne de Aj-1 n’est pas combinaison linéaire des j - 1 premières ; or ces j - 1 premières colonnes sont combinaisons linéaires de Eσ(1), . . ., Eσ(j-1) et engendrent un espace vectoriel de dimension j - 1, qui est donc V ect(Eσ(1),…,Eσ(j-1).
Ainsi la j-ème colonne de Aj possède au moins un coefficient non nul d’indice i autre que σ(1), . . ., σ(j - 1); on note σ(j) le plus grand d’entre eux.
On effectue, pour tout i < σ(j), les opérations Li ← Li -![A[i,j]
A[σ(j),j]](/numeros/RMS130-4/RMS130-4401x.png) Lσ(j).
Lσ(j).
Ces opérations ne modifient en rien les j - 1 premières colonnes (puisqu’elles possèdent un 0 sur la ligne pivot). La nouvelle j-ième colonne a des 0 sur toutes les lignes d’indice autre que σ(1), … , σ(j - 1) et un coefficient non nul sur la σ(j)-ième ligne.
La matrice Uj est la matrice triangulaire supérieure In +  1≤i<σ(j)
1≤i<σ(j)![-A-[i,j]
A[σ(j),j]](/numeros/RMS130-4/RMS130-4403x.png) Ei,σ(j).
Ei,σ(j).
Par construction An = PσV , où pour tout j la j-ième ligne de V est la σ(j)-ième ligne de An. Par construction V [j, j]≠0 pour tout j et V (i,j) = 0 si i > j. Donc V est triangulaire supérieure inversible.
On obtient ainsi : A = UPσV où U est la matrice U1U2…Un et qui est dans TU (K).
(K).
Remarquons qu’il n’est pas nécessaire, à chaque pas de remplacer par 0 tous les coefficients de la j-ième colonne d’indice i < σ(j) ; il suffit de le faire pour tous ceux de ces i qui diffèrent de σ(1), … , σ(j - 1).
b) Soit A = UPσV = UʹPσʹV ʹ où U,Uʹ sont triangulaires supérieures avec des 1 sur la diagonale et V, V ʹ sont triangulaires supérieures inversibles. Alors Pσ-1UʹʹPσʹ = V ʹʹ où Uʹʹ = U-1Uʹ et V ʹʹ = V V ʹ-1 sont triangulaires supérieures inversibles. On retrouve la situation de 15.. On a σʹ = σ.
Ainsi σ est bien déterminée par A.
Remarque. Cette preuve n’utilise pas le fait que U et Uʹ ont des diagonales de 1. Elles peuvent être
des éléments quelconques de T (K).
(K).
17. Si c = 0, alors σ = id. Une décomposition est A = I2I2A.
Si c≠ 0, on trouve la décomposition A = 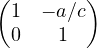
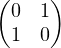
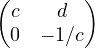 .
.
18. On notera systématiquement, pour tout entier k > 0 et pour toute matrice carrée M, M(k) sous-matrice de M donnée par les k premières valeurs des indices de ligne et de colonne. La même notation s’appliquera aux vecteurs-lignes et aux vecteurs-colonnes.
Le mineur principal d’indice k de M est donc detM(k).
a) Si A vérifie (E1) alors A est le produit de deux matrices inversibles et A est inversible.
Comme det A = detA(n), si A vérifie (E2), alors A est inversible.
b) On suppose A = LU où L est triangulaire inférieure inversible et V est triangulaire supérieure inversible.
Soit k un indice compris entre 1 et n - 1. On décompose toute matrice n × n en blocs :
M = 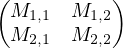 où M1,1 = M(k).
où M1,1 = M(k).
On a 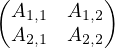 =
= 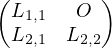
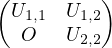 . La lettre O désigne la matrice nulle de
n’importe quel format.
. La lettre O désigne la matrice nulle de
n’importe quel format.
On en déduit en particulier A1,1 = L1,1U1,1. Or detL = detL1,1L2,2≠0 ; detU = detU1,1U2,2≠0. Donc det L1,1 ≠ 0 detU1,1≠0, detA1,1 = detL1,1 detU1,1≠0.
Ainsi det A(k) n’est pas nul. C’est vrai pour tout k de [[1,n]].
Donc si A vérifie (E1), alors A vérifie (E2).
c) On suppose non nul detA(k) pour tout k de [[1,n]].
Raisonnons par récurrence. Si n = 1, A = (α) où α≠0. On a A = LU avec L = (1) et U = (α). Ainsi A vérifie (E1).
Supposons n ≥ 2 et que toute matrice carrée de taille n - 1 vérifiant (E1) vérifie (E2).
Notons α = A[1, 1], XA le vecteur-colonne des A[i,1] pour 2 ≤ i ≤ n, Y A le vecteur-colonne des A[1, j] pour 2 ≤ j ≤ n et Aʹ la matrice des A[i,j] pour 2 ≤ i,j ≤ n.
Ainsi A = 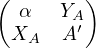 .
.
Par hypothèse α est non nul.
Conformément à la méthode du pivot partiel, on pose L1 = 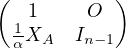 et il vient A = L1U1
où U1 =
et il vient A = L1U1
où U1 = 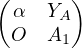 , avec A1 = Aʹ-
, avec A1 = Aʹ-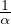 XAY A.
XAY A.
Soit k un entier compris entre 2 et n. On a :
L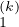 =
= 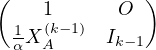 , U
, U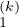 =
= 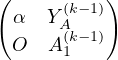 et A(k) =
et A(k) = 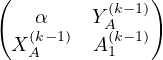 .
.
Ainsi det A(k) = αdetA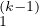 . Ainsi detA
. Ainsi detA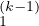 ≠0 pour 2 ≤ k ≤ n. La matrice A1 vérifie
l’hypothèse (E2 ).
≠0 pour 2 ≤ k ≤ n. La matrice A1 vérifie
l’hypothèse (E2 ).
Il existe donc une matrice L2 triangulaire inférieure inversible de taille n - 1, une matrice U2 triangulaire supérieure inversible de taille n - 1, telles que A2 = L2U2.
Posons L = L1 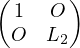 =
= 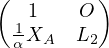 ; U =
; U = 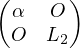 U1 =
U1 = 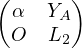 . Alors A = LU
où L est dans T
. Alors A = LU
où L est dans T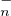 (C) et U est dans T
(C) et U est dans T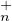 (C).
(C).
Donc si A vérifie (E2), alors A vérifie (E1).
19. L’application ϕk : A detA(k) est polynomiale vis-à-vis des coefficients de A ; elle
est donc continue. Il en résulte que l’ensemble Ωk des A tels que ϕk(A)≠0 est ouvert.
L’ensemble des matrices A vérifiant (E2) est donc l’ouvert Ω intersection des Ωk pour
1 ≤ k ≤ n.
detA(k) est polynomiale vis-à-vis des coefficients de A ; elle
est donc continue. Il en résulte que l’ensemble Ωk des A tels que ϕk(A)≠0 est ouvert.
L’ensemble des matrices A vérifiant (E2) est donc l’ouvert Ω intersection des Ωk pour
1 ≤ k ≤ n.
20. a) Notons S : A PτAPτ. Puisque τ •τ = id, on a aussi bien S(A) = Pτ-1APτ. Le calcul
fait en question 15. montre : S(A)[i,j] = A[n + 1 - i,n + 1 - j]. L’application S est involutive
comme τ.
PτAPτ. Puisque τ •τ = id, on a aussi bien S(A) = Pτ-1APτ. Le calcul
fait en question 15. montre : S(A)[i,j] = A[n + 1 - i,n + 1 - j]. L’application S est involutive
comme τ.
Puisque τ est strictement décroissante, si A est dans T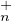 (C) (resp. T
(C) (resp. T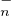 (C) ) alors A[i,j] = 0 pour
tous i > j (resp. i < j donc S(A)[i,j] = 0 pour tous i < j (resp. i > j).
(C) ) alors A[i,j] = 0 pour
tous i > j (resp. i < j donc S(A)[i,j] = 0 pour tous i < j (resp. i > j).
Ainsi S échange T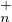 (C) et T
(C) et T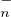 (C).
(C).
b) L’ensemble PτT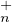 (C)PτT
(C)PτT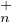 (C) n’est autre que l’ensemble T
(C) n’est autre que l’ensemble T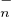 (C)T
(C)T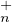 (C) qui lui-même est
l’ensemble des matrices vérifiant (E1) mais donc aussi (E2) d’après 18.. Ainsi cet ensemble est
l’ouvert noté Ω dans 19..
(C) qui lui-même est
l’ensemble des matrices vérifiant (E1) mais donc aussi (E2) d’après 18.. Ainsi cet ensemble est
l’ouvert noté Ω dans 19..
c) Soit A un élément quelconque de  n(C). L’ensemble Zk des λ tels que det(A(k) -λIk) = 0
est l’ensemble fini des valeurs propres de A(k). Si λ n’est pas dans la réunion Z des Zk alors
A - λIn est dans Ω.
n(C). L’ensemble Zk des λ tels que det(A(k) -λIk) = 0
est l’ensemble fini des valeurs propres de A(k). Si λ n’est pas dans la réunion Z des Zk alors
A - λIn est dans Ω.
Puisque Z est fini, il existe dans C \ Z une suite (λq)q N tendant vers 0. La suite de matrices
(A - λq In ) est une suite de Ω tendant vers A.
N tendant vers 0. La suite de matrices
(A - λq In ) est une suite de Ω tendant vers A.
L’ensemble Ω est dense dans  n(C) et, a fortiori, dans GLn(C).
n(C) et, a fortiori, dans GLn(C).
d) L’application A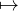 PτA est linéaire donc continue. Elle est involutive et envoie GLn(C) sur
GL(n, C ). C’est donc un homéomorphisme de GL(n, C).
PτA est linéaire donc continue. Elle est involutive et envoie GLn(C) sur
GL(n, C ). C’est donc un homéomorphisme de GL(n, C).
e) L’ensemble T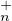 (C)PτT
(C)PτT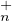 (C) est PτΩ. D’après la question précédente T
(C) est PτΩ. D’après la question précédente T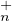 (C)PτT
(C)PτT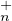 (C) est un
ouvert de GL n (C) et de plus cet ouvert est dense dans GLn(C).
(C) est un
ouvert de GL n (C) et de plus cet ouvert est dense dans GLn(C).
Le complémentaire de T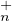 (C)PτT
(C)PτT (C) dans GL(n, C) est donc d’intérieur vide, et c’est la
réunion des T
(C) dans GL(n, C) est donc d’intérieur vide, et c’est la
réunion des T (C)PσT
(C)PσT (C) pour σ≠τ d’après le résultat admis à la fin de la partie
II.
(C) pour σ≠τ d’après le résultat admis à la fin de la partie
II.
Partie IV : décomposition de Bruhat et drapeaux
21. Soit B une base et g un automorphisme de E. Alors g ⋅B est une base qui est l’image par g de la base B.
On a id ⋅B = B.
Soit B = (e1 , … , en) ; soit g,h dans GL(E). Puisque g(h(ei)) = (gh)(ei) pour tout i, il vient : g ⋅ (h ⋅ B) = (gh) ⋅ B.
Ainsi (g, B)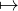 g ⋅ B est une action de groupes de GL(E) dans Δ.
g ⋅ B est une action de groupes de GL(E) dans Δ.
La propriété g ⋅ B = B revient à g = id. Tout stabilisateur est réduit à {id}. Donc, a fortiori, l’action étudiée est fidèle.
Soit B et Bʹ deux bases. Il existe un unique g de GL(E) telle que g ⋅B = Bʹ. L’action étudiée est transitive.
22. Soit D = (E0,E1,…,En) un drapeau total. Soit g un automorphisme de E. Alors (g(E0 ), g(E1 ), … ,g(En) est un drapeau total. En effet pour tout i, g(Ei) est un sous-espace vectoriel de dimension i et g(Ei-1) est inclus dans g(Ei) pour i ≥ 1. Donc g ⋅ D est un drapeau total.
On a bien sûr id ⋅D = D. Puisque g(h(Ei)) = (gh)(Ei) pour tout i, il vient : g ⋅ (h⋅D) = (gh) ⋅D.
Ainsi (g, D) g ⋅ D est une action de groupes de GL(E) dans
g ⋅ D est une action de groupes de GL(E) dans 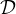 .
.
Soit B = (e1 , … , en) une base telle que δ(B) = D. Notons g ⋅ B = Bʹ = (eʹ1,…,eʹn), puis δ(Bʹ) = Dʹ = (Eʹ0,Eʹ1,…,Eʹn). Alors, pour tout i, g(Ei) = g(V ect(ei,…,ei)) = V ect(eʹ1,…,eʹi) = Eʹi. Ainsi g ⋅ δ(B) = δ(g ⋅ B). C’est la compatibilité demandée.
23. Soit D = (Ei) un drapeau et B = (ei) une base adaptée à D. La propriété g ⋅D = D revient
à : g(ei )  Ei pour tout i, soit : la matrice de g dans B est triangulaire supérieure, inversible
puisque g est un automorphisme.
Ei pour tout i, soit : la matrice de g dans B est triangulaire supérieure, inversible
puisque g est un automorphisme.
En particulier si B0 est la base canonique de Kn, le stabilisateur de δ(B0) dans GLn(K) est
T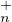 (K ).
(K ).
24. La relation M 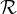 N revient à : M(T
N revient à : M(T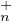 (K)) = N(T
(K)) = N(T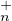 (K)) ; c’est dire que M et N
sont dans la même classe à gauche de GLn(K) modulo T
(K)) ; c’est dire que M et N
sont dans la même classe à gauche de GLn(K) modulo T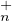 (K). C’est bien une relation
d’équivalence.
(K). C’est bien une relation
d’équivalence.
25. a) Soit M et N dans GLn(K). Supposons M = N. Alors MT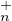 (K) = NT
(K) = NT (K). Donc
M ⋅ δ(B0 ) = (MN) ⋅ δ(B0). On peut donc poser φ(M) = M ⋅ δ(B0).
(K). Donc
M ⋅ δ(B0 ) = (MN) ⋅ δ(B0). On peut donc poser φ(M) = M ⋅ δ(B0).
b) Soit D un drapeau de Kn et B une base adaptée à D. Alors, M étant un élément de GLn(K) tel que M ⋅ B0 = B, on a M ⋅ δ(B0) = δ(B) = D. L’action de GLn(K) dans l’ensemble des drapeaux de K n est donc transitive et φ est surjective. Comme M ⋅ δ(B0) = N ⋅ δ(B0) revient à M= N , φ est bijective.
26. On a (XY ) ⋅ δ(B0) = X ⋅ (Y ⋅ δ(B0)) donc φ(XY ) = X ⋅ φ(Y ).
27. La question revient à trouver des matrices triangulaires supérieures inversibles T1 et T2
dans T (K ) et une permutation σ telles que Y = XT1PσT2. La décomposition de
Bruhat de X-1 Y donne une solution de ce problème dans laquelle T1 a une diagonale de
1.
(K ) et une permutation σ telles que Y = XT1PσT2. La décomposition de
Bruhat de X-1 Y donne une solution de ce problème dans laquelle T1 a une diagonale de
1.
Dans la question 16.b, on n’a pas besoin de supposer que les matrices U et Uʹ ont des diagonales de 1. On en déduit que toutes les solutions du problème donnent le même σ.
28. On vérifie que (A,(X,Y )) ,(AX,AY )) est une action de groupe de GLn(K) sur
(GL n (K )⁄T
,(AX,AY )) est une action de groupe de GLn(K) sur
(GL n (K )⁄T (K ))2. La question précédente montre que chaque orbite contient (In,Pσ) pour une
et une seule σ de 𝔖n. Le nombre d’orbites est donc n!.
(K ))2. La question précédente montre que chaque orbite contient (In,Pσ) pour une
et une seule σ de 𝔖n. Le nombre d’orbites est donc n!.
[Table des matières]

