[Table des matières]
Agrégation Interne de Mathématiques
Première Épreuve 2020
7046Décomposition de Bruhat.
Notations
- On désigne par N l’ensemble des entiers naturels, par N* l’ensemble des entiers naturels strictement positifs et par Z l’anneau des entiers relatifs.
- On désigne par R le corps des nombres réels, par C le corps des nombres complexes et par K l’un de ces deux corps lorsqu’on ne souhaite pas le préciser.
- Si m et n sont deux entiers relatifs, on pose [[m;n]] =
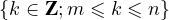 .
.
- Pour n entier naturel non nul, on note 𝔖n le groupe des permutations de [[1;n]].
- Si E est un K-espace vectoriel, on note L(E) l’ensemble des endomorphismes de E et GL(E) le groupe des endomorphismes inversibles.
- Pour une famille (u1,…,uk) de vecteurs de E, on note V ect(u1,…,uk) le sous-espace vectoriel de E engendré par cette famille.
- Soit n un entier naturel non nul. On note
 n(K) la K-algèbre des matrices (n,n) à
coefficients dans K et In la matrice identité dans
n(K) la K-algèbre des matrices (n,n) à
coefficients dans K et In la matrice identité dans  n(K).
n(K).
- On note GLn(K) le groupe multiplicatif des matrices inversibles, On(K) celui des matrices orthogonales et SOn(K) le groupe des matrices orthogonales de déterminant égal à 1.
- On note T
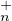 (K) le groupe multiplicatif des matrices triangulaires supérieures
inversibles et T
(K) le groupe multiplicatif des matrices triangulaires supérieures
inversibles et T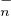 (K) le groupe multiplicatif des matrices triangulaires inférieures
inversibles.
(K) le groupe multiplicatif des matrices triangulaires inférieures
inversibles.
- Soit n un entier naturel non nul et A

 n(K).
n(K).
Pour i [[1;n]], on note Li la i-ème ligne de la matrice A. Pour j
[[1;n]], on note Li la i-ème ligne de la matrice A. Pour j  [[1;n]], on note
Cj la j-ème colonne de la matrice A.
[[1;n]], on note
Cj la j-ème colonne de la matrice A.
- Soit n un entier naturel non nul et (i,j)
 [[1;n]]2. On note Ei,j la matrice dont tous
les coefficients sont nuls sauf le coefficient situé à la i-ème ligne et à la j-ème colonne
qui vaut 1. Par exemple lorsque n = 2, on a :
[[1;n]]2. On note Ei,j la matrice dont tous
les coefficients sont nuls sauf le coefficient situé à la i-ème ligne et à la j-ème colonne
qui vaut 1. Par exemple lorsque n = 2, on a :
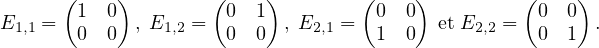
Rappels et compléments sur les actions de groupe (pour la partie IV)
- Soient (G, *) un groupe dont l’élément neutre est noté e et X un ensemble non vide. On
appelle action de G sur X toute application :
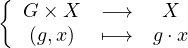 vérifiant les deux
propriétés suivantes :
vérifiant les deux
propriétés suivantes :
- 1.
- ∀x
 X, e ⋅ x = x
X, e ⋅ x = x
- 2.
- ∀g, h
 G, ∀x
G, ∀x  X, g ⋅ (h ⋅ x) = (g * h) ⋅ x
X, g ⋅ (h ⋅ x) = (g * h) ⋅ x
Lorsque l’on dispose d’une telle action, on dit que le groupe G agit sur l’ensemble X.
- Pour tout x
 X, on désigne par Ox l’orbite de x. Par définition :
X, on désigne par Ox l’orbite de x. Par définition :
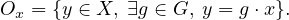
 , définie sur X par x
, définie sur X par x y ⇔ y
y ⇔ y  Ox, est une relation
d’équivalence sur X.
Ox, est une relation
d’équivalence sur X.
- Le stabilisateur d’un élément x de X est le sous-groupe de G défini par :
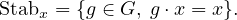
- On dit qu’une action est transitive (ou que le groupe G agit transitivement sur X) lorsque
l’action ne possède qu’une seule orbite. Autrement dit :
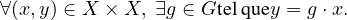
- On dira qu’une action est fidèle (ou que le groupe G agit fidèlement sur X) lorsque
l’intersection de tous les stabilisateurs est le sous-groupe {e} :
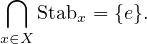
Partie I : drapeaux de sous-espaces vectoriels
Dans toute cette partie, E est un espace vectoriel de dimension finie n (n ≥ 1) sur K (on rappelle que K désigne indifféremment le corps des réels ou des complexes).
Soit p  N * . Une famille (Ei)0≤i≤p de sous-espaces vectoriels de E est appelée drapeau si elle
vérifie :
N * . Une famille (Ei)0≤i≤p de sous-espaces vectoriels de E est appelée drapeau si elle
vérifie :
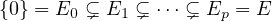
On dit qu’un drapeau (Ei)0≤i≤p est total lorsque p = n.
1. Soit (e1 , … , en ) une base de E.
On pose E0 = {0} et, ∀j  [[1;n]], Ej = V ect(e1,…,ej).
[[1;n]], Ej = V ect(e1,…,ej).
Montrer que (Ei )0≤i≤n est un drapeau total de E.
Étant donné un drapeau total (Ei)0≤i≤n, on dit qu’une base (e1,…,en) de E est adaptée à ce
drapeau si ∀j  [[1;n]], Ej = V ect(e1,…,ej).
[[1;n]], Ej = V ect(e1,…,ej).
2. Montrer que tout drapeau total admet une base adaptée.
3. Soit (Ei )0≤i≤n un drapeau total de E. Montrer que si E est un espace euclidien, alors il existe
une base orthonormée de E adaptée au drapeau.
Soit u  L(E). On dit qu’un drapeau (Ei)0≤i≤n est stable par u lorsque, pour tout i
L(E). On dit qu’un drapeau (Ei)0≤i≤n est stable par u lorsque, pour tout i  [[0;n]], le
sous-espace Ei est stable par u.
[[0;n]], le
sous-espace Ei est stable par u.
Dans la suite de cette partie, u désigne un endomorphisme de E.
4. On suppose dans cette question uniquement que u est diagonalisable. Montrer qu’il existe un drapeau total de E, stable par u.
5. On suppose dans cette question uniquement que u est nilpotent d’indice n, c’est-à-dire que u vérifie un = 0L(E) et un-1≠0L(E).
a) Soit k  [[1;n]] et x
[[1;n]] et x  E tel que un-1(x)≠0. Montrer que la famille (un-j(x))j
E tel que un-1(x)≠0. Montrer que la famille (un-j(x))j [[1;k]] est
libre.
[[1;k]] est
libre.
b) Montrer que (Kerui)0≤i≤n est un drapeau total de E, stable par u. Construire une base adaptée à ce drapeau.
6. Montrer que u est trigonalisable si et seulement si E admet un drapeau total stable par u.
7. Montrer à l’aide des questions précédentes que si E est euclidien et que u est trigonalisable,
alors il existe une base orthonormée de E dans laquelle la matrice de u est triangulaire
supérieure.
Partie II : des groupes quotients
Dans cette partie, on désigne par G un groupe dont la loi est notée multiplicativement et H un sous-groupe de G. On note 1G l’élément neutre de G.
On rappelle que si g  G, on désigne par gH l’ensemble appelé classe à gauche :
G, on désigne par gH l’ensemble appelé classe à gauche :
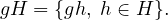
De manière analogue, on appelle l’ensemble Hg une classe à droite.
On rappelle que la relation binaire définie par : g1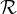 g2 ⇔ g2
g2 ⇔ g2  g1H est une relation d’équivalence,
dont les classes sont les ensembles du type gH et que l’on désigne par G⁄H l’ensemble quotient
pour cette relation.
g1H est une relation d’équivalence,
dont les classes sont les ensembles du type gH et que l’on désigne par G⁄H l’ensemble quotient
pour cette relation.
On dit que le sous-groupe H est distingué dans G lorsque : ∀g  G, gH = Hg. On note dans ce
cas H ⊲ G. On remarquera que H ⊲ G ⇔∀g
G, gH = Hg. On note dans ce
cas H ⊲ G. On remarquera que H ⊲ G ⇔∀g  G, g-1Hg ⊂ H.
G, g-1Hg ⊂ H.
8. Soit H ⊲ G.
a) Montrer que G⁄H peut être muni d’une structure de groupe en considérant la loi de
composition ⋆ définie par (g1H) ⋆ (g2H) = (g1g2)H.
On expliquera pourquoi on a bien défini ainsi une loi de composition interne sur G⁄H.
b) Montrer que l’application π : G → G⁄H définie pour tout g  G par π(g) = gH est un
morphisme de groupe surjectif.
G par π(g) = gH est un
morphisme de groupe surjectif.
9. On désigne dans cette question par TU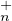 (K) le groupe des matrices triangulaires supérieures
dont tous les coefficients diagonaux valent 1.
(K) le groupe des matrices triangulaires supérieures
dont tous les coefficients diagonaux valent 1.
a) Montrer que TU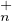 (K) ⊲ T
(K) ⊲ T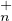 (K).
(K).
b) A-t-on TU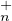 (K) ⊲ GLn(K) ?
(K) ⊲ GLn(K) ?
10. Soit H un sous-groupe quelconque de G. On suppose que G⁄H est un ensemble fini à deux éléments. Montrer que H ⊲ G.
11. Dans cette question uniquement, on pose A = 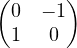 et B =
et B = 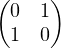 .
.
On désigne par
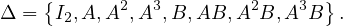
a) Vérifier que A3B = BA, et montrer que Δ est un sous-groupe de GL2(R).
b) On définit Γ =< A > le sous-groupe de Δ engendré par A et R =< B > le sous-groupe de Δ engendré par B. Montrer que Δ⁄Γ est un groupe, isomorphe à R.
c) Existe-t-il un isomorphisme entre les groupes Δ et Γ × R ?
Soient H et K deux sous-groupes quelconques de G. Pour tout g  G on appelle double classe de g
relative aux sous-groupes H et K l’ensemble :
G on appelle double classe de g
relative aux sous-groupes H et K l’ensemble :
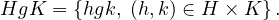
Dans la suite, H et K étant fixés, on parlera simplement de ≪ la double classe d’un élément de G ≫ .
12. a) Montrer qu’une double classe est une réunion de classes à gauche, et aussi une réunion de classes à droite.
b) Montrer que les doubles classes relatives aux sous-groupes H et K constituent une partition
de G.
Partie III : décomposition de Bruhat et matrices
Dans cette partie, E est un K-espace vectoriel de dimension n (n  N*).
N*).
On munit E d’une base  = (ε1,…,εn).
= (ε1,…,εn).
13. Pour σ  𝔖n, soit uσ l’endomorphisme de E défini par l’égalité :
𝔖n, soit uσ l’endomorphisme de E défini par l’égalité :
![∀i ∈ [[1;n]], uσ(εi) = εσ(i)](/numeros/RMS130-4/RMS130-4316x.png)
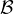 . Une telle matrice Pσ est appelée matrice de permutation.
. Une telle matrice Pσ est appelée matrice de permutation.
a) Dans cette question uniquement, σ est le n-cycle (1,2,…,n). Expliciter la matrice Pσ .
b) Soit σ  𝔖n. On note σ = c1
𝔖n. On note σ = c1 ck une décomposition de σ en cycles de supports disjoints, où
k
ck une décomposition de σ en cycles de supports disjoints, où
k  N * . Exprimer la matrice Pσ en fonction des matrices Pcj pour j
N * . Exprimer la matrice Pσ en fonction des matrices Pcj pour j  [[1;k]].
[[1;k]].
c) Montrer que Pσ  On(R).
On(R).
d) À quelle condition sur σ la matrice Pσ appartient-elle à SOn(R) ?
14. Pour λ  K et (i,j)
K et (i,j)  [[1;n]]2 , on note Ti,j(λ) la matrice In + λEi,j.
[[1;n]]2 , on note Ti,j(λ) la matrice In + λEi,j.
Pour λ  K et i
K et i  [[1;n]], on note Di(λ) la matrice In + (λ - 1)Ei,i.
[[1;n]], on note Di(λ) la matrice In + (λ - 1)Ei,i.
Soit A 
 n (K ).
n (K ).
a) Montrer que la matrice Ti,j(λ)A est obtenue à partir de A en effectuant l’opération élémentaire Li ← Li + λLj.
b) De manière analogue, donner les opérations élémentaires à effectuer pour obtenir les matrices Di (λ)A, ATi,j (λ) et ADi(λ).
c) Donner les opérations élémentaires à effectuer pour obtenir les matrices Pi,jA et
APi,j , où Pi,j désigne la matrice Pσ lorsque σ est la transposition (i,j). Expliquer sans
démonstration comment obtenir PσA et APσ à partir de A, lorsque σ  𝔖n est une permutation
quelconque.
𝔖n est une permutation
quelconque.
15. Soient U et V deux matrices triangulaires supérieures inversibles et soient σ et σʹ deux
permutations.
On suppose que P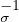 UPσʹ = V . Montrer que σ = σʹ. Indication : On pourra considérer le
coefficient d’indice (σ(j),j) de PσV , où j
UPσʹ = V . Montrer que σ = σʹ. Indication : On pourra considérer le
coefficient d’indice (σ(j),j) de PσV , où j  [[1;n]].
[[1;n]].
16. Soit A  GLn(K) une matrice inversible.
GLn(K) une matrice inversible.
a) Montrer qu’il existe une matrice triangulaire supérieure U ne comportant que des 1 sur la diagonale, une matrice triangulaire supérieure V et une matrice de permutation Pσ telles que A = UPσ V et que cette écriture peut être obtenue à l’aide d’opérations élémentaires sur les lignes et les colonnes de la matrice A. On appelle cette écriture décomposition de Bruhat de la matrice A.
b) Montrer que la matrice Pσ de la question précédente est uniquement déterminée par
A.
Le résultat de la question 16. permet donc d’affirmer que GLn(K) ⊂⋃
σ 𝔖nT
𝔖nT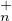 (K)PσT
(K)PσT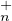 (K).
(K).
Nous admettrons par la suite que cette inclusion est une égalité.
17. Déterminer la décomposition de Bruhat d’une matrice A = 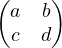
 SL2(K) i.e. telle que
ad - bc = 1.
SL2(K) i.e. telle que
ad - bc = 1.
Jusqu’à la fin de cette partie, on se place dans le cas où K = C et on munit  n(C) d’une norme
quelconque ∥⋅ ∥.
n(C) d’une norme
quelconque ∥⋅ ∥.
Les mineurs principaux d’une matrice A = (ai,j)(i,j) [[1;n]]2
[[1;n]]2 
 n(C) sont les déterminants des
matrices extraites (ai,j)(i,j)
n(C) sont les déterminants des
matrices extraites (ai,j)(i,j) [[1;k]]2 pour tout k
[[1;k]]2 pour tout k  [[1;n]], ces matrices étant obtenues en ne
conservant que les k premières lignes et k premières colonnes de la matrice A.
[[1;n]], ces matrices étant obtenues en ne
conservant que les k premières lignes et k premières colonnes de la matrice A.
18. On considère les deux propositions ci-dessous, où A 
 n(C) :
n(C) :
- : la matrice A s’écrit comme produit d’un élément de T
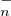 (C) et d’un élément de
T
(C) et d’un élément de
T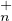 (C ),
(C ),
- : les mineurs principaux de A sont tous non nuls.
a) Montrer que si A satisfait la propriété (E1) ou la propriété (E2) alors A  GLn(C).
GLn(C).
b) À l’aide d’une décomposition par blocs, montrer que (E1)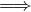 (E2).
(E2).
c) En procédant par récurrence, montrer que (E2)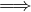 (E1).
(E1).
19. Montrer que l’ensemble des matrices qui vérifient la condition (E2) est un ouvert de GLn(C).
Indication : on pourra considérer pour k  [[1;n]] l’application ϕk de
[[1;n]] l’application ϕk de  n(C) dans C qui à une
matrice A, associe son mineur principal d’ordre k.
n(C) dans C qui à une
matrice A, associe son mineur principal d’ordre k.
20. Soit τ  𝔖n définie, pour tout k
𝔖n définie, pour tout k  [[1;n]], par : τ(k) = n - k + 1.
[[1;n]], par : τ(k) = n - k + 1.
a) Montrer que : PτT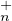 (C)Pτ = T
(C)Pτ = T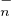 (C), où PτT
(C), où PτT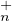 (C)Pτ désigne l’ensemble
(C)Pτ désigne l’ensemble
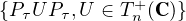 .
.
b) Montrer que PτT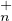 (C)PτT
(C)PτT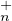 (C) =
(C) = 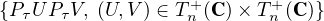 est un ouvert
de GL n (C ).
est un ouvert
de GL n (C ).
c) Montrer que PτT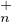 (C)PτT
(C)PτT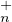 (C) est dense dans GLn(C).
(C) est dense dans GLn(C).
d) Montrer que l’application : 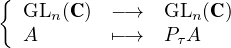 réalise un homéomorphisme.
réalise un homéomorphisme.
e) En déduire que T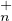 (C)PτT
(C)PτT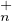 (C) est un ouvert dense de GLn(C). Que peut-on affirmer sur la
topologie de l’ensemble ⋃
(C) est un ouvert dense de GLn(C). Que peut-on affirmer sur la
topologie de l’ensemble ⋃
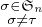 T
T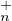 (C)PσT
(C)PσT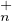 (C) ?
(C) ?
Partie IV : décomposition de Bruhat et drapeaux
Soit E un K -espace vectoriel de dimension n  N*.
N*.
On note 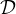 l’ensemble des drapeaux totaux de E et Δ l’ensemble des bases de E.
l’ensemble des drapeaux totaux de E et Δ l’ensemble des bases de E.
Dans cette partie, on désigne par δ l’application de Δ à valeurs dans 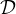 qui, à une base
B = (e1 , … , en ), associe le drapeau total
qui, à une base
B = (e1 , … , en ), associe le drapeau total 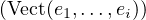 i
i [[1;n]].
[[1;n]].
21. Montrer que le groupe linéaire GL(E) agit fidèlement et transitivement sur l’ensemble Δ par :
![g⋅(ei)i∈[[1;n]] = (g(ei))i∈[[1;n]].](/numeros/RMS130-4/RMS130-4342x.png)
22. Montrer que GL(E) agit transitivement sur l’ensemble 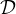 par :
par :
![g ⋅(Ei)i∈[[1;n]] = (g(Ei))i∈[[1;n]]](/numeros/RMS130-4/RMS130-4343x.png)
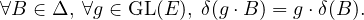
Dans la suite de la partie, via le choix d’une base B0 = (ε1,…,εn), on identifie E à Kn et le groupe linéaire GL (E) à l’ensemble GLn(K) des matrices inversibles.
23. Montrer que le stabilisateur de δ(B0) s’identifie au sous-groupe T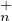 (K) des matrices
triangulaires supérieures inversibles.
(K) des matrices
triangulaires supérieures inversibles.
24. On définit la relation 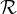 sur GLn(K) par : M
sur GLn(K) par : M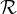 N si et seulement si M-1N
N si et seulement si M-1N  T
T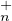 (K), pour
M, N
(K), pour
M, N  GL n (K ). Montrer que
GL n (K ). Montrer que 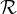 est une relation d’équivalence.
est une relation d’équivalence.
Pour M  GL n (K), on note M la classe de M dans l’ensemble quotient GLn(K)⁄T
GL n (K), on note M la classe de M dans l’ensemble quotient GLn(K)⁄T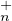 (K).
(K).
25. On considère l’application φ suivante :
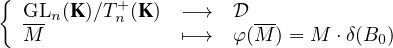
a) Montrer que φ est bien définie.
b) Montrer que φ est une bijection de GLn(K)⁄T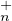 (K) sur
(K) sur 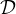 .
.
26. Montrer que pour tout X et Y de GLn(K), on a φ(XY ) = X ⋅ φ(Y ).
On considère l’action du groupe GLn(K) sur l’ensemble GLn(K)⁄T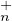 (K) ×GLn(K)⁄T
(K) ×GLn(K)⁄T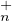 (K)
définie par A ⋅ (X,Y ) = (AX,AY ).
(K)
définie par A ⋅ (X,Y ) = (AX,AY ).
27. Soient X et Y dans GLn(K). À l’aide de la décomposition de Bruhat, montrer qu’il existe
σ  𝔖n et T1
𝔖n et T1  T
T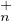 (K) tel que (X,Y ) = XT1 ⋅ (In,Pσ), et que σ est unique.
(K) tel que (X,Y ) = XT1 ⋅ (In,Pσ), et que σ est unique.
28. En déduire le nombre d’orbites dans l’action de GLn(K) sur
GLn(K )⁄T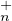 (K ) × GLn(K)⁄T
(K ) × GLn(K)⁄T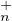 (K).
(K).
——————-FIN DU SUJET ——————-
[Table des matières]

