333. On munit Rn de la norme euclidienne canonique, notée ∥∥ et on considère ρ  R+*, v
une application de Rn dans lui-même ρ-lipschitzienne pour ∥∥, X une application de classe C1
telle que ∀t
R+*, v
une application de Rn dans lui-même ρ-lipschitzienne pour ∥∥, X une application de classe C1
telle que ∀t  [0, 1],Xʹ(t) = v(X(t)). Soit N
[0, 1],Xʹ(t) = v(X(t)). Soit N  N*. Pour k
N*. Pour k  {0,…,N}, on pose X
{0,…,N}, on pose X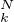 = X
= X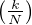 et on définit par récurrence ξ
et on définit par récurrence ξ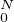 = X(0) et si k ≥ 1, ξ
= X(0) et si k ≥ 1, ξ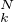 = ξ
= ξ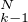 +
+ 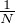 v(ξ
v(ξ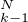 ). On note pour
k
). On note pour
k  {0, … , N}, ε
{0, … , N}, ε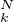 = ∥ξ
= ∥ξ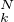 - X
- X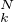 ∥ et εN = max{ε
∥ et εN = max{ε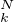 ;k
;k  {0,…,N}}. Montrer que εN → 0
quand N → +∞.
{0,…,N}}. Montrer que εN → 0
quand N → +∞.
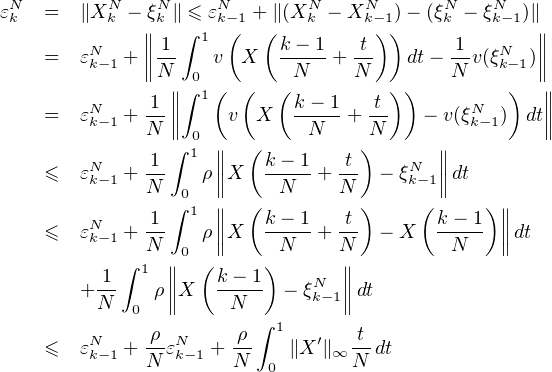
soit
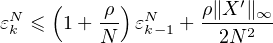
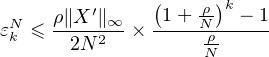
![ʹ [( )N ] ρ ʹ
εNk ≤ ρ∥X-∥∞- × 1+ -ρ - 1 ≤ (e----1)∥X--∥∞--
2N N 2N](/numeros/RMS130-3/RMS130-32085x.png)
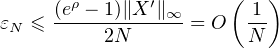
 R+*, v
une application de Rn dans lui-même ρ-lipschitzienne pour ∥∥, X une application de classe C1
telle que ∀t
R+*, v
une application de Rn dans lui-même ρ-lipschitzienne pour ∥∥, X une application de classe C1
telle que ∀t  [0, 1],Xʹ(t) = v(X(t)). Soit N
[0, 1],Xʹ(t) = v(X(t)). Soit N  N*. Pour k
N*. Pour k  {0,…,N}, on pose X
{0,…,N}, on pose X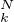 = X
= X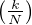 et on définit par récurrence ξ
et on définit par récurrence ξ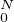 = X(0) et si k ≥ 1, ξ
= X(0) et si k ≥ 1, ξ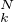 = ξ
= ξ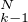 +
+ 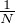 v(ξ
v(ξ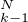 ). On note pour
k
). On note pour
k  {0, … , N}, ε
{0, … , N}, ε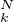 = ∥ξ
= ∥ξ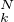 - X
- X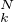 ∥ et εN = max{ε
∥ et εN = max{ε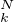 ;k
;k  {0,…,N}}. Montrer que εN → 0
quand N → +∞.
{0,…,N}}. Montrer que εN → 0
quand N → +∞.
Pour k = 1, … , N
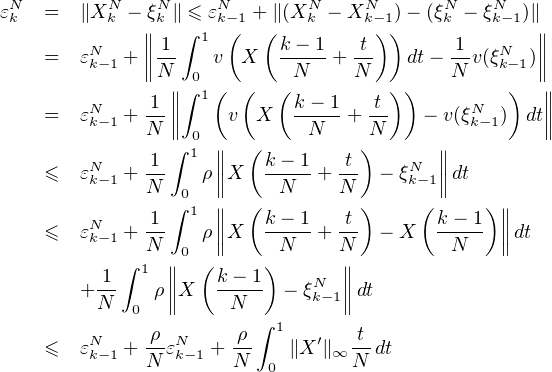
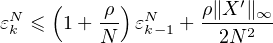
On peut supposer ρ > 0 et on a, par récurrence immédiate sur k en tenant compte de
ε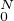 = 0,
= 0,
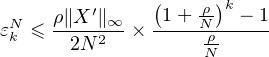
soit
![ʹ [( )N ] ρ ʹ
εNk ≤ ρ∥X-∥∞- × 1+ -ρ - 1 ≤ (e----1)∥X--∥∞--
2N N 2N](/numeros/RMS130-3/RMS130-32085x.png)
Ainsi
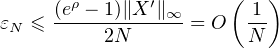
ce qui montre que εN tend vers 0 quand N tend vers + ∞.

