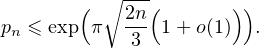![]- 1,1[](/numeros/RMS130-3/RMS130-32018x.png) et n
et n  N*, on note Pn(x) =
N*, on note Pn(x) = 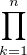
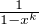 ⋅
⋅
a) Montrer que, si x 
![]- 1,1[](/numeros/RMS130-3/RMS130-32021x.png) , (Pn(x))n≥1 converge. On note P(x) sa limite.
, (Pn(x))n≥1 converge. On note P(x) sa limite.
b) Montrer que, pour x 
![]- 1,1[](/numeros/RMS130-3/RMS130-32022x.png) , P(x) = 1 +
, P(x) = 1 + 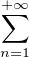 pnxn où, pour n
pnxn où, pour n  N*, pn est le
nombre de façons d’écrire n comme somme d’éléments de N* sans tenir compte de
l’ordre.
N*, pn est le
nombre de façons d’écrire n comme somme d’éléments de N* sans tenir compte de
l’ordre.
c) Montrer que, lorsque x → 1-, P(x) = exp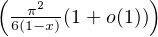 .
.
d) Montrer que, lorsque n → +∞, pn ≤ exp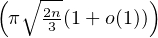 .
.
a) Soit x 
![]-1,1[](/numeros/RMS130-3/RMS130-32026x.png) . Comme xk < 1 pour tout k
. Comme xk < 1 pour tout k  N*, on a
N*, on a
![[ n ]
* ∑ ( k )
∀n ∈ N ,Pn(x) = exp - ln(1- x ) .
k=1](/numeros/RMS130-3/RMS130-32027x.png)
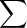 xn converge absolument, on en déduit
que
xn converge absolument, on en déduit
que 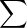 (-ln(1 - xn)) converge. On conclut que (Pn(x))n converge vers un élément de R
(-ln(1 - xn)) converge. On conclut que (Pn(x))n converge vers un élément de R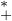 . En
vue de la suite, on notera que
. En
vue de la suite, on notera que
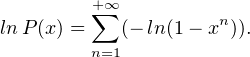 | (1) |
b) Précisons la notation pn. Fixons n  N (éventuellement nul). On dit qu’une suite (ak)k≥1
d’éléments de N est une partition de n lorsque n =
N (éventuellement nul). On dit qu’une suite (ak)k≥1
d’éléments de N est une partition de n lorsque n = 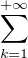 kak. Notons qu’une telle suite a doit vérifier
ak = 0 pour tout k ≥ n + 1, et ak ≤ n pour tout k
kak. Notons qu’une telle suite a doit vérifier
ak = 0 pour tout k ≥ n + 1, et ak ≤ n pour tout k  [ [1,n]]. L’ensemble
[ [1,n]]. L’ensemble  n des partitions de n est
donc fini ; on note pn son cardinal. Plus particulièrement, notons
n des partitions de n est
donc fini ; on note pn son cardinal. Plus particulièrement, notons 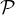 n,N, pour N
n,N, pour N  N*, l’ensemble
des partitions a de n telles que ak = 0 pour tout k > N ; posons pn,N := |
N*, l’ensemble
des partitions a de n telles que ak = 0 pour tout k > N ; posons pn,N := |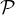 n,N|. On
observe que pn,N = pn pour tout N ≥ n, que pn,1 = 1, et que la suite (pn,N)N≥0 est
croissante.
n,N|. On
observe que pn,N = pn pour tout N ≥ n, que pn,1 = 1, et que la suite (pn,N)N≥0 est
croissante.
Fixons x 
![]-1,1[](/numeros/RMS130-3/RMS130-32033x.png) . Par récurrence sur N
. Par récurrence sur N  N*, on montre la propriété
N*, on montre la propriété
HN : ≪ 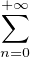 pn,Nxn = PN(x) avec convergence absolue ≫.
pn,Nxn = PN(x) avec convergence absolue ≫.
L’assertion H0 est triviale, tandis que H1 découle du développement P1(x) = 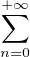 xn. Soit N ≥ 2
tel que HN-1 soit vraie. Alors,
xn. Soit N ≥ 2
tel que HN-1 soit vraie. Alors,
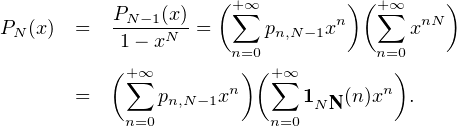
 dnxn avec convergence absolue, où, pour tout n
dnxn avec convergence absolue, où, pour tout n  N,
N,
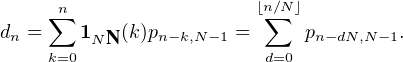
Soit n  N . Pour tout d
N . Pour tout d  [ [0,⌊n⁄N⌋]], on met en bijection l’ensemble des éléments de
[ [0,⌊n⁄N⌋]], on met en bijection l’ensemble des éléments de 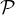 n,N dont le
N-ième terme est d avec
n,N dont le
N-ième terme est d avec 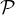 n-Nd,N-1 en associant à a la suite (a1,…,aN-1,0,0,…). En
partitionnant
n-Nd,N-1 en associant à a la suite (a1,…,aN-1,0,0,…). En
partitionnant  n,N selon le N-ième terme, il vient dn = pn,N. La propriété HN est donc
établie.
n,N selon le N-ième terme, il vient dn = pn,N. La propriété HN est donc
établie.
Convenons que P-1(x) = 0 et pn,-1 = 0 pour tout n  N. Nous avons donc
N. Nous avons donc
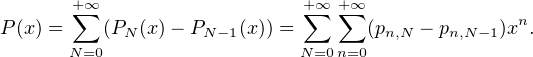
 N2 est sommable puisque le raisonnement précédent,
appliqué à |x| au lieu de x, donne
N2 est sommable puisque le raisonnement précédent,
appliqué à |x| au lieu de x, donne
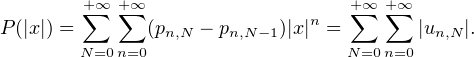
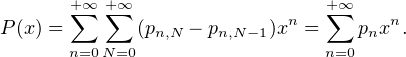
c) Fixons x 
![]0,1[](/numeros/RMS130-3/RMS130-32042x.png) . Pour tout n
. Pour tout n  N*, on a |xn| < 1, donc, par développement en série entière du
logarithme, l’égalité () donne
N*, on a |xn| < 1, donc, par développement en série entière du
logarithme, l’égalité () donne
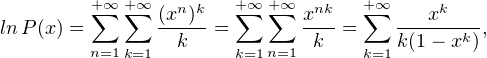
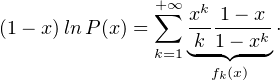
 N * . Alors,
N * . Alors,
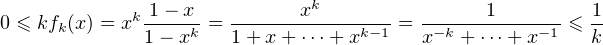 | (2) |
car x-i ≥ 1 pour tout i  N. L’égalité dans () montre que fk tend vers
N. L’égalité dans () montre que fk tend vers 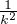 en 1-. En
outre,
en 1-. En
outre,
![* -1
∀k ∈ N ,∀x ∈ ]0,1[,|fk(x)| ≤ k2 ⋅](/numeros/RMS130-3/RMS130-32047x.png)
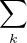 fk sur
fk sur ![]0,1[](/numeros/RMS130-3/RMS130-32049x.png) , donc
, donc
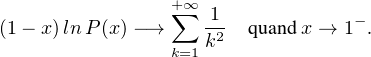
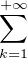
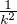 =
= 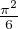 (ce résultat ne figure pas au programme et il est douteux que
l’examinateur en attendît une démonstration). Ainsi, quand x tend vers 1-, on trouve
(1 - x) ln P(x) =
(ce résultat ne figure pas au programme et il est douteux que
l’examinateur en attendît une démonstration). Ainsi, quand x tend vers 1-, on trouve
(1 - x) ln P(x) = 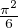 + o(1) puis
+ o(1) puis
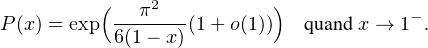
d) Posons λ := 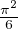 ⋅ Nous remarquons que l’inégalité () donne directement la majoration :
⋅ Nous remarquons que l’inégalité () donne directement la majoration :
![∀x ∈ ]0,1[,P(x) ≤ exp(λ(1- x)-1).](/numeros/RMS130-3/RMS130-32057x.png)

![]0,1[](/numeros/RMS130-3/RMS130-32058x.png) quelconque. Comme (pk)k est à terme général positif, le résultat de b) donne en
particulier pn xn ≤ P(x), d’où
quelconque. Comme (pk)k est à terme général positif, le résultat de b) donne en
particulier pn xn ≤ P(x), d’où
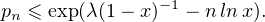 | (3) |
Une étude des variations de u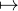 λu-1 -nln(1 -u) sur
λu-1 -nln(1 -u) sur ![]0,1[](/numeros/RMS130-3/RMS130-32061x.png) montre que, lorsque n est grand, son
minimum est atteint en un point proche de
montre que, lorsque n est grand, son
minimum est atteint en un point proche de 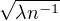 . Cela invite à prendre x := 1 -
. Cela invite à prendre x := 1 -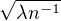 dans (), à condition que n > λ (condition que nous supposerons désormais remplie). Il
vient
dans (), à condition que n > λ (condition que nous supposerons désormais remplie). Il
vient
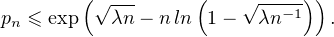
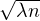 - nln(1 -
- nln(1 -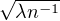 ) = 2
) = 2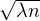 + o(
+ o(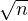 ) quand n → +∞. Il vient donc
) quand n → +∞. Il vient donc