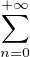CN*
avec a1≠0. On suppose que le rayon de convergence de
CN*
avec a1≠0. On suppose que le rayon de convergence de
 anzn est supérieur ou égal à R. On cherche à construire (bn)n≥1
anzn est supérieur ou égal à R. On cherche à construire (bn)n≥1  CN*
telle que
g : z
CN*
telle que
g : z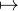
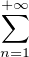 bnzn ait un rayon de convergence > 0 et (f • g)(z) = z au voisinage de
0.
bnzn ait un rayon de convergence > 0 et (f • g)(z) = z au voisinage de
0.
a) Montrer qu’il existe une unique suite (bn)n N*
N*  CN*
telle que : (*) :
CN*
telle que : (*) :
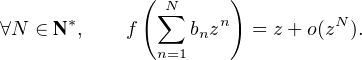
b) Soit (An )n≥1  (R+)N*
telle que A1 = |a1| et, pour n
(R+)N*
telle que A1 = |a1| et, pour n  N*, An ≥|an|. On suppose que le
rayon de convergence de
N*, An ≥|an|. On suppose que le
rayon de convergence de 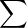 Anzn est strictement positif. On définit, au voisinage de 0, la
fonction F : z
Anzn est strictement positif. On définit, au voisinage de 0, la
fonction F : z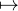 A1z -
A1z -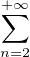 Anzn. On considère la suite (Bn)n≥1
Anzn. On considère la suite (Bn)n≥1  CN*
telle que,
pour tout N
CN*
telle que,
pour tout N  N*, F
N*, F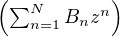 = z + o(zN). Montrer que, pour tout n
= z + o(zN). Montrer que, pour tout n  N*,
Bn ≥ |bn |.
N*,
Bn ≥ |bn |.
c) Soit r 
![]0,R[](/numeros/RMS130-3/RMS130-31974x.png) et M =
et M = 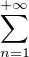 |an|rn. Pour N
|an|rn. Pour N  N*, on pose AN =
N*, on pose AN = 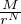 . Montrer que les rayons
de convergence de
. Montrer que les rayons
de convergence de 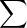 Bnzn et de
Bnzn et de 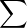 bnzn sont strictement positifs.
bnzn sont strictement positifs.
d) Conclure.
Théorème d’inversion local à droite d’une fonction développable en série entière.
Nous utiliserons deux résultats classiques
Proposition 1.Soient u  CN et v
CN et v  CN*
. On suppose que les fonctions
CN*
. On suppose que les fonctions
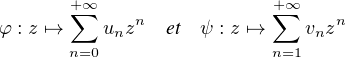
 φ • ψ(z) est bien définie et est la somme d’une série entière.
φ • ψ(z) est bien définie et est la somme d’une série entière.
Démonstration. On sait que ∀x  ] - 1,1[,
] - 1,1[, 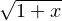 =
= 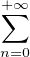
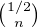 xn. Donc le rayon de convergence
de la série entière
xn. Donc le rayon de convergence
de la série entière 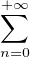
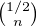 zn est supérieur ou égal à 1 et β est bien définie. Comme β2 est la
somme d’une série entière et que ∀x
zn est supérieur ou égal à 1 et β est bien définie. Comme β2 est la
somme d’une série entière et que ∀x  ] - 1,1[, β2(x) = 1 + x, on a, par unicité du développement
en série entière ∀z
] - 1,1[, β2(x) = 1 + x, on a, par unicité du développement
en série entière ∀z  B(0,1), β(z)2 = 1 + z. __
B(0,1), β(z)2 = 1 + z. __
a) Unicité. Soit b  CN*
qui convient. Pour N
CN*
qui convient. Pour N  N*, z
N*, z f
f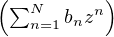 est développable en
série entière autour de 0 et on a, en examinant le coefficient de zN
est développable en
série entière autour de 0 et on a, en examinant le coefficient de zN
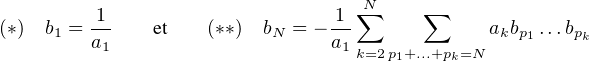
Les formules (*) et (**) caractérisent la suite (bn) qui est donc unique.
Existence. Les formules (*) et (**) définissent une suite (bn) qui est manifestement solution.
b) On a B1 = 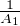 et, pour N ≥ 2,
et, pour N ≥ 2,
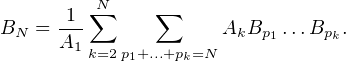
c) On a bien |AN |≥|aN| pour tout N  N* et, pour |Z| < r,
N* et, pour |Z| < r,
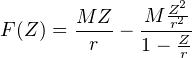
Pour z  C tel que |z| < r, on considère l’équation (
C tel que |z| < r, on considère l’équation (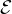 z) d’inconnue Z
z) d’inconnue Z  C \{r},
C \{r},
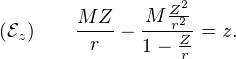
On vérifie immédiatement que si 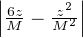 < 1,
< 1,
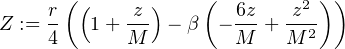
est une solution de (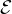 z).
z).
On choisit alors r1 > 0 tel que r1 ≤ r et |z| < r1 ⇒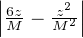 < 1 et on définit à bon
droit
< 1 et on définit à bon
droit
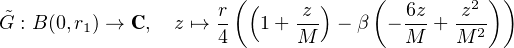
Selon la proposition 1, il existe r2  ]0,r1] tel que
]0,r1] tel que 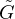 est développable en série entière sur B(0,r2).
Comme
est développable en série entière sur B(0,r2).
Comme 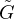 (0) = 0, on peut poser, pour |z| < r2,
(0) = 0, on peut poser, pour |z| < r2, 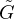 (z) =
(z) = 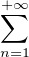
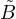 nzn.
nzn.
Pour |z| < r2 , on a donc F •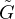 (z) = z. Si N
(z) = z. Si N  N*, on a ainsi
N*, on a ainsi
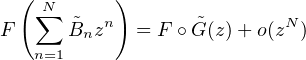
d’où 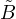 N = BN , d’où l’on déduit que le rayon de convergence de la série entière
N = BN , d’où l’on déduit que le rayon de convergence de la série entière 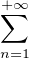 Bnzn est égal
à celui de la série entière
Bnzn est égal
à celui de la série entière 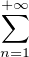
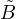 nzn, donc est strictement positif et que par conséquent celui de la
série entière
nzn, donc est strictement positif et que par conséquent celui de la
série entière 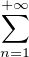 bnzn est également strictement positif.
bnzn est également strictement positif.
d) Soient rʹ le rayon de convergence de la série entière 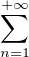 bnzn et g : B(0,rʹ) → C, z
bnzn et g : B(0,rʹ) → C, z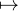
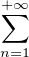 bnzn.
Selon la proposition 1, on dispose de rʹʹ > 0 tel que f • g est définie et développable en série
entière sur B(0, rʹʹ).
bnzn.
Selon la proposition 1, on dispose de rʹʹ > 0 tel que f • g est définie et développable en série
entière sur B(0, rʹʹ).
Pour N  N * , on a, lorsque z tend vers 0,
N * , on a, lorsque z tend vers 0,
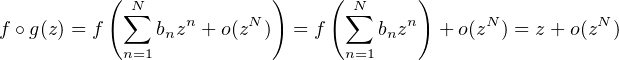
Donc le développement en série entière de z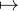 f • g(z) est z
f • g(z) est z z et ainsi, ∀z
z et ainsi, ∀z  B(0,rʹʹ),
f • g(z) = z.
B(0,rʹʹ),
f • g(z) = z.