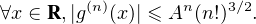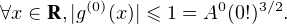R*,g(x) = exp(-x-2).
Montrer que g est de classe C∞ sur R mais n’est pas développable en série entière en
0.
R*,g(x) = exp(-x-2).
Montrer que g est de classe C∞ sur R mais n’est pas développable en série entière en
0.
b) Soit f : R → R de classe C∞. Montrer que f est développable en série entière en 0 si et
seulement s’il existe a > 0, M > 0 et A > 0 tels que ∀n  N,∀x
N,∀x  [-a,a],|f(n)(x)|≤ MAnn!.
[-a,a],|f(n)(x)|≤ MAnn!.
c) Établir l’existence de A > 0 tel que ∀n  N,∀x
N,∀x  R,|g(n)(x)|≤ (n!)3⁄2An.
R,|g(n)(x)|≤ (n!)3⁄2An.
a) On définit une suite (Qn)n N de polynômes par récurrence en posant Q0 = 1 et
Qn+1 = -X2 Qn ʹ + 2X3Qn pour tout n
N de polynômes par récurrence en posant Q0 = 1 et
Qn+1 = -X2 Qn ʹ + 2X3Qn pour tout n  N. À partir de la formule de dérivation d’un produit et
d’une composée, une récurrence facile montre que, pour tout n
N. À partir de la formule de dérivation d’un produit et
d’une composée, une récurrence facile montre que, pour tout n  N, la restriction h de g à R* est n
fois dérivable et de dérivée n-ième x
N, la restriction h de g à R* est n
fois dérivable et de dérivée n-ième x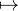 Qn(x-1)e-x-2
. Par croissances comparées
(x-1 )k e-x-2
tend vers 0 quand x tend vers 0, pour tout k
Qn(x-1)e-x-2
. Par croissances comparées
(x-1 )k e-x-2
tend vers 0 quand x tend vers 0, pour tout k  N, donc par combinaison
linéaire h(n) a pour limite 0 en 0 pour tout n
N, donc par combinaison
linéaire h(n) a pour limite 0 en 0 pour tout n  N. Ainsi, h admet un unique prolongement
N. Ainsi, h admet un unique prolongement
 : R → R de classe C∞. En particulier
: R → R de classe C∞. En particulier 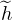 (0) = lim0h = 0, donc
(0) = lim0h = 0, donc 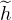 = g, et le résultat voulu
est démontré. En outre, pour tout n
= g, et le résultat voulu
est démontré. En outre, pour tout n  N, g(n)(0) = lim0h(n) = 0. Si g était, sur un
intervalle de la forme
N, g(n)(0) = lim0h(n) = 0. Si g était, sur un
intervalle de la forme ![]- r,r[](/numeros/RMS130-3/RMS130-31905x.png) avec r > 0, la somme d’une série entière, cette série entière
serait
avec r > 0, la somme d’une série entière, cette série entière
serait 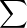
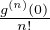 zn, donc g serait nulle au voisinage de 0, ce qu’elle n’est évidemment
pas.
zn, donc g serait nulle au voisinage de 0, ce qu’elle n’est évidemment
pas.
Ainsi, g n’est pas développable en série entière en 0.
b) Supposons l’existence de trois réels a,M,A strictement positifs tels que
![∀N ∈ N,∀x ∈ [- a,a],|f(N)(x)| ≤ M AN N!](/numeros/RMS130-3/RMS130-31908x.png)

![]- ρ,ρ[](/numeros/RMS130-3/RMS130-31909x.png) . Soit N
. Soit N  N. La fonction f(N+1) est donc bornée sur
le segment d’extrémités 0 et x par Mρ-(N+1)(N + 1)!. L’inégalité de Taylor-Lagrange donne
donc
N. La fonction f(N+1) est donc bornée sur
le segment d’extrémités 0 et x par Mρ-(N+1)(N + 1)!. L’inégalité de Taylor-Lagrange donne
donc
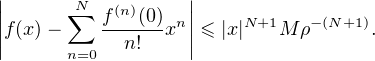
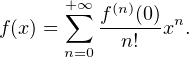
Réciproquement, supposons qu’il existe une suite réelle (cn)n≥0 et un r  R
R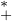 tels que
f(x) =
tels que
f(x) = 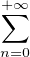 cnxn pour tout x
cnxn pour tout x 
![]- r,r[](/numeros/RMS130-3/RMS130-31914x.png) . Soit N
. Soit N  N. Alors f(N)(x) =
N. Alors f(N)(x) = 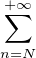 cn
cn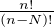 xn-N pour
tout x
xn-N pour
tout x 
![]-r,r[](/numeros/RMS130-3/RMS130-31917x.png) . Posons a :=
. Posons a := 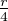 . Soit x
. Soit x  [-a,a]. Alors
[-a,a]. Alors
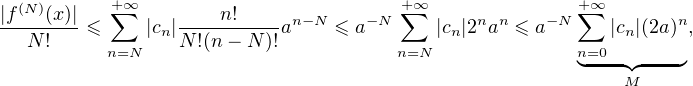
![(N ) -1 N
∀N ∈ N,∀x ∈ [- a,a],|f (x)| ≤ M (a ) N !](/numeros/RMS130-3/RMS130-31920x.png)
c) Fixons d’abord x > 0 et montrons que la fonction φ : h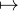 exp(-(x - h)-2) est la somme
d’une série entière sur le disque ouvert D := Do(0,x). Soit en effet h
exp(-(x - h)-2) est la somme
d’une série entière sur le disque ouvert D := Do(0,x). Soit en effet h  D. Par produit de Cauchy,
on trouve d’abord le développement
D. Par produit de Cauchy,
on trouve d’abord le développement
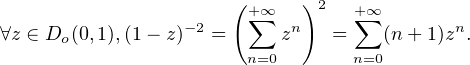
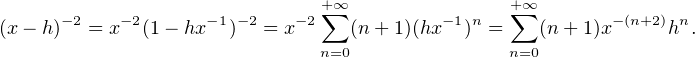
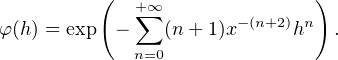
 N. Par produit de Cauchy de séries entières, il existe,
pour tout N
N. Par produit de Cauchy de séries entières, il existe,
pour tout N  N , une suite réelle positive (an,N)n
N , une suite réelle positive (an,N)n N telle que
N telle que
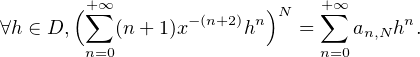
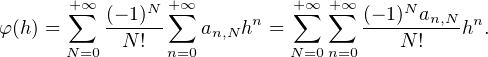
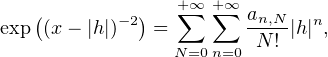
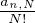 ≥ 0, la sommabilité de la famille
≥ 0, la sommabilité de la famille 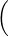
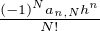
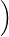 (N,n)
(N,n) N2. On déduit
donc du théorème de Fubini que si h≠0 alors
N2. On déduit
donc du théorème de Fubini que si h≠0 alors
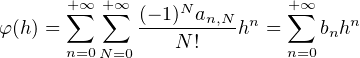
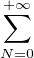
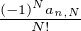 pour tout n
pour tout n  N (l’existence de bn étant garantie par le fait que hn≠0). En
particulier, comme D contient un élément non nul tous les bn sont bien définis, et le théorème de
Fubini donne encore φ(h) =
N (l’existence de bn étant garantie par le fait que hn≠0). En
particulier, comme D contient un élément non nul tous les bn sont bien définis, et le théorème de
Fubini donne encore φ(h) = 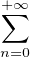 bnhn même si h = 0.
bnhn même si h = 0.
Ensuite, le théorème de dérivation d’une série entière indique que bn = (-1)n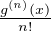 pour tout
n
pour tout
n  N .
N .
Fixons maintenant n  N* et exprimons différemment bn. Soit r
N* et exprimons différemment bn. Soit r 
![]0,x[](/numeros/RMS130-3/RMS130-31937x.png) . Alors,
. Alors,
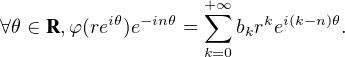
 R , et la série
R , et la série 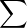 bkrk converge absolument car le rayon de convergence de
bkrk converge absolument car le rayon de convergence de 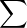 bkzk
est strictement supérieur à r. Ainsi, par intégration terme à terme sur un segment (avec terme
général continu), on obtient
bkzk
est strictement supérieur à r. Ainsi, par intégration terme à terme sur un segment (avec terme
général continu), on obtient
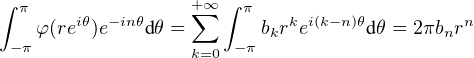
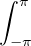 eikθ d θ = [(ik)-1eikθ]
eikθ d θ = [(ik)-1eikθ]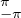 = 0 pour tout k
= 0 pour tout k  Z*. Ainsi,
Z*. Ainsi,
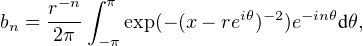
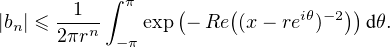
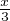 . Pour tout réel θ, on a donc
. Pour tout réel θ, on a donc
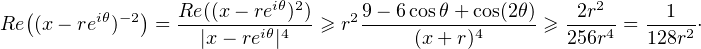
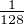 , on obtient
, on obtient
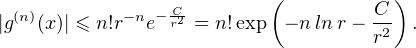
 R
R 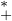
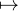 -nlnt-
-nlnt-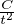 , fonction dérivable de dérivée ψʹ : t
, fonction dérivable de dérivée ψʹ : t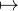 -
-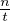 +
+ 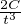 =
= 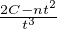 ⋅ On
en déduit facilement que ψ admet un maximum en
⋅ On
en déduit facilement que ψ admet un maximum en 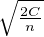 , de valeur
, de valeur 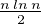 -
-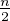 ln(2C) -
ln(2C) -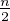 . En
posant B := (2C)-1⁄2, on en déduit que
. En
posant B := (2C)-1⁄2, on en déduit que
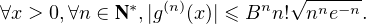
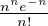 tend vers 0, et elle est donc
bornée par un réel D ≥ 1. Par suite, nne-n ≤ n!D ≤ n!Dn pour tout n ≥ 1. Ainsi, en posant
A := BD1⁄2 , on en déduit
tend vers 0, et elle est donc
bornée par un réel D ≥ 1. Par suite, nne-n ≤ n!D ≤ n!Dn pour tout n ≥ 1. Ainsi, en posant
A := BD1⁄2 , on en déduit
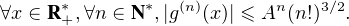
 N * . Comme g est paire on trouve ∀x
N * . Comme g est paire on trouve ∀x  R,g(n)(x) = (-1)ng(n)(-x). En outre
g(n) (0) = 0 comme vu en a) . Ainsi
R,g(n)(x) = (-1)ng(n)(-x). En outre
g(n) (0) = 0 comme vu en a) . Ainsi