 R2 tel que a < b, et g une fonction continue par morceaux de [a,b]
dans C . Montrer que
R2 tel que a < b, et g une fonction continue par morceaux de [a,b]
dans C . Montrer que 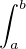 g(t)sin(λt)dt → 0 quand λ → +∞.
g(t)sin(λt)dt → 0 quand λ → +∞.
b) Soit f : R → C une fonction 2π-périodique de classe C1 par morceaux. Pour k  Z, on pose
ck =
Z, on pose
ck = 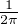
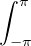 f(t)e-iktdt.
f(t)e-iktdt.
Montrer que pour tout réel t, 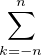 ckeikt tend vers
ckeikt tend vers 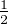
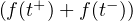 quand n tend vers
+ ∞.
quand n tend vers
+ ∞.
Solution d’après Moubinool Omarjee
a) Notons E l’espace vectoriel des fonctions continues par morceaux de [a,b] dans C. Pour g  E
et λ
E
et λ  R , posons Iλ(g) :=
R , posons Iλ(g) := 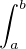 g(t)sin(λt)dt. Soit g : [a,b] → C en escalier, et (a0,…,an) une
subdivision de [a,b] adaptée à g. En notant yi := g
g(t)sin(λt)dt. Soit g : [a,b] → C en escalier, et (a0,…,an) une
subdivision de [a,b] adaptée à g. En notant yi := g
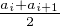
 pour tout i
pour tout i  {0,…,n - 1}, on a
donc : pour tout λ
{0,…,n - 1}, on a
donc : pour tout λ  R*,
R*,
![n∑-1 ∫ ai+1
Iλ(g)= (ai+1 - ai)yi sin(λt)dt
i=0 ai
1 n∑-1
= -- (ai+1 - ai)yi[- cos(λai+1) + cos(λai)] = O λ→+∞ (λ-1),
λ i=0](/numeros/RMS130-3/RMS130-31855x.png)
Soit g  E. Il existe une suite (gp)p
E. Il existe une suite (gp)p N de fonctions en escalier sur [a,b] convergeant uniformément
vers g. Pour tout p
N de fonctions en escalier sur [a,b] convergeant uniformément
vers g. Pour tout p  N et tout λ
N et tout λ  R, on voit que
R, on voit que
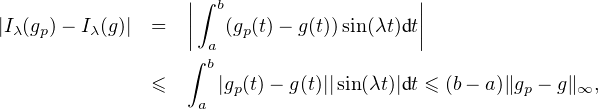
 Iλ(gp))p
Iλ(gp))p N vers λ
N vers λ Iλ(g). Or, pour tout
p
Iλ(g). Or, pour tout
p  N , on a vu que Iλ(gp) tend vers 0 quand λ tend vers + ∞. Par interversion des limites, on en
déduit que Iλ (g) tend vers 0 quand λ tend vers + ∞.
N , on a vu que Iλ(gp) tend vers 0 quand λ tend vers + ∞. Par interversion des limites, on en
déduit que Iλ (g) tend vers 0 quand λ tend vers + ∞.
b) Précisons la signification des hypothèses : une fonction g : R → C est dite de classe 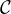 1 par
morceaux lorsqu’il existe, pour tout segment (non trivial) [a,b] de R, une subdivision (a0,…,an) de
[a, b] telle que, pour tout i
1 par
morceaux lorsqu’il existe, pour tout segment (non trivial) [a,b] de R, une subdivision (a0,…,an) de
[a, b] telle que, pour tout i  [ [0,n- 1]], la restriction de g à
[ [0,n- 1]], la restriction de g à ![]ai,ai+1[](/numeros/RMS130-3/RMS130-31859x.png) possède un prolongement de
classe
possède un prolongement de
classe 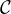 1 à [ai , ai+1]. On démontre aisément que pour une telle fonction f et n’importe quel réel τ,
la fonction gτ : t
1 à [ai , ai+1]. On démontre aisément que pour une telle fonction f et n’importe quel réel τ,
la fonction gτ : t g(t + τ) est encore de classe
g(t + τ) est encore de classe  1 par morceaux. Par ailleurs, une telle
fonction g est évidemment continue par morceaux. On aura enfin besoin du principe suivant,
dont la démonstration figure en annexe : étant donné une fonction 2π-périodique et
continue par morceaux g : R → C, l’intégrale
1 par morceaux. Par ailleurs, une telle
fonction g est évidemment continue par morceaux. On aura enfin besoin du principe suivant,
dont la démonstration figure en annexe : étant donné une fonction 2π-périodique et
continue par morceaux g : R → C, l’intégrale  gτ ne dépend pas du choix du réel
τ.
gτ ne dépend pas du choix du réel
τ.
Traitons d’abord le cas t = 0. Fixons n  N et posons Dn : θ
N et posons Dn : θ
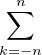 eikθ, fonction évidemment
paire. Par définition des ck et linéarité de l’intégrale, on trouve
eikθ, fonction évidemment
paire. Par définition des ck et linéarité de l’intégrale, on trouve
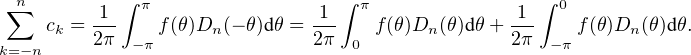 | (1) |
Notons que
![∫ π -ikθ -1 -ikθ π
e dθ = (- ik) [e ]-π = 0
-π](/numeros/RMS130-3/RMS130-31865x.png)
 Z * , tandis que
Z * , tandis que 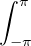 e-i0θdθ = 2π. On en déduit
e-i0θdθ = 2π. On en déduit 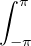 Dn = 2π, puis, par parité de Dn,
Dn = 2π, puis, par parité de Dn,
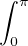 Dn =
Dn = 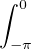 Dn. Par suite,
Dn. Par suite,
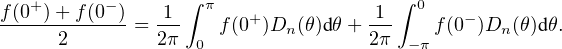 | (2) |
En combinant () et (), on obtient donc
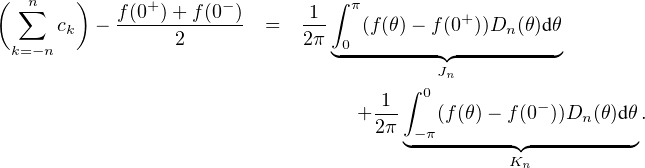

![]0,π]](/numeros/RMS130-3/RMS130-31872x.png) . Alors eiθ≠1 donc
. Alors eiθ≠1 donc
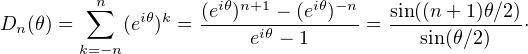
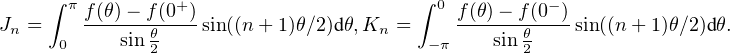
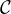 1 coïncidant avec f sur
1 coïncidant avec f sur ![]0,α[](/numeros/RMS130-3/RMS130-31875x.png) . En particulier g(0) = f(0+) donc
f(θ) - f(0+ ) = gʹ(0)θ + o(θ) quand θ tend vers 0. Puisque sin
. En particulier g(0) = f(0+) donc
f(θ) - f(0+ ) = gʹ(0)θ + o(θ) quand θ tend vers 0. Puisque sin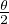 ~
~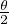 quand θ tend vers 0+, il
vient
quand θ tend vers 0+, il
vient
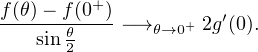

![]0,π]](/numeros/RMS130-3/RMS130-31879x.png)
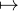
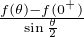 est alors clairement prolongeable en une fonction h+ : [0,π] → C
continue par morceaux On démontre de manière similaire que θ
est alors clairement prolongeable en une fonction h+ : [0,π] → C
continue par morceaux On démontre de manière similaire que θ 
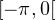
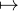
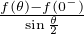 est
prolongeable en une fonction h- : [-π,0] → C continue par morceaux.
est
prolongeable en une fonction h- : [-π,0] → C continue par morceaux.
On voit alors, avec les notations de a) , que Jn = In+1⁄2(h+) et Kn = In+1⁄2(h-) pour tout
n  N . Le résultat établi en a) montre alors que (Jn)n et (Kn)n convergent vers 0, et on conclut
que
N . Le résultat établi en a) montre alors que (Jn)n et (Kn)n convergent vers 0, et on conclut
que
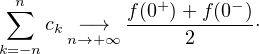
Terminons par le cas général. Soit t  R. La fonction ft est alors de classe
R. La fonction ft est alors de classe 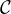 1 par morceaux, et
ft (0+ ) = f(t+ ) et ft(0-) = f(t-). Enfin, pour tout k
1 par morceaux, et
ft (0+ ) = f(t+ ) et ft(0-) = f(t-). Enfin, pour tout k  Z, comme la fonction θ
Z, comme la fonction θ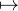 f(θ)e-ikθ
est clairement continue par morceaux et 2π-périodique, le résultat démontré en annexe
donne
f(θ)e-ikθ
est clairement continue par morceaux et 2π-périodique, le résultat démontré en annexe
donne
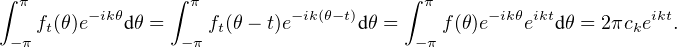
Annexe : intégrale sur une période
Une difficulté est que le programme de Mathématiques de la filière MPSI/MP ne fournit aucune
formule de changement de variable lorsque l’intégrande est seulement supposé continu par
morceaux ! Nous allons commencer par combler cette lacune pour un changement de variable
translatif : soit en effet h : [a,b] → C continue par morceaux, (a0,…,an) une subdivision adaptée,
et τ  R . Montrons que
R . Montrons que
![∫ ∫
hτ = h.
[a-τ,b-τ] [a,b]](/numeros/RMS130-3/RMS130-31889x.png) | (3) |
D’abord
![∫ b n-1 ∫ a n- 1∫
h = ∑ i+1h = ∑ h.
a i=0 ai i=0 ]ai,ai+1[](/numeros/RMS130-3/RMS130-31890x.png)
![∫ b-τ n∑-1 ∫ ai+1-τ n∑-1∫
hτ = h = hτ.
a-τ i=0 ai-τ i=0 ]ai-τ,ai+1-τ[](/numeros/RMS130-3/RMS130-31891x.png)
![∫
]ai-τ,ai+1-τ[](/numeros/RMS130-3/RMS130-31892x.png) hτ =
hτ = ![∫
]ai,ai+1[](/numeros/RMS130-3/RMS130-31893x.png) h pour tout i
h pour tout i  [ [0,n - 1]]. On en déduit
().
[ [0,n - 1]]. On en déduit
().
Pour finir, soit h : R → C continue par morceaux et 2π-périodique. Soit a  R. Alors
R. Alors
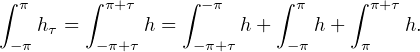
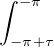 h =
h = 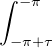 h2π =
h2π = 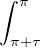 h = -
h = -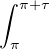 h, et on conclut
que
h, et on conclut
que 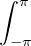 hτ =
hτ = 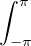 h.
h.

