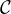 0([0,1], R). Une suite (gn)n
0([0,1], R). Une suite (gn)n N
N  EN est appelée base de
type S lorsque, pour tout f
EN est appelée base de
type S lorsque, pour tout f  E, il existe une unique suite (cn)n
E, il existe une unique suite (cn)n N
N  RN telle que
f =
RN telle que
f = 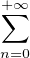 cngn avec convergence uniforme.
cngn avec convergence uniforme.
a) Montrer qu’il existe une suite (xn)n N d’éléments deux à deux distincts de [0,1] telle que
x0 = 0, x1 = 1, et {xn∣n
N d’éléments deux à deux distincts de [0,1] telle que
x0 = 0, x1 = 1, et {xn∣n  N} soit dense dans [0,1].
N} soit dense dans [0,1].
b) Soit (gn )n N une base de type S. Montrer que
N une base de type S. Montrer que 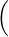
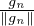
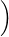 n
n N est une base de type
S.
N est une base de type
S.
c) Soit f  E. Pour tout n
E. Pour tout n  N*, on note Fn la fonction de [0,1] dans R qui est continue, affine
sur chaque intervalle ouvert inclus dans [0,1] \{x0,…,xn}, et coïncide avec f en x0,…,xn.
Montrer que (Fn)n≥1 converge uniformément vers f sur [0,1].
N*, on note Fn la fonction de [0,1] dans R qui est continue, affine
sur chaque intervalle ouvert inclus dans [0,1] \{x0,…,xn}, et coïncide avec f en x0,…,xn.
Montrer que (Fn)n≥1 converge uniformément vers f sur [0,1].
d) En déduire l’existence d’une base de type S.
a) On pose x0 = 0, x1 = 1 et on introduit une indexation dénombrable (xn)n≥2 des rationnels de ]0, 1[.
b) Notons que les gn sont non nuls, en raison de l’unicité de la décomposition. Posons hn := 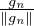 .
Alors tout élément f
.
Alors tout élément f  E s’écrit f =
E s’écrit f = 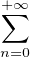 cn∥gn∥hn, avec convergence uniforme, et il y a
évidemment unicité de l’écriture.
cn∥gn∥hn, avec convergence uniforme, et il y a
évidemment unicité de l’écriture.
c) On a Fn (xk ) = f(xk) pour k ≤ n. De plus, Fn est continue. Tout revient à montrer, par différence, que si gn := f - Fn, alors (gn) converge uniformément vers 0.
Soit ϵ > 0 et η > 0 relatif à l’uniforme continuité de f sur [0,1]. On peut trouver, par densité, des
éléments x0 < xn2 <  < xnp < x1 formant une subdivision de pas moindre que η. On pose
n0 := 0 et n1 := 1. Soit N := max(nk), et n ≥ N. Soit x
< xnp < x1 formant une subdivision de pas moindre que η. On pose
n0 := 0 et n1 := 1. Soit N := max(nk), et n ≥ N. Soit x  [0,1]. Il existe k ≤ p - 1 tel que
x
[0,1]. Il existe k ≤ p - 1 tel que
x  [xnk , xnk+1 ]. On a alors
[xnk , xnk+1 ]. On a alors
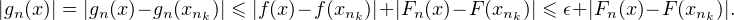
Comme Fn est affine sur [xnk,xnk+1],
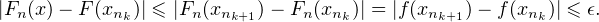
Par suite, pour n ≥ N, et pour tout x  [0,1], |gn(x)|≤ 2ϵ.
[0,1], |gn(x)|≤ 2ϵ.
d) Notons, pour n ≥ 1, fn la fonction affine par morceaux qui vaut 1 en xn et 0 en x0,…,xn-1 : elle est donc nulle sur tout intervalle de la subdivision formée par x0,…,xn sauf sur les deux (pour n ≥ 2) intervalles dont xn est une extrémité. On note f0 la fonction affine égale à 1 en 0 et 0 en 1.
Considérons la fonction Gn(f) = Fn(f) -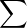
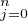 λj,nfj et déterminons les λk,n de façon que
Gn (f) s’annule en x0,…,xn. Ceci équivaut à f(x0) = λ0,n et
λj,nfj et déterminons les λk,n de façon que
Gn (f) s’annule en x0,…,xn. Ceci équivaut à f(x0) = λ0,n et
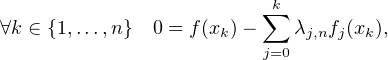
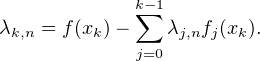
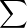
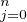 λjfj s’annule donc en x0,…,xn. Elle est affine sur chacun des intervalles de la
subdivision associée. Elle est donc nulle. Ainsi,
λjfj s’annule donc en x0,…,xn. Elle est affine sur chacun des intervalles de la
subdivision associée. Elle est donc nulle. Ainsi,
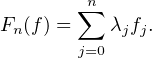
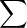
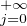 λjfj, la convergence étant uniforme sur [0,1].
λjfj, la convergence étant uniforme sur [0,1].
Enfin, supposons que les μj soient tels que 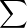
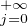 μjfj = 0, la convergence étant uniforme. En
évaluant en x0 , on obtient : μ0 = 0. Si l’on suppose par récurrence que μ0 =
μjfj = 0, la convergence étant uniforme. En
évaluant en x0 , on obtient : μ0 = 0. Si l’on suppose par récurrence que μ0 =  = μk-1 = 0,
alors l’égalité μk = 0 découle de l’évaluation en xk.
= μk-1 = 0,
alors l’égalité μk = 0 découle de l’évaluation en xk.
Une famille de type S se nomme une base de Schauder. L’exercice fait montrer que l’espace
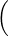
 0([0,1], R),∥⋅∥∞
0([0,1], R),∥⋅∥∞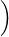 admet une telle base. L’intéressant, c’est que l’on peut démontrer que tout
espace de Banach (E,∥⋅∥) admettant une partie dénombrable dense se plonge isométriquement
dans l’espace précédent, et donc que tout espace de Banach peut être considéré comme un
sous-espace fermé d’un espace admettant une base de Schauder. Malheureusement, ceci n’implique
pas que E admette une base de Schauder : il y a de (trop) nombreux contre-exemples.
admet une telle base. L’intéressant, c’est que l’on peut démontrer que tout
espace de Banach (E,∥⋅∥) admettant une partie dénombrable dense se plonge isométriquement
dans l’espace précédent, et donc que tout espace de Banach peut être considéré comme un
sous-espace fermé d’un espace admettant une base de Schauder. Malheureusement, ceci n’implique
pas que E admette une base de Schauder : il y a de (trop) nombreux contre-exemples.

