303. Soit I un intervalle de R non trivial.

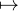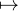a) Montrer qu’il n’existe pas de R ∈ R(X) sans pôle dans I tel que x ∈ I↦→R(x)e-x2 soit une primitive de x ∈ I↦→e-x2 .

b) Soient G ∈ R (X) sans pôle dans I, H ∈ R[X,Y ].

On suppose : ∀x ∈ I,H(x,eG(x)) = 0. Montrer que H = 0.

a) Si R vérifie que 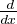ddxR(x)e-x2 = e-x2 , on a aussi Rʹ- 2xR = 1. Soit a un pôle complexe de R, de multiplicité m. Grâce à la décomposition de R en éléments simples, on peut écrire

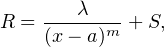
R = ----λ--- +S, (x - a)m
où S admet le pôle a à un ordre inférieur ou égal à m - 1. Donc
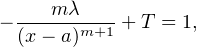
----mλ---- -(x - a)m+1 + T = 1,
où T admet a pour pôle de multiplicité au plus m : c’est une contradiction. Ainsi, R n’a pas de pôle. C’est donc un polynôme, ce qui est interdit pour une question de degré.

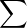
b) Posons f := eG. Soit H ∈ R(X)[Y ], que l’on écrit H = ∑kRkY k, les Rk étant dans R(X). Montrons que si H est tel que H(x,f(x)) = 0 pour tout x dans un intervalle de longueur strictement positive ne contenant aucun pôle d’aucun Rk ni de G, alors H = 0.

Supposons le contraire. Parmi les H précédents, il en existe un dont le degré en Y , noté m, est minimal. Bien sûr, m ≥ 1. On note I l’intervalle correspondant et toujours H le polynôme. Dérivons. Pour tout x

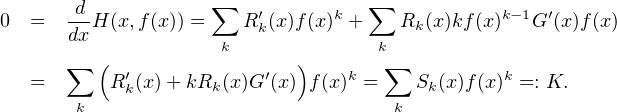
0=dH (x,f(x)) = ∑ Rʹ(x)f(x)k + ∑ R (x)kf(x)k- 1G ʹ(x)f(x) dx k k k k ∑ ( ) ∑ = R ʹk(x)+ kRk (x)G ʹ(x) f(x)k = Sk(x)f(x)k =: K. k k

Les Sk n’ont aucun pôle dans I. Puisque 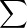∑kSk(X)Y k est de degré en Y moindre que m, ce polynôme est soit le polynôme nul, soit de degré m.

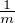
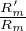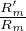∙ Si c’est le polynôme nul, on a en particulier Rʹm + mRmGʹ = 0, donc Gʹ = -1- mRʹm- Rm. Mais un pôle complexe de G est un pôle multiple de Gʹ, tandis que ʹ RRmm n’a que des pôles simples. Donc G n’a pas de pôle, donc est un polynôme, ce qui entraîne que Rm est une constante, donc que Gʹ = 0, ce qui a été exclu.

∙ Si ce n’est pas le polynôme nul, considérons S := (Rʹm + mRmGʹ)H - RmK. Le coefficient de Y m est nul, et S(x,f(x)) = 0 sur I. Donc S = 0. Il en résulte que, pour tout k,

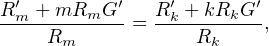
R ʹm + mRmG ʹ R ʹ+ kRkG ʹ -----R------ = --k-R------, m k
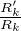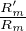soit (m - k)Gʹ = ʹ RkRk - ʹ RRmm. nouveau, G n’a pas de pôle complexe, puis est une constante, ce qui est une contradiction.

Bien entendu, la question b) n’est rien d’autre qu’un résultat sur les fonctions algébriques sur C(x). La petite difficulté de rédaction provient du fait que C(x) n’est pas véritablement un corps, puisque les fractions rationnelles, en tant que fonctions, ne sont pas définies sur le même ensemble.
[Liste des corrigés]


[ < ]