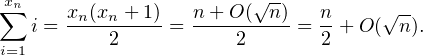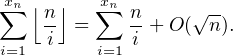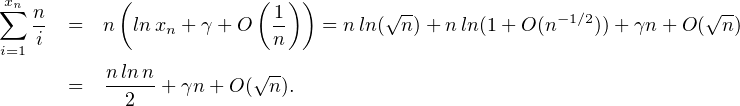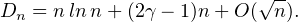N* on note d(k) le nombre de diviseurs positifs de k.
N* on note d(k) le nombre de diviseurs positifs de k.
a) Donner un équivalent de Dn = 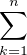 d(k).
d(k).
b) On note γ la constante d’Euler. Montrer que Dn = nlnn + (2γ - 1)n + O(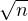 ).
).
Solution de Moubinool Omarjee et Adrien Reisner
On aura besoin du développement eulérien classique
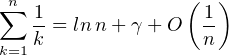
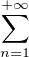 un pour la suite u définie par u1 := 1 et un :=
un pour la suite u définie par u1 := 1 et un := 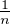 -
-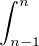
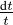 pour tout entier n ≥ 2. La
convergence de la série découle du théorème de comparaison série-intégrale puisque t
pour tout entier n ≥ 2. La
convergence de la série découle du théorème de comparaison série-intégrale puisque t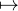
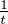 est
continue par morceaux, décroissante et positive sur
est
continue par morceaux, décroissante et positive sur 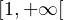 . Le développement annoncé s’obtient
alors par simple récriture de la somme partielle
. Le développement annoncé s’obtient
alors par simple récriture de la somme partielle 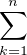 uk.
uk.
Étant donné n  N*, on notera
N*, on notera 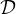 (n) l’ensemble des diviseurs positifs de n et
(n) l’ensemble des diviseurs positifs de n et
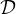 - (n) :=
- (n) := 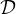 (n) ∩
(n) ∩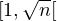 .
.
a) En sommant par paquets, on trouve
![∑n ∑ ∑ n∑ ∑
Dn = 1 = 1 = 1.
k=1i∈D(k) (k,i)∈[[1,n]]2t.q.i|k i=1 k∈[[1,n]]t.q.i|k](/numeros/RMS130-3/RMS130-31754x.png)
 [ [1,n]], la fonction p
[ [1,n]], la fonction p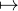 ip réalise une bijection de
ip réalise une bijection de 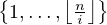 sur
l’ensemble des multiples de i dans [ [1,n]]. Ainsi, Dn =
sur
l’ensemble des multiples de i dans [ [1,n]]. Ainsi, Dn = 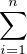
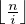 . Par inégalité triangulaire, il
vient
. Par inégalité triangulaire, il
vient
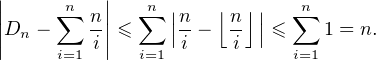
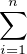
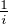 + O(n) et finalement, grâce au développement eulérien rappelé en
introduction :
+ O(n) et finalement, grâce au développement eulérien rappelé en
introduction :
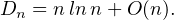
b) Nous raffinons la méthode précédente. Soit n  N*. La fonction k
N*. La fonction k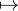
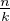 réalise une bijection de
réalise une bijection de
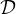 - (n) sur
- (n) sur 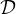 (n) ∩
(n) ∩![√ --
] n,+∞ [](/numeros/RMS130-3/RMS130-31765x.png) . On en déduit que d(n) = 2card
. On en déduit que d(n) = 2card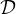 -(n) + 1 si n est un carré, et
d(n) = 2 card
-(n) + 1 si n est un carré, et
d(n) = 2 card 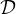 -(n) sinon.
-(n) sinon.
Fixons n  N * . Le nombre de carrés dans [ [1,n]] est évidemment ⌊
N * . Le nombre de carrés dans [ [1,n]] est évidemment ⌊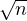 ⌋, donc
⌋, donc
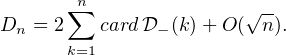
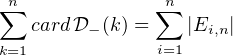
 [ [ 1, n]], on a noté Ei,n l’ensemble des k
[ [ 1, n]], on a noté Ei,n l’ensemble des k  [ [1,n]] tels que i divise k et i <
[ [1,n]] tels que i divise k et i < 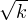 ,
autrement dit i divise k et i <
,
autrement dit i divise k et i < 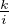 . En procédant comme en a) , on voit que k
. En procédant comme en a) , on voit que k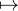
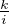 met en bijection
Ei,n avec l’ensemble des entiers l tels que i < l ≤
met en bijection
Ei,n avec l’ensemble des entiers l tels que i < l ≤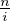 . Ce dernier ensemble est vide si i >
. Ce dernier ensemble est vide si i > 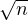 , sinon
il est de cardinal
, sinon
il est de cardinal 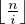 - i. Il vient
- i. Il vient
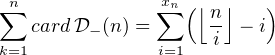
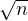 ⌋. On remarquera que x
n =
⌋. On remarquera que x
n = 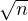 + O(1) en vue de la suite. D’une part
+ O(1) en vue de la suite. D’une part