 N * , M(f)(n) =
N * , M(f)(n) = 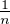
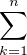 f(k).
f(k).
a) Montrer que, pour toute fonction f de N* dans R, ∀n  N*,M(k)(f)(n)
N*,M(k)(f)(n)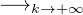 f(1).
f(1).
b) Montrer que, si f est polynomiale, il en est de même de M(f).
Solution de Mohamed Houkari
a) Fixons n  N*. Pour toute application f : N*→
N*. Pour toute application f : N*→  et tout n
et tout n  N*, on a
N*, on a
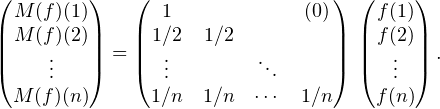
On note A = 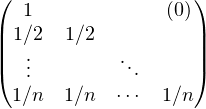 et u l’endomorphisme de
et u l’endomorphisme de  n canoniquement associé à
A. L’endomorphisme u est alors diagonalisable (car A est triangulaire inférieure et compte n valeurs
propres distinctes).
n canoniquement associé à
A. L’endomorphisme u est alors diagonalisable (car A est triangulaire inférieure et compte n valeurs
propres distinctes).
On pose e =  et H l’hyperplan engendré par les vecteurs
et H l’hyperplan engendré par les vecteurs  ,
,  , ...,
, ...,  ,
c’est-à-dire les (n - 1) derniers vecteurs de la base canonique de
,
c’est-à-dire les (n - 1) derniers vecteurs de la base canonique de  n.
n.
On a alors les faits suivants :
 n =
n =  ⋅ e ⊕ H
⋅ e ⊕ H
- e est vecteur propre de u pour la valeur propre 1
- H est stable par u et l’endomorphisme induit par u sur H a pour valeurs propres
 ,
,  ,…,
,…, .
.
Soit une application f : N* →  et un entier n
et un entier n  N*. On pose X =
N*. On pose X = 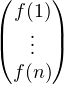 et on
écrit
et on
écrit
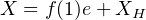
avec XH  H. Alors,
H. Alors,
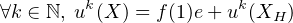
Or uk (XH )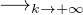 0 puisque l’induit par u sur H est diagonalisable à valeurs propres dans
]-1 , 1[.
0 puisque l’induit par u sur H est diagonalisable à valeurs propres dans
]-1 , 1[.
Ainsi, uk (X)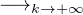 f(1)e, donc, pour ce qui est de sa n-ième composante :
f(1)e, donc, pour ce qui est de sa n-ième composante :
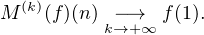
b) Par linéarité, il suffit de montrer que, pour tout k  N, l’application M(fk) associée à
fk : n
N, l’application M(fk) associée à
fk : n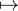 nk est polynomiale. Fixons k
nk est polynomiale. Fixons k  N. On a :
N. On a :
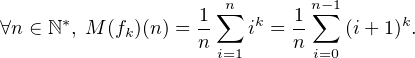
La question fait directement référence à un résultat classique concernant les sommes de puissances d’entiers consécutifs. L’endomorphisme
![{
Δ : Rk+1[X] -→ Rk+1[X]
P ↦-→ P(X + 1)- P (X )](/numeros/RMS130-3/RMS130-31739x.png)
a pour image  k [X] et pour noyau
k [X] et pour noyau  0[X], ce qui montre qu’il existe un unique Qk
0[X], ce qui montre qu’il existe un unique Qk 
 k+1[X]
vérifiant Qk (0) = 0 et Δ(Qk) = (X + 1)k.
k+1[X]
vérifiant Qk (0) = 0 et Δ(Qk) = (X + 1)k.
Ainsi
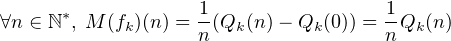
Or Qk (0) = 0, donc 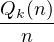 est une expression polynomiale en n.
est une expression polynomiale en n.
Ainsi, pour tout k  N, l’application M(fk) est polynomiale, ce qui démontre le résultat
voulu.
N, l’application M(fk) est polynomiale, ce qui démontre le résultat
voulu.
[Liste des corrigés]

