5. Si n ∈ N * , soit σ(n) la somme des diviseurs de n dans N*. On dit qu’un élément P ∈ N* est parfait si σ(P) = 2P .

a) Soit p ∈ N * tel que 2p - 1 est premier. Montrer que p est premier.

b) Montrer que, si p est un élément de N* tel que 2p - 1 est premier, alors 2p-1(2p - 1) est parfait.

On admet dans la suite que tout nombre parfait pair est de la forme précédente. On considère un nombre parfait pair, que l’on écrit donc sous la forme P = 2p-1(2p - 1) où p ∈ N * est tel que 2p - 1 est premier. Dans les question c), d), e) , on suppose p≠ 2.

c) Déterminer la classe de P modulo 12.

d) Montrer que P - 1 et P + 1 ne sont pas des carrés.

e) En considérant la classe de P - 1 modulo 4 et celle de P + 1 modulo 3, montrer que P - 1 et P + 1 ne sont pas parfaits.

f) Montrer qu’il n’existe pas de couple de nombres parfaits consécutifs.

g) Prouver le résultat admis.

a) Si p n’est pas premier, posons p = qr avec 2 ≤ q ≤ p - 1. On a

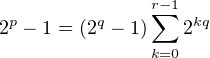
r-∑ 1 2p - 1 = (2q - 1) 2kq k=0
dont 2p - 1 n’est pas premier, ce qui est absurde.

b) Comme 2p-1 ∧ (2p - 1) = 1, on a

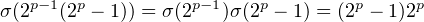
p- 1 p p-1 p p p σ(2 (2 - 1)) = σ (2 )σ(2 - 1) = (2 - 1)2

ce qui montre que 2p-1(2p - 1) est parfait.

c) Comme p ≥ 3, 2p-1 ≡ 0 (mod 4). Comme p- 1 est pair, 2p-1 ≡ 1 (mod 3). Ainsi 2p-1 ≡ 4 (mod 12) et P = 2p-1(2p - 1) ≡ 4 × 7 (mod 12), soit P ≡ 4 (mod 12).

d) Les carrés de (Z⁄12Z,+,×) sont 0,1,4 et 9, donc ni P - 1, ni P + 1 ne sont des carrés dans (Z ⁄12Z , +, ×). A fortiori ni P - 1, ni P + 1 ne sont des carrés dans Z.

e) Montrons que P - 1 n’est pas parfait. Comme P - 1 n’est pas un carré, l’ensemble des diviseurs de P - 1 est

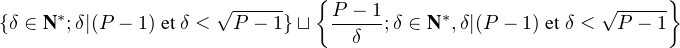
{ } {δ∈N*;δ|(P- 1)etδ < √P---1}⊔ P---1;δ ∈ N *,δ|(P - 1)etδ < √P-- 1 δ

Ainsi

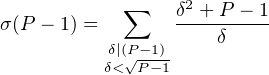
σ(P - 1) = ∑ δ2 +-P---1 δ|(P -1) δ δ<√P--1

Or, puisque P - 1 ≡ 3 (mod 4), si δ divise P - 1, δ est impair et donc δ2 + P - 1 ≡ 0 (mod 4) et 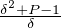2 δ+P-1δ ≡ 0 (mod 4). Ainsi σ(P - 1) ≡ 0 (mod 4). Or 2(P - 1) ≡ 2 (mod 4), donc σ(P - 1)≠ 2(P - 1) et P - 1 n’est pas parfait.

Montrons maintenant que P + 1 n’est pas parfait. Le raisonnement est analogue en considérant des congruences modulo 3. On a

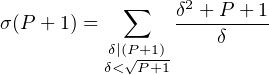
∑ δ2 +-P-+-1 σ(P + 1) = δ δδ|<(P√P+1)+1

Si δ divise P + 1, puisque P + 1 ≡ 2 (mod 3), on a δ ≡ 1 ou 2 (mod 3) et donc δ2 + P + 1 ≡ 0 (mod 3) et 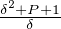δ2+P+1 δ ≡ 0 (mod 3). Ainsi σ(P + 1) ≡ 0 (mod 3). Or 2(P + 1) ≡ 1 (mod 3), donc σ(P + 1)≠ 2(P + 1) et P + 1 n’est pas parfait.

f) Raisonnons par l’absurde en considérant n ∈ N* tel que n et n + 1 sont parfaits.

∙ Si n est pair, on dispose de p premier tel que n = 2p-1(2p - 1). On a p≠2 puisque 7 n’est pas parfait, donc p ≥ 3, mais alors d’après e) , n + 1 n’est pas parfait. C’est absurde.

∙ Si n est impair, on dispose de p premier tel que n + 1 = 2p-1(2p - 1). On a p≠2 puisque 5 n’est pas parfait, donc p ≥ 3, mais alors d’après e) , n = (n + 1) - 1 n’est pas parfait. C’est absurde.

Ainsi, il n’existe pas de couples constitué de deux nombres parfaits consécutifs.

g) Considérons N un nombre pair parfait et établissons l’existence de p premier tel que 2p - 1 est premier et N = 2p-1(2p - 1).

On pose N = 2Q (2m + 1) avec Q ∈ N* et m ∈ N. Alors

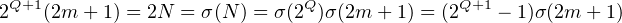
Q+1 Q Q+1 2(2m+ 1) = 2N = σ(N) = σ(2 )σ (2m + 1) = (2 - 1)σ (2m + 1)

Comme 2Q+1 - 1 et 2Q+1 sont premiers entre eux, on dispose de T ∈ N* tel que 2m + 1 = (2Q+1 - 1)T et σ(2m + 1) = 2Q+1T .

Supposons T≠ 1. Alors

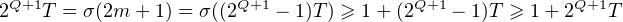
Q+1 Q+1 Q+1 Q+1 2T=σ (2m + 1) = σ((2 - 1)T ) ≥ 1+ (2 - 1)T ≥ 1 +2 T

ce qui est absurde. Donc T = 1 et N = 2Q(2Q+1 - 1). Comme N est parfait, on en déduit que σ(2Q+1 - 1) = 2Q+1, ainsi 1 et 2Q+1 - 1 sont les seuls diviseurs de 2Q+1 - 1 qui est donc premier ; selon a) , Q + 1 est premier. Posons alors p = Q + 1 ; on a N = 2p-1(2p - 1) avec p et 2p - 1 premiers.

Note : ∙ On ignore s’il existe des nombres parfaits impairs.

∙ Les nombres premiers de la forme 2p - 1 sont appelés les nombres de Mersenne ; on ignore s’ils sont en nombre infini. Les plus grands nombres premiers connus actuellement sont des nombres de Mersenne.
[Liste des corrigés]


[ < ]