284. Soient θ1 , θ2,…,θn  R avec 0 < θ1 < θ2 <
R avec 0 < θ1 < θ2 <  < θn < 1 et a1,…,an
< θn < 1 et a1,…,an  R. On suppose
que la suite de terme général up =
R. On suppose
que la suite de terme général up = 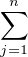 aj cos(πpθj) tend vers 0. Montrer : ∀j
aj cos(πpθj) tend vers 0. Montrer : ∀j  {1,…,n},
aj = 0.
{1,…,n},
aj = 0.
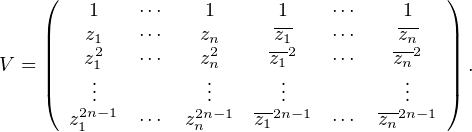
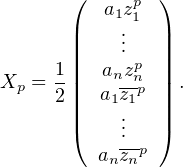
 R avec 0 < θ1 < θ2 <
R avec 0 < θ1 < θ2 <  < θn < 1 et a1,…,an
< θn < 1 et a1,…,an  R. On suppose
que la suite de terme général up =
R. On suppose
que la suite de terme général up = 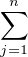 aj cos(πpθj) tend vers 0. Montrer : ∀j
aj cos(πpθj) tend vers 0. Montrer : ∀j  {1,…,n},
aj = 0.
{1,…,n},
aj = 0.
Posons pour tout j  [ [1,n]], zj = eiπθj et considérons la matrice de Vandermonde :
[ [1,n]], zj = eiπθj et considérons la matrice de Vandermonde :
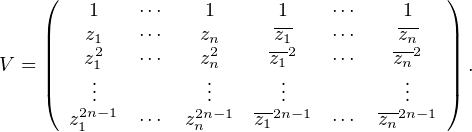
Comme 0 < θ1 < θ2 <  < θn < 1, les nombres complexes z1,
< θn < 1, les nombres complexes z1, ,zn,z1,
,zn,z1, ,zn sont tous
distincts, donc V
,zn sont tous
distincts, donc V  GL2n(C). Soit pour p
GL2n(C). Soit pour p  N la matrice colonne :
N la matrice colonne :
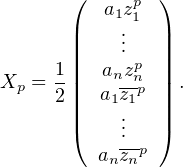
Pour tout p  N , V Xp =
N , V Xp =  , donc par hypothèse : limp→+∞V Xp = 0.
, donc par hypothèse : limp→+∞V Xp = 0.
Or, pour tout p, Xp = V -1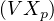 donc
donc 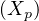 p
p N converge vers 0. Les nombres complexes zj
étant tous de module 1, on en déduit que : ∀j
N converge vers 0. Les nombres complexes zj
étant tous de module 1, on en déduit que : ∀j  {1,…,n}, aj = 0.
{1,…,n}, aj = 0.

