283. Soient C l’algèbre des fonctions continues de [0,1] dans R, A une sous-algèbre de C, A l’adhérence de A pour la norme ∥∥∞.

a) Montrer que, si f et g sont dans A, il en est de même de min(f,g).

b) Soient m ∈ N *, f1,…,fm dans A. Montrer que min(f1,…,fm) et max(f1,…,fm) sont dans A .

On suppose désormais que A sépare les points : pour a et b dans [0,1] distincts, il existe f ∈ A telle que f(a)≠ f(b).

c) Soient a et b deux éléments distincts de [0,1], α et β deux nombres réels. Montrer qu’il existe f ∈ A tel que f(a) = α et f(b) = β.

On admet que, de tout recouvrement ouvert de [0,1], on peut extraire un recouvrement fini.

d) Soit f ∈ C. Montrer que, pour ε ∈ R+* et x ∈ [0,1], il existe gx ∈A telle que gx(x) = f(x) et gx ≤ f + ε.

e) Montrer que A = C.

Solution de Nguyên Hai Châu

a) Remarquons tout d’abord que A est une sous-algèbre fermée de C (vérification sans difficulté), et que si f ∈ A alors P • f ∈A pour tout P ∈ R[X].

Grâce aux relations

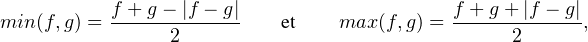
min(f,g) = f +-g--|f --g| et max (f,g) = f-+-g+-|f --g|, 2 2
on voit qu’il suffit de prouver que si f ∈A, alors |f|∈A.

Puisque f est continue sur [0,1], son image est un segment [a,b]. La fonction v : x↦→|x| est continue, il existe donc une suite (Pn) de polynômes qui converge uniformément vers v sur [a, b]. Ainsi, Pn • f converge uniformément vers |f| sur [0,1], si bien que |f| ∈ A .

b) Récurrence immédiate.

c) Il existe h ∈ A tel que h(a)≠h(b). On considère le polynôme interpolateur de Lagrange tel que P(h(a)) = α et P(h(b)) = β. Alors P • h ∈ A convient.

d) Fixons ε > 0 et x ∈ [0,1]. Pour chaque y≠x, on trouve une fonction fy ∈ A telle que fy (x) = f(x) et fy(y) = f(y). On considère l’ensemble

Ω = {z ∈ [0,1], f(z) < f (z)+ ε}, y y
c’est un ouvert de [0, 1] contenant x et y. La famille (Ωy)y≠x est un recouvrement ouvert de [0,1]. Il existe donc, d’après le résultat admis, des points y1,...,yn≠x tels que :
n [0,1] = ⋃ Ωy . i=1 i

N.B. Il s’agit d’ouverts relatifs de [0,1]. Si l’on veut travailler avec des ouverts de R, il suffit de remplacer Ωy par Ωy ∪ (R \ [0,1]).

On considère alors la fonction gx = min(fy1,...,fyn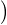)∈A. On a gx(x) = f(x). De plus, si z ∈ [0, 1], il existe i ∈{1,...,n } tel que z ∈ Ωyi ; on a donc :

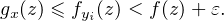
gx(z) ≤ fyi(z) < f(z) + ε.

e) On raisonne de la même manière. On dispose des fonctions gx ∈A telle que gx(x) = f(x) et gx < f + ε. On considère, pour tout x ∈ [0,1],

Ux = {z ∈ [0,1], gx(z) > f(z)- ε},

c’est un ouvert relatif de [0,1] qui contient x. Ainsi, la famille (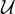Ux)x∈[0,1] est un recouvrement ouvert de [0, 1]. Il existe donc x1,...,xp ∈ [0,1] tels que :

p [0,1] = ⋃ Ux . i=1 i

On considère finalement g = max(gx1,...,gxp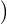)∈A. Alors, on a : ∀z ∈ [0,1],h(z) < f(z) + ε. Mais d’autre part, pour chaque z ∈ [0,1], il existe i ∈{1,...,p} tel que z ∈Uxi et donc : f(z) - ε < gxi (z) ≤ g(z), d’où

| | ∀z ∈ [0,1],|g(z)- f(z)| ≤ ε.

Ainsi f ∈ A et on a prouvé que A = C.

Le résultat démontré dans cet exercice est le théorème de Stone-Weierstrass.


[Liste des corrigés]


[ < ]