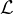275. On pose C = [-1,1]2. Soit f ∈L(R2). Étudier la suite (fn)n≥0 sous les hypothèses suivantes : i) f(C) ⊂ [-1⁄2,1⁄2]2 ; ii) f(C) ⊂]- 1,1[2 ; iii) f(C) ⊊ C.

Solution d’après Christophe Jan

On munit R 2 de la norme infinie ∥-∥∞. On remarque que C est la boule unité fermée pour cette norme. On utilisera la norme d’opérateur définie comme suit : pour u ∈L(R2),

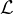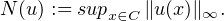
N (u) := supx∈C ∥u(x)∥∞.
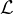Classiquement, N est une norme sur L(R2) et on dispose de l’identité
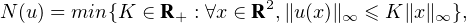
N (u) = min{K ∈ R+ : ∀x ∈ R2,∥u(x)∥∞ ≤ K∥x∥∞ },
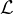d’où l’on tire, pour tous u,v dans L(R2), l’inégalité
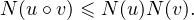N (u •v) ≤ N (u)N (v).
(1)

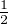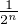i) On suppose que f(C) ⊂[ ] - 12, 122. On a donc immédiatement N(f) ≤12. En utilisant (), il vient par récurrence N(fn) ≤12n- pour tout n ∈ N* , donc (fn)n converge vers 0.

ii) On suppose que f(C) ⊂]- 1,1[2. Comme f est continue et C est compact (non vide), x↦→ ∥f(x)∥∞ possède un maximum M sur C. On en déduit que N(f) < 1, et comme dans la situation (i) cela permet de voir que (fn)n converge vers 0.

iii) On suppose que f(C) ⊊ C. En particulier N(f) ≤ 1, donc N(fn) ≤ 1 pour tout n ∈ N*, aussi (fn )n est bornée.

On notera A la matrice de f dans la base canonique B. Toutes les applications linéaires (respectivement, bilinéaires) considérées dans la suite ont pour espace de départ un espace vectoriel de dimension finie (resp. un produit de tels espaces) : pour justifier leur continuité, on fera donc simplement mention de leur linéarité (resp. de leur bilinéarité).

Nous commençons par un premier résultat élémentaire :

  • Toutes les racines de χf sont dans Df(0,1).

Soit en effet λ une racine de χf. Il existe X ∈ C2 \{0} tel que AX = λX. L’application u ∈ L(R 2 )↦→ MB(u)X ∈ C2 est linéaire donc continue ; par caractérisation des applications linéaires continues, on en déduit que la suite (AnX)n est encore bornée. Comme X≠0, il vient que (λn )n∈N est bornée, donc |λ|≤ 1.

Nous montrons ensuite les deux résultats suivants, qui répondent essentiellement à la question :

  • Si (fn )n converge vers un p 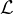∈L(R2), alors R2 = Ker(f -id) ⊕Im(f -id) et p est le projecteur sur Ker(f -id) parallèlement à Im(f -id). Dans ce cas - 1 n’est pas valeur propre de f.
  • La suite (fn)n converge si et seulement si - 1 n’est pas valeur propre de f.

Le point (b) est très général et n’utilise que le fait que f est un endomorphisme d’un espace vectoriel de dimension finie. Supposons en effet que (fn)n converge vers un p 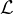∈L(R2). La composition des endomorphismes de R2 est bilinéaire donc continue. En passant à la limite dans les relations

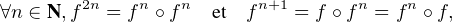
∀n ∈ N,f2n = fn • fn et fn+1 = f • fn = fn •f,
on en déduit p2 = p et f • p = p • f = p. La première relation montre que p est un projecteur, la deuxième donne les inclusions Im(f - id) ⊂ Ker(p) et Imp ⊂ Ker(f - id).

Soit x un vecteur propre de f associé à une valeur propre λ. Alors fn(x) = λnx pour tout n ∈ N. Comme l’évaluation en x est continue car linéaire, et on en déduit que (λn)n converge vers un réel α tel que p(x) = αx. En particulier λ ∈]- 1,1] d’après (a). Si en outre λ = 1 alors α = 1. Ce dernier point montre que Ker(f - id) ⊂ Imp.

On a établi Ker (f - id) = Imp. En appliquant le théorème du rang à f - id et p, il vient rg(f - id ) = dimKer(p), d’où Im(f -id) = Kerp car une des inclusions est déjà connue. Le point (b) est donc établi.

Terminons par le point (c). Le sens direct a déjà été établi en (b). Supposons que - 1 ne soit pas valeur propre de f. Notons que χf est de degré 2 à coefficients réels, donc soit il est scindé sur R, soit il est scindé à racines simples sur C \ R, conjuguées l’une de l’autre.

  • Supposons d’abord χf scindé sur C, à racines simples α,β dans Do(0,1)∪{1}. Alors A est diagonalisable dans M2(C). Cela fournit P ∈ GL2(C) tel que A = PDP-1 où D = Diag(α,β). On a donc ∀n ∈ N,A = PDnP-1. Comme les suites (αn)n et (βn )n convergent, la suite (Dn)n = (Diag(αn,βn))n converge. Par continuité du produit matriciel, il vient que (An)n converge. Enfin, l’application qui, à une matrice M de M2 (R), associe l’endomorphisme X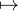↦→MX de R2, est continue car linéaire. On conclut à la convergence de (fn)n.
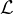  • Supposons que χf ait une racine double λ, nécessairement réelle. Alors λ ∈]- 1,1] vu le point (a). En trigonalisant f, on obtient f = λid+v avec v ∈ L(R2) nilpotent (et donc v2 = 0). Par la formule du binôme ( id et v commutent), il vient fn = λn idR2 + nλn-1v pour tout n ∈ N*. Si |λ| < 1, cela suffit à voir que (fn)n converge vers 0. Si λ = 1 alors, (fn)n étant bornée, on doit avoir v = 0 soit f = id, mais cela contredit alors le fait que f(C)≠C.

Vu ce qui précède, il ne reste plus qu’à étudier le cas où χf est scindé à racines simples non réelles α et α , avec |α| = 1. On suppose donc que l’on est dans cette situation. Nous montrons alors que idest adhérent à {fn∣n ∈ N*}. Prenons en effet une matrice P ∈ GL2(C) telle que PDP-1 = A où D := Diag(α,α). La suite (αn)n est à valeurs dans le compact U (fermé borné d’un espace de dimension finie) donc il existe une extraction φ telle que (αφ(n))n converge dans U. Puis (αφ(n+1)-φ(n))n converge vers 1, et, par continuité du produit matriciel, (Aφ(n+1)-φ(n))n converge vers I2. Ainsi (fφ(n+1)-φ(n))n converge vers id.

Or, on peut choisir un point x ∈ C \ f(C). L’évaluation en x étant continue car linéaire, la suite (fφ(n+1)-φ(n) (x))n converge vers x. Or, C étant stable par f, on a fk(x) ∈ f(C) pour tout k ∈ N * , et x serait donc adhérent à f(C). C’est absurde car, C étant compact et f continue, f(C) est compact donc fermé dans R2 !

Le point (c) est finalement établi, ce qui achève l’étude.


[Liste des corrigés]


[ < ]