
 2(R). Montrer que la classe de similitude de M est connexe par arcs si et
seulement si M est diagonalisable.
2(R). Montrer que la classe de similitude de M est connexe par arcs si et
seulement si M est diagonalisable.
Solution d’après Nguyên Hai Châu
On rappelle que l’ensemble GL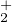 (R) = {M
(R) = {M 
 2(R)∣detM > 0} est connexe par arcs (c’est
une conséquence de l’algorithme du pivot de Gauss).
2(R)∣detM > 0} est connexe par arcs (c’est
une conséquence de l’algorithme du pivot de Gauss).
Soit M 
 2 (R ) une matrice diagonalisable. Notons D une matrice diagonale semblable à M. La
classe de similitude C de M est celle de D, elle est la réunion des ensembles
2 (R ) une matrice diagonalisable. Notons D une matrice diagonale semblable à M. La
classe de similitude C de M est celle de D, elle est la réunion des ensembles
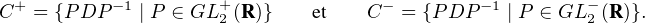
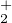 par la fonction continue
P
par la fonction continue
P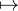 PDP-1 ). Par ailleurs on a C+ = C- en effet la matrice diagonale E = diag(1,-1) commute
avec D, donc pour toute matrice inversible P , on a PDP-1 = P(EDE-1)P-1 = QEQ-1 avec
Q = PE et il est clair que P
PDP-1 ). Par ailleurs on a C+ = C- en effet la matrice diagonale E = diag(1,-1) commute
avec D, donc pour toute matrice inversible P , on a PDP-1 = P(EDE-1)P-1 = QEQ-1 avec
Q = PE et il est clair que P  GL
GL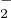 (R)⇐⇒Q
(R)⇐⇒Q  GL
GL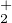 (R). Ainsi C = C+ est connexe par
arcs.
(R). Ainsi C = C+ est connexe par
arcs.
Réciproquement, supposons C connexe par arcs. Si l’on conjugue M = 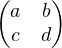 par
par  , on
obtient Mʹ =
, on
obtient Mʹ = 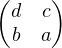 . La fonction f :
. La fonction f :  2(R) → R, A
2(R) → R, A a12 - a21 est continue et on a
f(M) = -f(Mʹ). Comme C est connexe par arcs, il existe N
a12 - a21 est continue et on a
f(M) = -f(Mʹ). Comme C est connexe par arcs, il existe N  C tel que f(N) = 0. Cela signifie
que N est symétrique réelle, donc diagonalisable. La matrice M, semblable à N, est elle aussi
diagonalisable.
C tel que f(N) = 0. Cela signifie
que N est symétrique réelle, donc diagonalisable. La matrice M, semblable à N, est elle aussi
diagonalisable.
[Liste des corrigés]

