a) Montrer que pour tout u  GL(E) il existe un unique polynôme Iu
GL(E) il existe un unique polynôme Iu  C[X] de degré
minimal tel que u-1 = Iu(u), et justifier que deg Iu < n.
C[X] de degré
minimal tel que u-1 = Iu(u), et justifier que deg Iu < n.
b) Étudier la continuité de u  GL(E)
GL(E)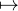 Iu
Iu  Cn-1[X].
Cn-1[X].
a) Soient u  GL(E) et πu = Xs + as-1Xs-1 +
GL(E) et πu = Xs + as-1Xs-1 +  + a0 le polynôme minimal de u. Comme u
est inversible, 0 n’est racine de πu et a0 ⁄= 0. On a donc
+ a0 le polynôme minimal de u. Comme u
est inversible, 0 n’est racine de πu et a0 ⁄= 0. On a donc
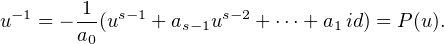
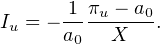
b) Rappelons qu’un endomorphisme u 
 (E) est dit cyclique s’il existe a
(E) est dit cyclique s’il existe a  E tel que (a,u(a),…,
un-1 (a)) soit libre et que u cyclique équivaut à πu = χu ou encore à deg(πu) = deg(χu) (où χu
est le polynôme caractéristique de u). Si, donc u est cyclique alors πu = χu, a0 = χu(0) = det(u),
d’où
E tel que (a,u(a),…,
un-1 (a)) soit libre et que u cyclique équivaut à πu = χu ou encore à deg(πu) = deg(χu) (où χu
est le polynôme caractéristique de u). Si, donc u est cyclique alors πu = χu, a0 = χu(0) = det(u),
d’où
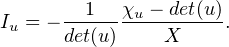
Comme l’ensemble des endomorphismes cycliques est ouvert (car si a  E est tel que
(a, u(a), … , un-1 (a)) soit libre alors (a,v(a),…,vn-1(a)) l’est aussi pour tout v
E est tel que
(a, u(a), … , un-1 (a)) soit libre alors (a,v(a),…,vn-1(a)) l’est aussi pour tout v 
 (E)
suffisamment proche de u) et u
(E)
suffisamment proche de u) et u χu est continue (les coefficients de χu sont des polynômes
en les coefficients de la matrice de u dans un base quelconque) ainsi que u
χu est continue (les coefficients de χu sont des polynômes
en les coefficients de la matrice de u dans un base quelconque) ainsi que u det(u),
l’application u
det(u),
l’application u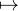 Iu est continue en tout point de l’ouvert des endomorphismes cycliques
inversibles.
Iu est continue en tout point de l’ouvert des endomorphismes cycliques
inversibles.
Supposons réciproquement I continue en u et considérons une suite vk d’endomorphisme admettant
n valeurs propres distinctes et convergeant vers u (l’existence d’une telle suite est classique).
Alors vk est cyclique et l’on a Ivk = -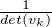
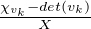 d’où, par passage à la limite,
Iu = -
d’où, par passage à la limite,
Iu = -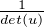
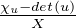 puis deg(πu) = n.
puis deg(πu) = n.
Finalement, I est continue en u si et seulement si u est cyclique.

