N* tels qu’existe A 
n(R) de polynôme minimal X3 + 2X + 2.
Même question dans n(Q).
Solution de Eric Pité
Que ce soit sur R ou Q, d’après le théorème de Cayley-Hamilton, on a nécessairement n ≥ 3.
De plus, la matrice A3 =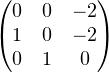 
admet 
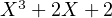pour polynôme caractéristique et
minimal.
Plaçons-nous sur n(
). Le polynôme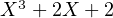 
possède une racine réelle (et une seule)
que l’on note a. Si n ≥ 4, la matrice A diagonale par blocs définie par
A = diag (A3 , 
n-3 fois)
admet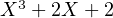 
pour polynôme minimal. Donc, pour tout n ≥ 3, il existe 
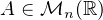de
polynôme minimal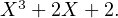 
Plaçons nous sur n(Q). Si n = 3m, avec m N*, alors la matrice A diagonale par blocs définie
par
A = diag (
m fois)
admet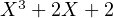 
pour polynôme minimal. Étudions la réciproque.
Soien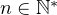t 
et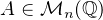 
de polynôme minimal 
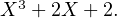Si le polynôme unitaire
![X3+2X+2∈Z[X ]](/numeros/RMS130-3/RMS130-31612x.png)
possède une racine dans Q alors elle est dans Z, or la seule racine
réelle a ≃ -0, 771 ⁄ Z. Alternativement, on peut remarquer qu’une racine entière doit
diviser 2 et que ± 1,±2 ne sont pas racines. Ainsi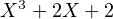 
est irréductible sur
Q[X].
Le polynôme caractéristique de A, χA Q[X], divise une puissance de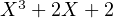 
. Ce dernier
étant irréductible sur Q[X], il existe m N* tel que χA = (X3 + 2X + 2)m. Donc
n = 3m.
[Liste des corrigés]