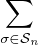249. Pour n ∈ N* et σ dans Sn, soit Pσ la matrice de permutation associée à σ. Pour n ∈ N, soit Tn = ∑ σ∈Sn det(In + Pσ).

a) Calculer 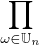∏ ω∈Un(1 + ω).

b) Pour n ∈ N * et σ dans Sn, calculer det(In + Pσ).

c) Montrer que, pour tout n ∈ N*, Tn+1 = 2Tn + n(n - 1)Tn-1.

d) Donner une formule simple pour Tn.

On complétera le calcul demandé par celui, un peu plus général, de l’espérance du polynôme caractéristique de Pσ où Sn est muni de la loi uniforme.

a) Le polynôme P = Xn - 1 se factorise en P = 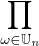∏ ω∈Un(X - ω) donc

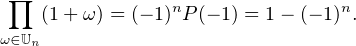
∏ n n (1+ ω) = (- 1) P(- 1) = 1 - (- 1) . ω∈Un

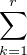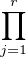b) Soient a1 , … , ar les longueurs des cycles de σ. On a r ∑ k=1ak = n. De plus σ est conjuguée dans Sn à toute permutation présentant les mêmes longueurs de cycles donc Pσ est semblable à la matrice diagonale par blocs Diag(M1,…,Mr) où Mj ∈Maj(R) est la matrice de la permutation circulaire (1, 2, … ,aj) dont le polynôme caractéristique est Xaj - 1. On en déduit donc det(In + Pσ ) = ∏r j=1(1 - (-1)aj).

c,d) Dans ce qui suit, pour tout ensemble A de cardinal n, on appellera polynôme caractéristique de la permutation σ de A le polynôme caractéristique de la matrice Pϕ-1•σ•ϕ où ϕ : [1,n]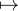↦→A est une bijection. Ce polynôme sera noté Cσ (avec la convention Cσ = 1 si n = 0). Il est indépendant du choix de ϕ car changer ϕ remplace Pϕ-1•σ•ϕ par une matrice qui lui est semblable.

Les questions c) et d) ont pour but de calculer l’espérance de (-1)nCσ(-1) où Sn est muni de la loi uniforme. Nous allons calculer plus généralement l’espérance Pn de Cσ pour A de cardinal n.

Notons dès à présent que, si σ stabilise une partie B de A, on a, en notant σ1 la restriction de σ à B et σ2 sa restriction à A \ B qui est aussi stable, Cσ = Cσ1Cσ2. Cela se voit en choisissant une bijection ϕ : [[1, n]]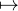↦→A telle que ϕ([[i,p]]) = A (où p = CardA).

Relation de récurrence Soit A de cardinal n + 1. Pour 1 ≤ k ≤ n + 1 notons Ek l’ensemble des σ ∈ Sn+1 telles que l’orbite de n + 1 est de longueur k. Pour σ ∈ Ek soit σ1 la permutation (circulaire) induite par σ sur l’orbite L de n + 1 et σ2 la permutation induite sur A \ L. On a Cσ1 = (Xk - 1) car σ1 est une permutation circulaire de k éléments, et donc, du fait que σ1 et σ2 sont indépendantes,

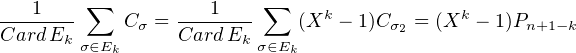
1 ∑ 1 ∑ --- Cσ = -------- (Xk - 1)Cσ2 = (Xk - 1)Pn+1-k CardEkσ∈Ek CardEk σ∈Ek

Par ailleurs CardEk = n.(n- 1)…(n-k + 2) × (n + 1 -k)! (on choisit l’image i de n + 1 puis celle de i etc..et on permute les n + 1 -k éléments restants) donc la probabilité que σ soit dans Ek est 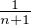1 n+1. On en déduit alors la formule (*)

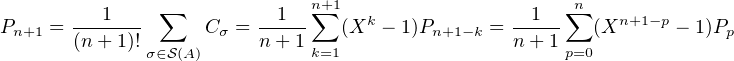
∑ n∑+1 ∑n Pn+1=1 Cσ = --1-- (Xk - 1)Pn+1-k = --1-- (Xn+1-p - 1)Pp (n+1)!σ∈S(A) n+ 1 k=1 n + 1p=0

On peut maintenant rapidement finir l’exercice.

En tenant compte de la relation Tn = n!(-1)nPn(-1)) il vient

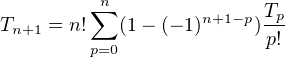
∑n n+1-p Tp Tn+1 = n! (1- (- 1) )p! p=0

pour n ≥ 1 en séparant les termes d’indice p = n et p = n - 1 (qui est nul) des autres on obtient

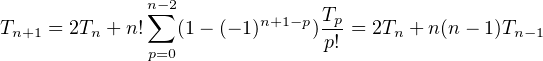
n∑-2 Tn+1= 2Tn + n! (1- (- 1)n+1-p)Tp = 2Tn + n(n - 1)Tn-1 p=0 p!

Un calcul direct donne T1 = 2,T2 = 4. La formule ci-dessus et une récurrence double conduisent alors à ∀n, Tn = 2.n!.

Complément De la formule (*) ci-dessus on déduit immédiatement que, pour n ≥ 1, l’espérance du polynôme caractéristique de σ ∈Sn est Pn = Xn - Xn-1.

En effet, c’est vrai pour n = 1 et si c’est vrai jusqu’à n alors, en tenant compte de P0 = 1, (*) donne

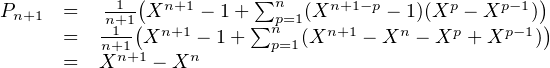
-1-( n+1 ∑n n+1-p p p-1) Pn+1 = n+11(Xn+1 - 1+ ∑np=1(Xn+1 -n1)(X p- X p-1)) = n+1n+X1 n- 1+ p=1(X - X - X + X ) = X - X

ce qui est remarquable car il s’agit là du polynôme caractéristique de l’espérance de Pσ .
[Liste des corrigés]


[ < ]