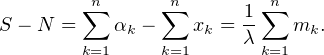< xn des nombres réels, λ
< xn des nombres réels, λ  R+* et,
pour x
R+* et,
pour x  R \ {xi ;1 ≤ i ≤ n}, f(x) =
R \ {xi ;1 ≤ i ≤ n}, f(x) = 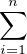
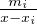 . Montrer que f-1([λ,+∞[) est une réunion
finie d’intervalles bornés. Calculer la somme des longueurs de ces intervalles.
. Montrer que f-1([λ,+∞[) est une réunion
finie d’intervalles bornés. Calculer la somme des longueurs de ces intervalles.
Solution de Ivan Gozard
L’application f est de classe 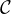 ∞ sur chaque intervalle inclus dans
∞ sur chaque intervalle inclus dans  \{xi,i
\{xi,i  [[1,n]]}, et
fʹ(x) = -
[[1,n]]}, et
fʹ(x) = -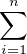
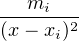 < 0. Donc f est strictement décroissante sur chacun de ces intervalles, et
son tableau de variation est :
< 0. Donc f est strictement décroissante sur chacun de ces intervalles, et
son tableau de variation est :

 [[1,n - 1]] (resp. pour k = n) il existe un unique αk
[[1,n - 1]] (resp. pour k = n) il existe un unique αk  ]xk,xk+1[ (resp.
αk
]xk,xk+1[ (resp.
αk  ]xn , +∞[) tel que f(αk) = λ. L’ensemble D = {x
]xn , +∞[) tel que f(αk) = λ. L’ensemble D = {x 
 ⁄ f(x) ≥ λ} est la réunion des n
intervalles bornés disjoints ]x1,α1],…,]xn-1,αn-1] et ]xn,αn]. La somme de leurs longueurs
est
⁄ f(x) ≥ λ} est la réunion des n
intervalles bornés disjoints ]x1,α1],…,]xn-1,αn-1] et ]xn,αn]. La somme de leurs longueurs
est
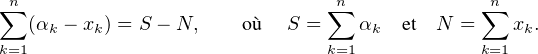
∙ Maintenant, faisons un peu d’algèbre. Par simple mise au même dénominateur, on obtient :
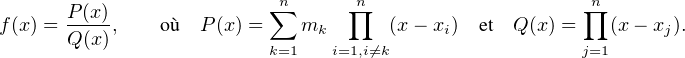
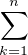 mk, le polynôme Q est unitaire de
degré n et l’on a
mk, le polynôme Q est unitaire de
degré n et l’on a
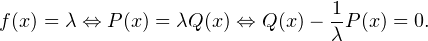
Le polynôme Q -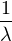 P est unitaire de degré n, et il a n racines, les αi,i
P est unitaire de degré n, et il a n racines, les αi,i  [[1,n]]. Donc
Q(x) -
[[1,n]]. Donc
Q(x) -  P(x) =
P(x) = 
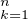 (x-αk). Par conséquent S =
(x-αk). Par conséquent S = 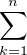 αk est l’opposé du coefficient de degré
n - 1 de Q(x) -
αk est l’opposé du coefficient de degré
n - 1 de Q(x) -  P(x). Or le coefficient de degré n - 1 de Q(x) =
P(x). Or le coefficient de degré n - 1 de Q(x) = 
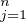 (x - xj) est
-
(x - xj) est
- 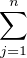 xj = -N, et P est de degré n - 1 et a pour coefficient dominant
xj = -N, et P est de degré n - 1 et a pour coefficient dominant 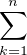 mk. Donc
S =
mk. Donc
S = 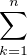 αk = N +
αk = N + 
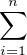 mk. La somme des longueurs des intervalles constituant D est
donc :
mk. La somme des longueurs des intervalles constituant D est
donc :