Solution synthétisant les propositions de Salim Alloun, Maxime Bourrigan, Christophe Jan, Moubinool Omarjee, Éric Pité, Marien Renaud et Colas Bardavid
À toute partie A de N, on attribue la fonction σA : N → N définie comme suit : pour
tout k  N, σA (2k) = 2k et σA(2k + 1) = 2k + 1 si k
N, σA (2k) = 2k et σA(2k + 1) = 2k + 1 si k  A, et σA(2k) = 2k + 1 et
σA (2k + 1) = 2k sinon ; elle vérifie évidemment σ
A, et σA(2k) = 2k + 1 et
σA (2k + 1) = 2k sinon ; elle vérifie évidemment σ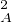 = idN et c’est donc une permutation de
N.
= idN et c’est donc une permutation de
N.
Notons que pour tout A ⊂ N, on retrouve A = {k  N : σA(2k) = 2k}, si bien que la fonction
A
N : σA(2k) = 2k}, si bien que la fonction
A 
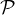 (N)
(N)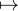 σA
σA  𝔖(N) est injective. Par suite, si 𝔖(N) était fini ou dénombrable alors
𝔖(N) est injective. Par suite, si 𝔖(N) était fini ou dénombrable alors 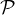 (N) le
serait également.
(N) le
serait également.
On conclut que 𝔖(N) est indénombrable puisque, classiquement, 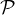 (N) est indénombrable. Ce
résultat dernier ne figurant pas explicitement au programme, redémontrons-le. Pour toute fonction
f : N →
(N) est indénombrable. Ce
résultat dernier ne figurant pas explicitement au programme, redémontrons-le. Pour toute fonction
f : N → 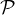 (N), l’ensemble A := {n
(N), l’ensemble A := {n  N : n ⁄
N : n ⁄ f(n)} est hors de l’image de f (en effet si c’était
l’image d’un entier k par f on aurait k
f(n)} est hors de l’image de f (en effet si c’était
l’image d’un entier k par f on aurait k  A si et seulement si k
A si et seulement si k  f(k) ce qui contredirait la
définition de A), si bien que f n’est pas surjective. Comme
f(k) ce qui contredirait la
définition de A), si bien que f n’est pas surjective. Comme 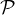 (N) est évidemment non vide, la
conclusion s’ensuit.
(N) est évidemment non vide, la
conclusion s’ensuit.
Solution d’après Rémi Morvan et Duncan Sussfeld, élèves de l’ENS Paris-Saclay
Il existe une bijection σ : N → Q ; la fonction φ  𝔖(N)
𝔖(N) σ • φ • σ-1
σ • φ • σ-1  𝔖(Q) est alors
clairement une bijection. Il suffit donc de montrer que 𝔖(Q) est indénombrable. Pour cela, il suffit
de construire une injection de R dans 𝔖(Q), l’indénombrabilité - connue - de R impliquant alors
celle de 𝔖(Q).
𝔖(Q) est alors
clairement une bijection. Il suffit donc de montrer que 𝔖(Q) est indénombrable. Pour cela, il suffit
de construire une injection de R dans 𝔖(Q), l’indénombrabilité - connue - de R impliquant alors
celle de 𝔖(Q).
Soit x un réel. Les ensembles Q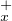 := {y
:= {y  Q : y ≥ x} et Q
Q : y ≥ x} et Q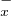 := {y
:= {y  Q : y < x} sont évidemment
infinis, donc dénombrables car ils sont inclus dans Q qui est dénombrable. Il existe donc une
bijection gx : Q
Q : y < x} sont évidemment
infinis, donc dénombrables car ils sont inclus dans Q qui est dénombrable. Il existe donc une
bijection gx : Q 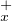 → Q
→ Q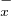 . On peut alors définir une permutation (involutive) fx : Q → Q par la
formule fx (y) = gx(y) si y
. On peut alors définir une permutation (involutive) fx : Q → Q par la
formule fx (y) = gx(y) si y  Q
Q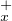 , et fx(y) = g
, et fx(y) = g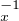 (y) sinon. On notera en particulier que
fx (y) < y si y
(y) sinon. On notera en particulier que
fx (y) < y si y  Q
Q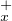 , et fx(y) > y sinon.
, et fx(y) > y sinon.
Montrons pour finir que x  R
R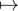 fx est injective. Soit a < b dans R. Par densité de Q dans R, il
existe un rationnel y dans
fx est injective. Soit a < b dans R. Par densité de Q dans R, il
existe un rationnel y dans ![]a,b[](/numeros/RMS130-3/RMS130-3306x.png) . Alors ga(y) < y et gb(y) > y, donc ga≠gb. Cela achève la
démonstration.
. Alors ga(y) < y et gb(y) > y, donc ga≠gb. Cela achève la
démonstration.

