235. Soit P un polynôme complexe non nul ayant au moins deux racines distinctes et tel que Pʹʹ divise P.

a) Montrer que P est à racines simples.

b) Montrer que les racines de P sont alignées.

Solution de Mohamed Houkari

a) Supposons que P admet une racine au moins double a ∈ C, dont on note α ≥ 2 la multiplicité. On écrit alors P = (X - a)αQ et Pʹʹ = (X - a)α-2R avec Q(a)≠0 et R(a)≠ 0.

Comme Pʹʹ |P, R divise (X -a)αQ. Comme R(a)≠0, alors R divise Q. Compte tenu de l’égalité deg(Q) = deg (R), on constate que Q et R sont associés. Notant n le degré de P , on a alors

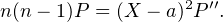
n (n - 1)P = (X - a)2Pʹʹ.

On écrit alors la formule de Taylor pour P et Pʹʹ en a :

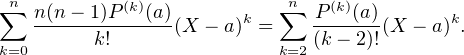
∑n n(n---1)P-(k)(a) k ∑n P-(k)(a)- k k! (X - a) = (k- 2)!(X - a) . k=0 k=2

L’identification donne 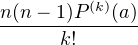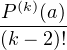n (n - 1)P(k)(a) ------k!------ = P(k)(a) (k---2)!- pour tout k ∈{2,…,n}, ce qui montre que

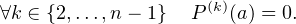
∀k ∈ {2,...,n- 1} P (k)(a) = 0.

Ainsi, a est racine d’ordre au moins n de P , d’où P = λ(X -a)n avec λ ∈ C. Ceci est interdit par les hypothèses, puisque P doit avoir au moins 2 racines distinctes.

En définitive, P n’admet que des racines simples.

b) C’est un résultat classique (théorème de Gauss-Lucas) que d’affirmer que les racines de Pʹ sont dans l’enveloppe convexe de celles de P . Démontrons-le. En notant a1,…,an les racines (simples, d’après la question précédente) de P , on a

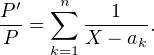
ʹ ∑n P--= ---1--. P k=1X - ak

Si β est une racine de Pʹ (qui n’est donc pas un des ak), on conjugue l’égalité ci-dessus, évaluée en β, et on obtient

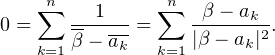
n n 0 = ∑ --1---= ∑ -β---ak-. k=1 β - ak k=1|β - ak|2

Ceci montre que β est dans l’enveloppe convexe des points a1,…,an.

Supposons que les racines de P ne sont pas alignées. L’enveloppe convexe des racines de P , qui est un polygone, n’est donc pas incluse dans une droite et compte trois sommets non alignés (les sommets de cette enveloppe convexe sont des racines de P ). Comme Pʹʹ|P et comme deg(Pʹʹ ) = deg (P) - 2, alors l’un de ces sommets est racine de Pʹʹ. Or, les racines de Pʹ sont toutes distinctes de celles de P , donc l’enveloppe convexe des racines de Pʹ ne contient aucun des sommets de l’enveloppe convexe de celles de P . Il y a donc une racine de Pʹʹ qui se situe hors de l’enveloppe convexe de celles de Pʹ. Or, les racines de Pʹʹ doivent être comprises dans l’enveloppe convexe des racines de Pʹ, d’après le théorème de Gauss-Lucas : contradiction.

Finalement, les racines de P sont donc alignées.

Dans la question b) , nous nous sommes appuyés sur des considérations géométriques simples sur les polygones convexes P. Un sommet d’un tel polygone est un point extrémal de P, c’est-à-dire un point x tel que P -{x}soit encore convexe.
[Liste des corrigés]


[ < ]