 G, on note x la classe de conjugaison de x :
G, on note x la classe de conjugaison de x :
x= {gxg-1 ; g  G} ; on dit que x est ambivalent si x-1
G} ; on dit que x est ambivalent si x-1  x.
x.
a) Montrer que si une classe de conjugaison contient un élément ambivalent, alors tous ses éléments le sont.
b) Pour x  G, soit ρ(x) le nombre de g
G, soit ρ(x) le nombre de g  G tels que g2 = x. Montrer que
G tels que g2 = x. Montrer que 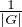
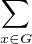 ρ(x)2 est le
nombre de classes de conjugaison ambivalentes de G.
ρ(x)2 est le
nombre de classes de conjugaison ambivalentes de G.
a) Soit γ une classe de conjugaison qui contient un élément ambivalent u. Soit h  G tel que
u = hu-1 h-1 . Soit v
G tel que
u = hu-1 h-1 . Soit v  γ et posons v = lul-1. On vérifie que v =
γ et posons v = lul-1. On vérifie que v = 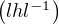 v-1
v-1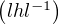 -1, ainsi v
est ambivalent.
-1, ainsi v
est ambivalent.
b) Notons Γ l’ensemble des classes ambivalentes. Alors, en désignant par δ le symbole de Kronecker,
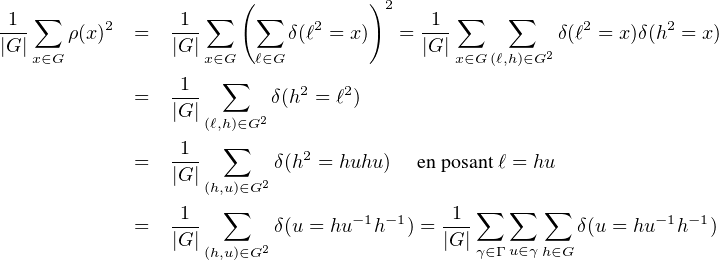
 Γ et u
Γ et u  γ. Considérons l’application ϕ : G → γ, h
γ. Considérons l’application ϕ : G → γ, h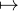 hu-1h-1. L’application ϕ est
surjective et on vérifie aisément que chaque pré-image a le même cardinal
hu-1h-1. L’application ϕ est
surjective et on vérifie aisément que chaque pré-image a le même cardinal
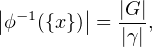
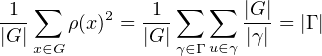
Reformulation. Soient X et Y deux variables aléatoires indépendantes suivant le loi uniforme sur G.
On a alors P(X2 = Y 2) = 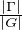 . En effet
. En effet
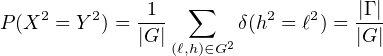
d’après le calcul précédent.

