 Z*× Z*× Z vérifie a ∧ b = ab ∧ p = 1, v
Z*× Z*× Z vérifie a ∧ b = ab ∧ p = 1, v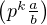 = k.
= k.
a) Pour (x, y)  Q2, montrer que v(xy) = v(x) + v(y),v(x + y) ≥ min(v(x),v(y)).
Q2, montrer que v(xy) = v(x) + v(y),v(x + y) ≥ min(v(x),v(y)).
b) Pour n  N * , montrer que v(n!) <
N * , montrer que v(n!) < 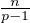 .
.
c) Soit P = 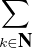 akXk
akXk  Q[X]. Pour i
Q[X]. Pour i  N, soit v(i)(P) = min{v(aj);j
N, soit v(i)(P) = min{v(aj);j  N,j ≥ i}. On fixe
m
N,j ≥ i}. On fixe
m  N , R = (X - m)P . Montrer que ∀i
N , R = (X - m)P . Montrer que ∀i  N,v(i+1)(R) ≥ v(i)(P).
N,v(i+1)(R) ≥ v(i)(P).
d) Soient (dn )n N
N  ZN et, pour n
ZN et, pour n  N, bn =
N, bn = 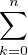 (n
k)
dkpk. Montrer que, si la suite (bn)n
(n
k)
dkpk. Montrer que, si la suite (bn)n N
s’annule une infinité de fois, elle est identiquement nulle.
N
s’annule une infinité de fois, elle est identiquement nulle.
a) Notons que si (a,b,k)  Z*× Z*× Z vérifie b ∧ p = 1 alors v
Z*× Z*× Z vérifie b ∧ p = 1 alors v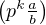 ≥ k.
≥ k.
Supposons x = pi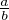 et y = pj
et y = pj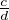 avec a ∧ b = c ∧ d = (abcd) ∧ p = 1. Alors
avec a ∧ b = c ∧ d = (abcd) ∧ p = 1. Alors
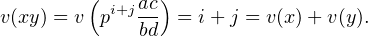
De plus, si i ≤ j, alors x + y = pi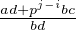 et on a (bd) ∧ p = 1 donc v(x + y) ≥ i.
et on a (bd) ∧ p = 1 donc v(x + y) ≥ i.
b) Nous utiliserons la formule de Legendre qui affirme que pour tout entier n  N* et tout nombre
premier p on a
N* et tout nombre
premier p on a
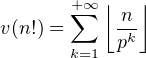
Preuve Pour 1 ≤ k ≤ N = 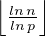 , le nombre des multiples de pk compris entre 1 et n est
ck =
, le nombre des multiples de pk compris entre 1 et n est
ck = 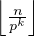 et celui des entiers multiples de pk mais pas de pk+1 est ck -ck+1 (où cN+1 = 0). On a
donc
et celui des entiers multiples de pk mais pas de pk+1 est ck -ck+1 (où cN+1 = 0). On a
donc
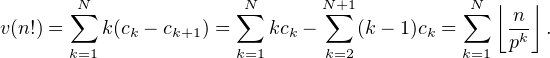
On peut alors majorer
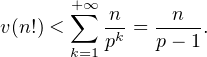
L’inégalité est stricte car 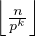 = 0 pour k assez grand.
= 0 pour k assez grand.
c) On a R = 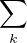 bkXk avec ∀k,bk = ak-1 - mak (avec a-1 = 0). Comme pour k ≥ i on a
v(aj ) ≥ v(i) (P) on déduit de a) que, pour tout k ≥ i, on a v(bk+1) ≥ v(i)(P) soit
v(i+1) (R) ≥ v(i) (P).
bkXk avec ∀k,bk = ak-1 - mak (avec a-1 = 0). Comme pour k ≥ i on a
v(aj ) ≥ v(i) (P) on déduit de a) que, pour tout k ≥ i, on a v(bk+1) ≥ v(i)(P) soit
v(i+1) (R) ≥ v(i) (P).
d) Considérons la base des polynômes de Hilbert définis par
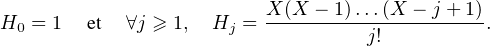
On peut alors écrire bn = 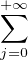 pjdjHj(n) puisque Hj(n) = 0 pour j ≥ n.
pjdjHj(n) puisque Hj(n) = 0 pour j ≥ n.
Supposons que bn s’annule pour les entiers n1 < n2 <  < nk et prenons N
< nk et prenons N  N quelconque tel
que N > nk . Soit enfin fN =
N quelconque tel
que N > nk . Soit enfin fN = 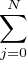 pjdjHj
pjdjHj  Q[X].
Q[X].
On a ainsi ∀n  {0,…,N},bn = fN(n).
{0,…,N},bn = fN(n).
En appliquant le c) avec le facteur P = 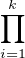 (X - ni) au polynôme fN on a
(X - ni) au polynôme fN on a
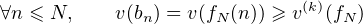
Or, pour j ≥ k, on a dj  Z donc
Z donc
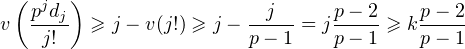
et donc le coefficient aj de Xj dans fN, qui est combinaison linéaire à coefficients
entiers des termes 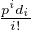 pour i ≥ j, a aussi une valuation p-adique supérieure à k
pour i ≥ j, a aussi une valuation p-adique supérieure à k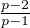 .
Finalement
.
Finalement
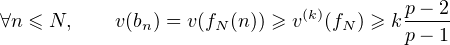
Ceci étant vrai pour tout N assez grand on a ∀n,v(f(n)) ≥ k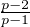 .
.
Comme (bn ) s’annule une infinité de fois ce qui précède s’applique pour tout k  N donc, du fait
que p ≥ 3, pour tout n
N donc, du fait
que p ≥ 3, pour tout n  N, v(bn) = +∞ i.e. bn = 0. On déduit alors par récurrence sur n que
bn = 0.
N, v(bn) = +∞ i.e. bn = 0. On déduit alors par récurrence sur n que
bn = 0.
Remarque Ce qui précède est issu de l’article
Le théorème de Skolem-Mahler-Lech par Nicolas Tosel, RMS 1 vol 116 Octobre 2005.
[Liste des corrigés]

