226. Soient a et b dans N*, (xn)n∈Z et (yn)n∈Z deux suites à valeurs dans un ensemble E, respectivement a-périodique et b-périodique. On suppose qu’il existe a + b - a ∧ b entiers relatifs consécutifs tels que xn = yn. Montrer que (xn)n∈Z = (yn)n∈Z.

Résolu par C. Jan, F. Capacès, E. Moulinier et L. Ponton.

On commence par le cas où a ∧ b = 1. Quitte à décaler les indices, on suppose que xn = yn pour tout n ∈ [[0, a + b - 2]]. Montrons que xa+b-1 = ya+b-1. L’idée : dans l’ensemble A = [[0, a + b - 1]], on part de l’indice i0 = a + b - 1 et on se déplace en retranchant des a et en ajoutant des b successivement jusqu’à retomber sur i0. Définissons la fonction f : A → A par

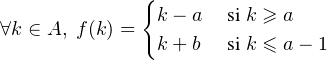
{k - a sik ≥ a ∀k ∈ A, f(k ) = k + b sik ≤ a - 1
(dans le deuxième cas, on a bien k + b ≤ a + b - 1 donc f(k) ∈ A). On vérifie facilement que f est bijective, de bijection réciproque définie par f-1(k) = k + a si k ≤ b - 1, f-1(k) = k - b si k ≥ b.

On définit alors une suite d’indices : i0 = a + b- 1 et, pour tout n ∈ N, in+1 = f(in). Comme f est une permutation, elle est d’ordre fini, donc il existe un plus petit p ∈ N* tel que i0 = ip. On a alors i1 , ..., ip-1 ∈ [[0,a + b- 2]]. Pour tout n tel que in,in+1 ∈ [[0,a + b- 2]], on a par hypothèse xin = yin et xin+1 = yin+1 ; de plus, si in ≥ a alors in+1 = in - a donc xin = xin+1, tandis que si in < a alors in+1 = in + b donc yin = yin+1. Dans les deux cas, on aboutit à xin = xin+1 = yin = yin+1. On a donc prouvé que xi1 = ... = xip-1 = yi1 = ... = yip-1.

Pour i0 = a + b - 1, on a i1 = i0 - a donc xa+b-1 = xi1. Pour ip = a + b - 1, on a ip-1 = f-1 (ip ) = ip - b donc yip-1 = ya+b-1. On obtient donc

xa+b-1 = xi1 = ⋅⋅⋅ = xip-1
= yi1 = ⋅⋅⋅ = yip-1 = ya+b-1.

Ainsi on a prouvé que xa+b-1 = ya+b-1. En réitérant le raisonnement (après avoir décalé tous les indices de 1), on montre ensuite que xa+b = ya+b, etc, par récurrence xn = yn pour tout n ≥ a + b - 1.

En raisonnant de même avec les suites (x-n)n∈Z et (y-n)n∈Z, on montre également que xn = yn pour tout n < 0. Finalement, les deux suites sont égales.

Dans le cas où d = a∧b > 1, on pose a = daʹ, b = dbʹ (avec aʹ∧bʹ = 1) et on raisonne avec les d paires de sous-suites ur = (xnd+r)n∈Z et vr = (ynd+r)n∈Z, 0 ≤ r < d. Pour chaque valeur de r, les suites ur et vr sont aʹ-périodique et bʹ-périodique respectivement, et coïncident sur une plage de aʹ + bʹ - 1 termes consécutifs. D’après le premier cas, elles sont égales. Ceci est valable pour tout r, donc (xn ) = (yn).
[Liste des corrigés]


[ < ]