∀(x, y)  R 2 , f(x + y) = f(x) + f(y).
R 2 , f(x + y) = f(x) + f(y).
a) Déterminer les fonctions continues vérifiant (*).
b) Si f vérifie (*) et si f n’est pas linéaire, montrer que le graphe de f est dense dans R2.
c) Déterminer les f vérifiant (*) et pour lesquelles il existe n > 1 tel que :
∀x > 0, f(xn ) = f(x)n.
Solution de François Capacès
a) Soit f vérifiant (*). En spécifiant x = y = 0, on a f(0) = 2f(0) soit f(0) = 0. En spécifiant
y = -x, on a f(-x) = -f(x). Une récurrence donne f(nx) = nf(x) pour tout n  N et pour tout
x
N et pour tout
x  R . On en déduit
R . On en déduit
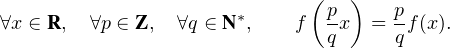
En particulier ∀r  Q,f(r) = αr en posant α = f(1).
Q,f(r) = αr en posant α = f(1).
Supposons f continue sur R. Alors x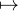 f(x) - f(1)x s’annule sur Q qui est dense dans R, et est
donc nulle sur R . Ainsi f est linéaire.
f(x) - f(1)x s’annule sur Q qui est dense dans R, et est
donc nulle sur R . Ainsi f est linéaire.
b) Puisque f n’est pas linéaire, il existe x,xʹ R* tels que
R* tels que 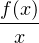 ≠
≠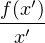 . Les vecteurs
u = (x, f(x)) et uʹ = (xʹ,f(xʹ)) forment une base de R2. Le graphe de f contient Qu + Quʹ donc
est dense dans R 2 .
. Les vecteurs
u = (x, f(x)) et uʹ = (xʹ,f(xʹ)) forment une base de R2. Le graphe de f contient Qu + Quʹ donc
est dense dans R 2 .
c) On suppose que f vérifie (*) et qu’il existe n ≥ 2 tel que (**) : ∀x > 0, f(xn) = f(x)n.
Les applications linéaires vérifiant (**) sont x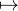 0, x
0, x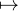 x et également, pour n impair,
x
x et également, pour n impair,
x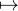 - x.
- x.
Si n est pair, alors ∀x > 0,f(x) = f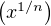 n est positif ou nul. Donc (1,-1) n’appartient pas à
l’adhérence du graphe de f, donc f est linéaire d’après b) .
n est positif ou nul. Donc (1,-1) n’appartient pas à
l’adhérence du graphe de f, donc f est linéaire d’après b) .
Si n est impair alors, en utilisant la Q-linéarité de f on a, pour x > 0 et t  Q+*,
Q+*,
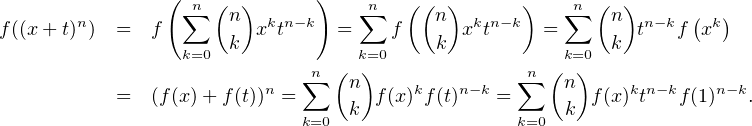
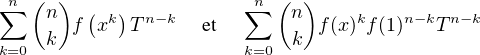
coïncident sur Q +*. Ces deux polynômes ont les mêmes coefficients. En particulier pour
k = n - 1 ≥ 2, on a nf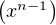 = nf(x)n-1f(1) et ce pour tout x > 0. Comme n- 1 est pair, on a
f
= nf(x)n-1f(1) et ce pour tout x > 0. Comme n- 1 est pair, on a
f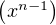 du signe de f(1) et de nouveau le graphe de f ne saurait être dense dans R2. Donc f est
linéaire.
du signe de f(1) et de nouveau le graphe de f ne saurait être dense dans R2. Donc f est
linéaire.
[Liste des corrigés]

