203. Soit V un hyperplan de M2(R) dont tous les éléments sont diagonalisables dans R .

a) Montrer que I2 ∈ V .

b) Donner un exemple de tel hyperplan V .

c) Montrer qu’il existe P ∈ GL2(R) telle que P-1V P contienne toutes les matrices diagonales.

d) Montrer qu’il existe Q ∈ GL2(R) telle que Q-1V Q = S2(R).

a) Considérons l’espace F des matrices de la forme 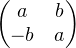( ) a b - b a . Une matrice de F est diagonalisable si et seulement si b = 0. Or par la formule de Grassman, on a dimV ∩F ≥ 1, donc il existe une matrice scalaire non nulle dans V , et ainsi I2 ∈ V .

b) On pense naturellement à S2(R), mais comme on le verra sur les questions suivantes, tout sous-espace conjugué à S2(R), de la forme QS2(R)Q-1 convient aussi.

c) Soit M dans V \V ect(I2). Alors M est diagonalisable et ses deux valeurs propres sont forcément distinctes. Ainsi il existe P telle que P-1MP = D := 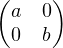(a 0) 0 b avec a≠b. Alors P-1 V P contient V ect(I2,D) qui est l’espace des matrices diagonales (car I2 et D sont libres dans cet espace qui est de dimension 2).

d) Munissons M2(R) du produit scalaire canonique ⟨A,B⟩ = trA⊤B, et soit A une matrice qui dirige V ⊥ . La théorie de la réduction des matrices réelles 2 × 2 nous apprend qu’il existe Q inversible, tel que A = P-1BP , où B est l’une des matrices

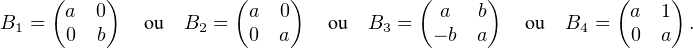
() ( ) ( ) ( ) B1=a0 ou B2 = a 0 ou B3 = a b ou B4 = a 1 . 0b 0 a - b a 0 a
En notant Q la transposée de P on a la chaîne d’équivalences :
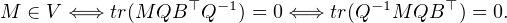
⊤ -1 -1 ⊤ M∈ V ⇐ ⇒ tr(M QB Q ) = 0 ⇐ ⇒ tr(Q M QB ) = 0.
Ainsi Q-1 V Q est l’orthogonal de B ; et Q-1V Q est constitué uniquement de matrices diagonalisables. Ceci interdit les cas de B1,B2 et B4 qui sont tous les trois orthogonaux à (0 0) 1 0 . De plus B est orthogonal à Q-1 I2Q = I2, donc B est de la forme B3 avec a = 0, ainsi il existe b non nul tel que
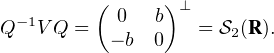
-1 ( 0 b)⊥ Q VQ = - b 0 = S2(R).

[Liste des corrigés]

[ < ]