La probabilité cherchée est 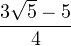 = 0.427050983125….
= 0.427050983125….
La solution d’Hervé Carrieu part sur la même idée que celle de Julien Bureaux.
La solution alternative proposée par la RMS ne donne pas directement la valeur exacte de cette probabilité. Elle sera complétée par la note finale.
Solution de Julien Bureaux
Considérons une suite infinie de lancers de la pièce, mutuellement indépendants.
Posons S0 = 0 puis, pour tout entier n > 0, notons Sn la différence entre le nombre de piles et le double du nombre de faces parmi les n premiers lancers. Les variables aléatoires Xn = Sn -Sn-1 sont mutuellement indépendantes et suivent la loi uniforme sur {1,-2}. L’exercice demande de calculer la probabilité p définie par :
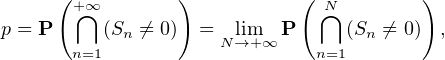
le passage à la limite étant justifié par continuité décroissante de P.
On introduit dans ce but, pour tout x de Z, la probabilité u(x) que la suite S n’atteigne jamais la valeur x :
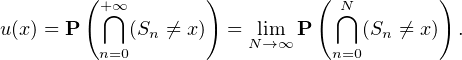
Puisque S0 = 0, on a trivialement u(0) = 0. De plus, on va exprimer p à l’aide de u en
distinguant les deux valeurs possibles de X1. Pour tout n de N, notons 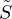 n la variable aléatoire
Sn+1 - X1 = X2 +
n la variable aléatoire
Sn+1 - X1 = X2 +  + Xn+1. En observant que les (Xi)i
+ Xn+1. En observant que les (Xi)i N* sont indépendantes et de même
loi, on obtient pour tout N
N* sont indépendantes et de même
loi, on obtient pour tout N  N* :
N* :
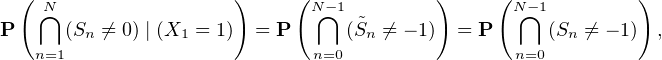
car on dispose d’une même fonction φ telle que (S0,…,SN-1) = φ(X1,…,XN-1) et
( 0 , … ,
0 , … ,  N-1 ) = φ(X2,…,XN). Pareillement :
N-1 ) = φ(X2,…,XN). Pareillement :
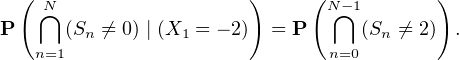
La formule des probabilités totales conduit alors, lorsque N →∞, à la relation :
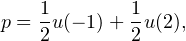
et le même raisonnement permet d’établir les relations de récurrence suivantes :
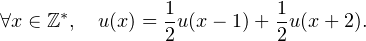
Les suites (u(x))x≥0 et (u(x))x≤1 sont donc récurrentes linéaires d’ordre7 trois, de même équation caractéristique t3 - 2t + 1 = 0, qui admet trois racines distinctes :
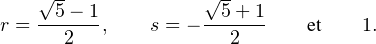
Il existe donc des réels α,β,γ tels que :
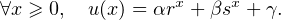
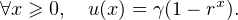
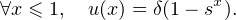
D’après ce qui précède, ceci détermine aussi la valeur de δ et donc toute la fonction u. Calculs faits, on obtient u(2) = r et u(-1) = 2r - 1, d’où finalement :
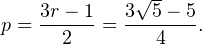
Démontrons maintenant le lemme. Soient des entiers x ≥ 0 et n ≥ 0. On va simplement majorer P(Sn = x) par P(Sn ≥ x) et utiliser l’inégalité de Markov suivante :
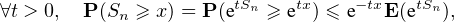
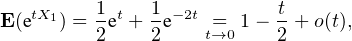
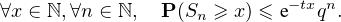
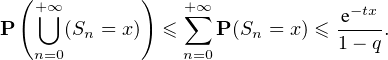
Remarque au sujet du lemme. Ce résultat est en fait immédiat lorsqu’on connaît la loi forte des grands nombres (hors programme) qui établit ici la convergence presque sûre :
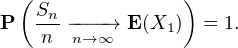
Puisque E(X1 ) < 0, ceci implique que, presque sûrement, la suite S diverge vers -∞ et est donc majorée. Or, par continuité croissante,
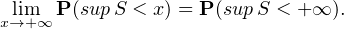
On conclut alors en remarquant que P(supS < x) ≤ u(x) pour tout x ≥ 1.
Solution alternative proposée par la RMS
On suppose les résultats des lancers indépendants.
Notons An l’événement : ≪ Au bout de 3n lancers, il y a 2n Pile et n Face ≫ainsi que Ak,n l’événement : ≪ Entre les lancers d’indice k + 1 à n, il y a 2n Pile et n Face ≫.
Pour n > 0 on note Bn l’événement An \ (A0 ∪ A1 ∪ ∪ An-1), c’est-à-dire l’événement
≪pour la première fois, au bout de 3n lancers, il y a 2n Pile et n Face ≫.
∪ An-1), c’est-à-dire l’événement
≪pour la première fois, au bout de 3n lancers, il y a 2n Pile et n Face ≫.
Notons pour n ≥ 0, pn la probabilité de An, qui est aussi celle de Ak,k+n et, pour n ≥ 1, qn la
probabilité de Bn .
On a p0 = 1 ; pour n > 0, l’événement An se décompose en réunion disjointe :
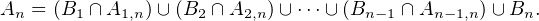
L’indépendance des lancers permet d’affirmer :
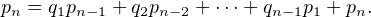
Or pour tout n :
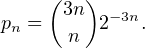
Notons P (resp. Q) la fonction génératrice de (pn) (resp. (qn)), soit :
P(x) = 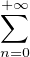 pnxn ; Q(x) =
pnxn ; Q(x) = 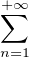 qnxn.
qnxn.
On a : lim (pn ⁄pn-1) = 27⁄32 < 1. Donc la série entière P admet R = 32⁄27 pour rayon de
convergence. Comme 0 ≤ qn ≤ pn, la série entière Q a un rayon de convergence au moins égal à
R.
On a d’après la relation de récurrence : P(x) = 1 + P(x)Q(x) puis Q(x) = 1 -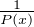 .
.
L’événement dont on cherche la probabilité est le complémentaire de la réunion disjointe infinie des
Bn . Donc la probabilité cherchée est 1 - Q(1) = 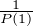 , soit
, soit
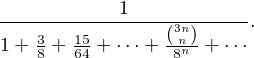
La fonction génératrice P s’exprime à l’aide des fonctions usuelles.
Considérons f : t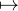 3sin
3sin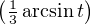 . Notons f(t) =
. Notons f(t) = 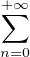 cnt2n+1 son développement en série
entière, justifié par la méthode de l’équation différentielle.
cnt2n+1 son développement en série
entière, justifié par la méthode de l’équation différentielle.
La fonction f est l’unique solution de 9(1 -t2)yʹʹ- 9tyʹ + y = 0 telle que y(0) = 0 et yʹ(0) = 1.
On en déduit cn = 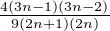 cn-1. Avec c0 = 1 il vient :
cn-1. Avec c0 = 1 il vient :
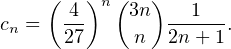
On en déduit pour |t| < 1 : 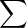
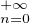
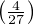 n(3n
n )
n(3n
n )
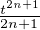 = 3sin
= 3sin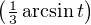 , et par dérivation :
, et par dérivation :
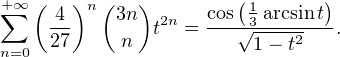
Ainsi
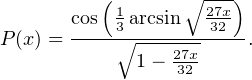
Et maintenant calculons u = P(1), l’inverse de la probabilité cherchée. On a u = 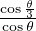 où
θ = arcsin
où
θ = arcsin 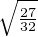 . Ainsi cosθ =
. Ainsi cosθ = 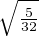 = 4cos3
= 4cos3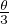 - 3cos
- 3cos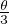 . Ces relations aboutissent
à :
. Ces relations aboutissent
à :
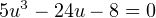
Le polynôme 5X3 - 24X - 8 a une racine ≪évidente ≫ : - 2. Les deux autres racines sont
1 ± 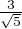 . La seule des racines strictement supérieure à 1 est u = 1 +
. La seule des racines strictement supérieure à 1 est u = 1 + 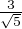 . C’est bien le résultat
voulu.
. C’est bien le résultat
voulu.
[Liste des corrigés]

