 [[1, k - 1]] tel que k - i soit pair, les lancers aux instants k et i aient donné face, et les
lancers à tous les instants strictement compris entre k et i aient donné pile. Montrer que T est
d’espérance finie, et calculer son espérance.
[[1, k - 1]] tel que k - i soit pair, les lancers aux instants k et i aient donné face, et les
lancers à tous les instants strictement compris entre k et i aient donné pile. Montrer que T est
d’espérance finie, et calculer son espérance.
Nous noterons P et F pour pile et face. On étudie le temps d’attente T d’un motif constitué de F, suivi d’un nombre impair de P , suivi de F , que nous noterons symboliquement FP2j+1 F.
Après n lancers de la pièce, il y a quatre états possibles :
- état 1 : on n’a pas encore obtenu de F ;
- état 2 : le motif n’est pas encore apparu mais les n premiers lancers se terminent par un F ou par un F suivi d’un nombre pair de P ;
- état 3 : le motif n’est pas encore apparu mais les n premiers lancers se terminent par un F suivi d’un nombre impair de P ;
- état 4 : le motif est apparu.
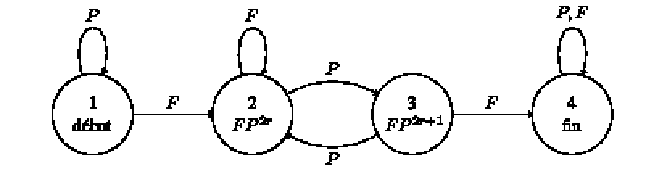
Ces 4 états forment une chaîne de Markov, représentée par le graphe ci-dessus (un informaticien
parlerait d’automate déterministe). Pour tout n  N*, on note Xn
N*, on note Xn  [[1,4]] la variable aléatoire
donnant l’état du système à l’issue des n premiers lancers. On pose X0 = 1.
[[1,4]] la variable aléatoire
donnant l’état du système à l’issue des n premiers lancers. On pose X0 = 1.
Les probabilités de transition pi,j = P(Xn+1 = j∣Xn = i) sont données par la matrice stochastique
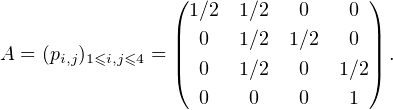
 P(Xn = 1), P(Xn = 2), P(Xn = 3), P(Xn = 4)
P(Xn = 1), P(Xn = 2), P(Xn = 3), P(Xn = 4) le vecteur ligne de R4 donnant la
loi de Xn . Alors on a μn+1 = μnA pour tout n
le vecteur ligne de R4 donnant la
loi de Xn . Alors on a μn+1 = μnA pour tout n  N (c’est la traduction de la formule des
probabilités totales : P(Xn+1 = j) =
N (c’est la traduction de la formule des
probabilités totales : P(Xn+1 = j) =  P(Xn = i)P(Xn+1 = j∣Xn = i)).
P(Xn = i)P(Xn+1 = j∣Xn = i)).
On a E(T) = 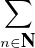 P(T > n)
P(T > n)  [0,+∞]. La suite d’événements ([Xn = 4])n
[0,+∞]. La suite d’événements ([Xn = 4])n N est croissante (car
l’état 4 est absorbant), donc on a :
N est croissante (car
l’état 4 est absorbant), donc on a :
![n⋂
[T > n] = [Xm ⁄= 4] = [Xn ⁄= 4]
m=1](/numeros/RMS130-3/RMS130-31292x.png)
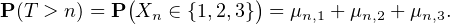
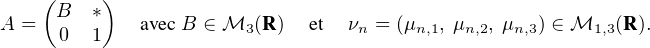
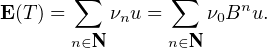
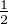 et
et 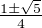 . Elles sont toutes de module < 1.
On en déduit que B est diagonalisable et que la série de terme général Bn est convergente, de
somme (I3 - B)-1. On calcule cette matrice et on conclut que
. Elles sont toutes de module < 1.
On en déduit que B est diagonalisable et que la série de terme général Bn est convergente, de
somme (I3 - B)-1. On calcule cette matrice et on conclut que
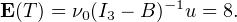
[Liste des corrigés]

