b) On munit R n de sa structure euclidienne standard. Soit T une partie de la boule unité
fermée, et x un point de l’enveloppe convexe de T . Montrer que pour tout k  N* il existe une
liste (x1 , … , xk )
N* il existe une
liste (x1 , … , xk )  Tk telle que
Tk telle que  x -
x -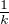
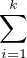 xi
xi ≤
≤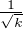 ⋅
⋅
Ind. Introduire des points deux à deux distincts y1,…,yp de T et des réels positifs λ1,…,λp tels
que x = 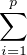 λiyi et 1 =
λiyi et 1 = 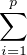 λi, puis considérer une variable aléatoire X telle que
P(X = yi ) = λi pour tout i
λi, puis considérer une variable aléatoire X telle que
P(X = yi ) = λi pour tout i  [[1,p]].
[[1,p]].
a) L’enveloppe convexe de A est constituée de toutes les combinaisons convexes de points de A,
c’est-à-dire de tous les vecteurs de la forme 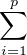 λixi où les λi sont positifs et de somme 1,
et les xi sont dans A. Pour montrer le résultat demandé, il suffit de vérifier que toute
combinaison convexe de p ≥ n + 2 vecteurs est encore combinaison convexe de p - 1
vecteurs.
λixi où les λi sont positifs et de somme 1,
et les xi sont dans A. Pour montrer le résultat demandé, il suffit de vérifier que toute
combinaison convexe de p ≥ n + 2 vecteurs est encore combinaison convexe de p - 1
vecteurs.
Supposons donc que x = 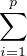 λixi où les xi sont dans A, les λi sont positifs et de somme 1 et
p ≥ n + 2. Si l’un des λi est nul, alors la question est résolue. Dans la suite, on supposera que tous
les λi sont strictement positifs.
λixi où les xi sont dans A, les λi sont positifs et de somme 1 et
p ≥ n + 2. Si l’un des λi est nul, alors la question est résolue. Dans la suite, on supposera que tous
les λi sont strictement positifs.
Soit 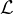 l’ensemble des p-uplets (μ1,μ2,…,μp) tels que
l’ensemble des p-uplets (μ1,μ2,…,μp) tels que 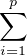 μixi = 0.
μixi = 0. 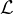 est un espace vectoriel,
noyau d’une application linéaire à valeurs dans Rn, donc la dimension de
est un espace vectoriel,
noyau d’une application linéaire à valeurs dans Rn, donc la dimension de 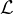 est supérieure ou égale
à p - n ≥ 2. Donc il existe un élément non nul de
est supérieure ou égale
à p - n ≥ 2. Donc il existe un élément non nul de 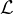 qui est de plus dans l’hyperplan
qui est de plus dans l’hyperplan 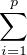 μi = 0. On
dispose donc d’une relation de liaison
μi = 0. On
dispose donc d’une relation de liaison
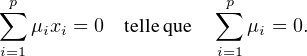
 R, on a x =
R, on a x = 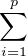 (λi + tμi)xi. Pour tout t
(λi + tμi)xi. Pour tout t  R on a
R on a 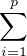 (λi + tμi) = 1 et pour t
assez petit, chaque λi + tμi reste strictement positif. On choisit alors un t ≪ limite ≫,
plus petit (en valeur absolue) pour lequel il existe i tel que λi + tμi = 0. Pour un tel t,
chaque λi + tμi est positif, l’un est nul. Donc x est combinaison convexe d’au plus p - 1
vecteurs.
(λi + tμi) = 1 et pour t
assez petit, chaque λi + tμi reste strictement positif. On choisit alors un t ≪ limite ≫,
plus petit (en valeur absolue) pour lequel il existe i tel que λi + tμi = 0. Pour un tel t,
chaque λi + tμi est positif, l’un est nul. Donc x est combinaison convexe d’au plus p - 1
vecteurs.
b) Commençons par le cas où k = 1. On écrit comme suggéré x = 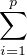 λiyi, et on considère donc
une variable aléatoire X définie sur un univers fini Ω, à valeurs dans {y1,…,yp} et dont la loi est
caractérisée par P(X = yi) = λi pour tout i
λiyi, et on considère donc
une variable aléatoire X définie sur un univers fini Ω, à valeurs dans {y1,…,yp} et dont la loi est
caractérisée par P(X = yi) = λi pour tout i  [[1,p]]. Alors x = E(X). Comme ∥X∥≤ 1, on a
alors
[[1,p]]. Alors x = E(X). Comme ∥X∥≤ 1, on a
alors
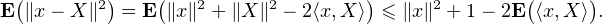
 ⟨x,X⟩
⟨x,X⟩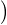 = ⟨x,E(X)⟩ = ∥x∥2, donc
= ⟨x,E(X)⟩ = ∥x∥2, donc
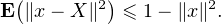
 Ω tel que ∥x - X(ω)∥2 ≤ 1 -∥x∥2 ≤ 1. C’est le résultat recherché pour
k = 1.
Ω tel que ∥x - X(ω)∥2 ≤ 1 -∥x∥2 ≤ 1. C’est le résultat recherché pour
k = 1.Pour k quelconque, on considère des variables aléatoires X1,…,Xk, mutuellement indépendantes et
de même loi que X ; on pose alors Y k = 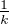
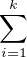 Xi. On a encore E(Y k) = x. En développant
comme ci-dessus, on obtient maintenant :
Xi. On a encore E(Y k) = x. En développant
comme ci-dessus, on obtient maintenant :
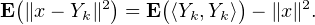
Or, E ⟨Y k,Y k⟩
⟨Y k,Y k⟩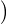 =
= 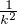
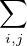 E
E ⟨Xi,Xj⟩
⟨Xi,Xj⟩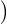 ; et E
; et E ⟨Xi,Xi⟩
⟨Xi,Xi⟩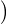 = E(∥Xi∥2) ≤ 1 tandis que, par
indépendance, E
= E(∥Xi∥2) ≤ 1 tandis que, par
indépendance, E ⟨Xi,Xj⟩
⟨Xi,Xj⟩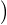 = ⟨E(Xi),E(Xj)⟩ = ∥x∥2 si i≠j. Il vient alors
= ⟨E(Xi),E(Xj)⟩ = ∥x∥2 si i≠j. Il vient alors
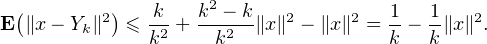
[Liste des corrigés]

