156. Soit (X_n )_nN une suite de variables aléatoires indépendantes suivant toutes la loi uniforme sur {-1,1}. Soit λ .

a) Montrer que, pour tout réel t, l’ensemble A_t = 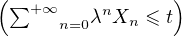est un événement.

b) Montrer que la fonction t R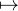P(A_t) est continue.

a) Soit (Ω, 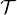, P) l’espace probabilisé sur lequel la suite (X_n) est définie.

On note, pour tout n N, Y _n = 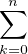λ^kX_k et Y = 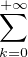λ^kX_k. Les Y _n sont des variables aléatoires discrètes, mais pas Y .

On a Y ≤ t si et seulement si : ∀ε > 0, ∃n₀ N, ∀n ≥ n₀, Y _n ≤ t + ε, ce qui se traduit par :

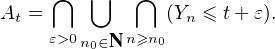
Dans cette expression, on peut remplacer ε > 0 par ε Q^+* sans que cela ne change A_t. Les ensembles (Y _n ≤ t + ε) sont des événements et la tribu 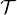est stable par union et intersection dénombrable, donc A_t est un événement.

b) Notons pour abréger F(t) = P(A_t) (c’est la fonction de répartition de Y ). L’idée est de conditionner par rapport à X₀ :

F(t)	= P(At∣X0 = -1)P(X0 = -1) + P(At∣X0 = 1)P(X0 = 1)
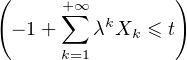	= P + P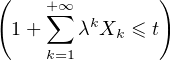

en effet les X_k pour k ≥ 1 sont indépendants de X₀,

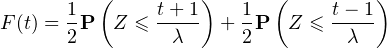
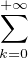où Z = λ^kX_k+1. Or les suites (X_k)_kN et (X_k+1)_kN sont deux suites de variables aléatoires indépendantes suivant toutes la même loi, donc Y et Z suivent la même loi : On obtient l’équation fonctionnelle La fonction F est croissante, bornée par 0 et 1. Elle possède des limites finies à gauche et à droite en tout point de R , que nous noterons F^-(t) = lim_t^-F et F⁺(t) = lim_t⁺F ; on pose aussi δ(t) = F⁺ (t) - F^-(t) (saut de F en t). Il est clair que les fonctions F^- et F⁺ vérifient la même équation fonctionnelle que F , et δ aussi.

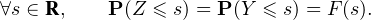
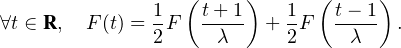
D’autre part δ est nulle sauf sur un ensemble fini ou dénombrable (car une fonction croissante a un nombre fini ou dénombrable de discontinuités) et on a S = 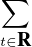δ(t) ≤ 1 (puisque 0 ≤ F ≤ 1, la hauteur cumulée des sauts ne peut dépasser 1). Il en résulte que δ, si elle n’est pas la fonction nulle, possède un maximum (prendre t R tel que δ(t) > 0, alors il ne peut y avoir qu’un nombre fini de points où δ dépasse la valeur δ(t), sinon S = +∞, donc il y a une valeur maximale). Soit t₀ un point où δ atteint son maximum. On a

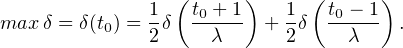
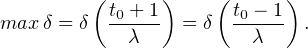
Il en résulte nécessairement que Posons, pour tout n N, t_n+1 = (t_n + 1)⁄λ, alors en itérant le raisonnement fait avec t₀, on montre que δ(t_n ) = max δ pour tout n. Si t₀≠(λ - 1)^-1, la suite (t_n) est injective. On voit alors que δ prend une infinité de fois une même valeur > 0, d’où S = +∞, c’est impossible. Si t₀ = (λ - 1)^-1 , on peut faire le même raisonnement avec la suite définie par t₀ʹ = t₀, tʹ_n+1 = (tʹ_n - 1)⁄λ (elle sera injective) et aboutir à la même contradiction. Conclusion : δ est la fonction nulle et F est continue sur R.
[Liste des corrigés]