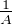
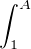 A1⁄x d x lorsque A tend vers + ∞.
A1⁄x d x lorsque A tend vers + ∞.
Voici deux solutions différentes.
Solution par Philippe Agnès
Notons, pour tout A > 1, f(A) = 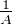
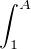 A1⁄x d x.
A1⁄x d x.
On va montrer que la limite de f(A) quand A tend vers + ∞ vaut 1.
Par le changement de variable u = 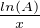 on obtient :
on obtient :
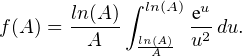
On écrit f(A) = g(A) + h(A) avec
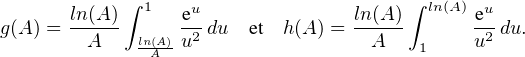
∙ tude de g(A) :
L’intégrale 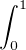
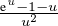 d u converge et
d u converge et
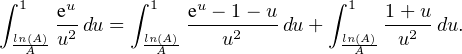
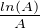 tend vers 0. Le deuxième vaut
tend vers 0. Le deuxième vaut
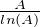 - 1 + ln
- 1 + ln 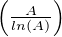 . Par croissance comparée ce terme équivaut à
. Par croissance comparée ce terme équivaut à 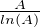 quand A tend vers
+ ∞.
quand A tend vers
+ ∞.
Ainsi 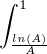
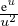 d u équivaut à
d u équivaut à 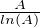 et donc g(A) tend vers 1 quand A tend vers + ∞.
et donc g(A) tend vers 1 quand A tend vers + ∞.
∙ tude de h(A) :
Par une intégration par parties :
![∫ln(A)eu [eu ]ln(A) ∫ ln(A)eu --A--- ∫ ln(A)-eu
1u2du = u2 + 2 1 u3 du = ln2(A) - e+ 2 1 u3 du.
1](/numeros/RMS130-3/RMS130-31215x.png)
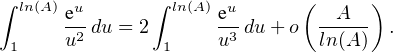
En étudiant la fonction φ : u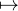
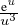 sur [1,+∞[, on constate que sur [1,ln(A)], elle est positive et
majorée par la plus grande des valeurs entre φ(1) et φ(ln(A)) =
sur [1,+∞[, on constate que sur [1,ln(A)], elle est positive et
majorée par la plus grande des valeurs entre φ(1) et φ(ln(A)) = 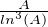 .
.
On en déduit que pour A assez grand :
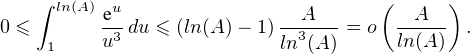
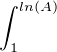
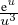 du = o
du = o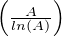 , puis
, puis 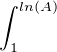
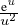 d u = o
d u = o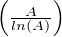 et h(A) = o(1) et donc h(A) tend vers
0 quand A tend vers + ∞.
et h(A) = o(1) et donc h(A) tend vers
0 quand A tend vers + ∞.
Ainsi la limite de 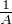
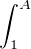 A1⁄x d x quand A tend vers + ∞ est 1.
A1⁄x d x quand A tend vers + ∞ est 1.
Solution par ric Pité
La fonction h : x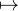 A1⁄x est définie et continue sur [1,+∞[ et est positive et décroissante.
A1⁄x est définie et continue sur [1,+∞[ et est positive et décroissante.
On a donc, pour A > 1 :
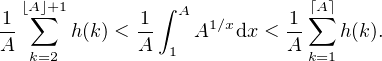
Le plus petit entier supérieur (resp. inférieur) ou égal à A est noté ⌈A⌉ (resp. ⌊A⌋).
Or lim x→+∞ h(x) = 1.
Ainsi, d’après le théorème de Cesàro
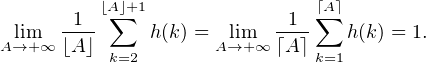
De plus lim A→+∞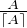 = limA→+∞
= limA→+∞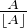 = 1, donc limA→+∞
= 1, donc limA→+∞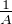
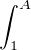 A1⁄xdx = 1.
A1⁄xdx = 1.
[Liste des corrigés]

