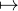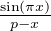Solution de Laurent Bonavero
La réponse est négative et nous en proposons deux démonstrations, dont la première est proposée par Laurent Bonavero.
Cela découle immédiatement du :
Lemme 1.Pour toute suite (ck)k  R
R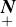 , il existe une fonction f : R → R, somme d’une
série entière, vérifiant : ∀k
, il existe une fonction f : R → R, somme d’une
série entière, vérifiant : ∀k  N, f(k) ≥ ck.
N, f(k) ≥ ck.
Preuve. Soit (nk )k N*
N*  NN*
strictement croissante telle que
NN*
strictement croissante telle que 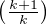 nk ≥ c
k+1. La série entière
c0 +
nk ≥ c
k+1. La série entière
c0 + 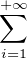
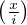 ni a un rayon de convergence infini puisque, pour tout r > 0, limi→+∞
ni a un rayon de convergence infini puisque, pour tout r > 0, limi→+∞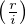 ni = 0, et
sa somme f vérifie f(0) ≥ c0 ainsi que, pour tout k
ni = 0, et
sa somme f vérifie f(0) ≥ c0 ainsi que, pour tout k  N,
N,
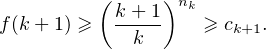
L’idée est similaire, mais on se propose de prouver un théorème d’interpolation plus précis :
Théorème 1.Pour toute suite (cn)n  RN, il existe une fonction f : R → R, somme d’une
série entière, vérifiant : ∀n
RN, il existe une fonction f : R → R, somme d’une
série entière, vérifiant : ∀n  N, f(n) = cn.
N, f(n) = cn.
Cet énoncé, et sa preuve, sont directement inspirés du théorème d’interpolation général qu’on peut lire dans le Rudin ([RU], théorème 15.13), lui-même corollaire du théorème de Mittag-Leffler. Nous aurons besoin du lemme suivant :
Preuve. On a
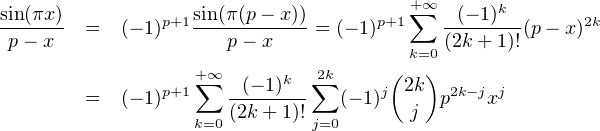
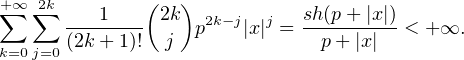
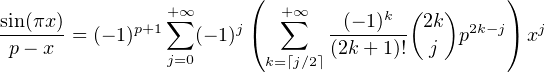
Preuve du théorème. Soit (cn)n N
N  RN. Choisissons, pour chaque n
RN. Choisissons, pour chaque n  N*, un entier mn vérifiant
N*, un entier mn vérifiant
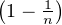 mn+1 ≤
mn+1 ≤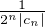 . Pour des raisons de simplicité de rédaction, on supposera sans perte de
généralité que la suite (mn) est croissante. Posons :
. Pour des raisons de simplicité de rédaction, on supposera sans perte de
généralité que la suite (mn) est croissante. Posons :
![{sin(πx) [c0- ∑+ ∞ n+1 (-1- ∑mn -xk-)]
f(x)= π x + n=1(- 1) cn n-x - k=0 nk+1 six ⁄∈ N
cn six = n ∈ N](/numeros/RMS130-3/RMS130-31186x.png)
Montrons que cette fonction est bien définie et continue. Soit N  N*.
N*.
Pour x  [-(N - 1),N - 1], et n ≥ N, on a
[-(N - 1),N - 1], et n ≥ N, on a
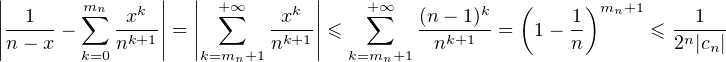
On en déduit que la série de fonctions
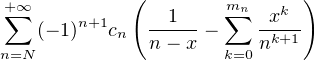
 [-(N - 1),N - 1], donc que f est bien définie et
continue sur ] - (N - 1),N - 1[\N. En outre, étant donné p
[-(N - 1),N - 1], donc que f est bien définie et
continue sur ] - (N - 1),N - 1[\N. En outre, étant donné p  ]] - (N - 1),N - 1[[, on peut pour
x
]] - (N - 1),N - 1[[, on peut pour
x  [-(N - 1), N - 1] \ N écrire f(x) comme somme de (-1)p+1cp
[-(N - 1), N - 1] \ N écrire f(x) comme somme de (-1)p+1cp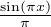
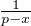 et d’une fonction
continue de x multipliée par sin(πx). Donc f(x)-→x→pcp. Ainsi, l’application f est bien définie
et continue.
et d’une fonction
continue de x multipliée par sin(πx). Donc f(x)-→x→pcp. Ainsi, l’application f est bien définie
et continue.
En outre, toujours pour x  [-(N - 1),N - 1], puisque
[-(N - 1),N - 1], puisque 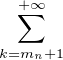 |cn|
|cn|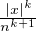 ≤
≤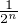 , la famille
, la famille
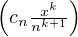 n≥N,k>mn est sommable et l’on a :
n≥N,k>mn est sommable et l’on a :
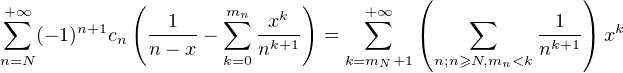
Par le théorème de Cauchy, l’application
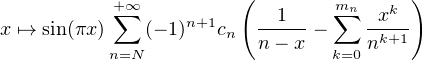
est développable en série entière sur [-(N - 1),N - 1].
Or, par le lemme, il en est de même de l’application
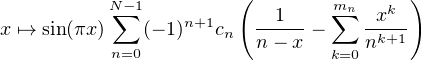
Donc f est développable en série entière sur [-(N - 1),N - 1]. Ceci étant vrai pour tout N  N*,
f est développable en série entière sur R (par unicité du développement en série entière, les
coefficients du développement en série entière sur [-(N - 1),N - 1] sont indépendants de
N).
N*,
f est développable en série entière sur R (par unicité du développement en série entière, les
coefficients du développement en série entière sur [-(N - 1),N - 1] sont indépendants de
N).
[RU] Walter Rudin, Analyse réelle et complexe, Dunod 3e édition.