 N, (an)n≥k+1 une suite réelle telle que
N, (an)n≥k+1 une suite réelle telle que 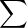 |an| converge et, pour x
|an| converge et, pour x  R,
f(x) =
R,
f(x) = 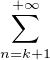 an cos(nx). Minorer le nombre de zéros de f sur [-π,π[.
an cos(nx). Minorer le nombre de zéros de f sur [-π,π[.
Solution de François Capacès
En prenant 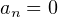 pour
pour 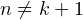 et
et 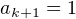 , on obtient
, on obtient 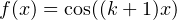 qui admet
exactement
qui admet
exactement 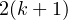 zéros sur
zéros sur 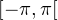 .
.
On va démontrer que si 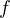 admet un nombre fini
admet un nombre fini 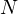 de zéros sur
de zéros sur 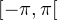 , alors
, alors 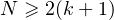 .
On a vu plus haut qu’il n’est pas possible de faire mieux. Nous utiliserons le fait que, pour
tout polynôme trigonométrique P de degré inférieur ou égal à k, on a
.
On a vu plus haut qu’il n’est pas possible de faire mieux. Nous utiliserons le fait que, pour
tout polynôme trigonométrique P de degré inférieur ou égal à k, on a 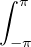 fP = 0,
résultat qui s’établit sans difficulté grâce à la convergence normale de la série définissant
f.
fP = 0,
résultat qui s’établit sans difficulté grâce à la convergence normale de la série définissant
f.
On considère les zéros de 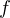 qui s’accompagnent d’un changement de signe ; ce qui est loisible
puisque les zéros de f sont en nombre fini et donc que le signe de la fonction est constant à gauche
et à droite du zéro. La fonction
qui s’accompagnent d’un changement de signe ; ce qui est loisible
puisque les zéros de f sont en nombre fini et donc que le signe de la fonction est constant à gauche
et à droite du zéro. La fonction 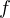 est paire, donc ces zéros sont non nuls et différents de
est paire, donc ces zéros sont non nuls et différents de 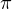 pour
des raisons de périodicité. Soit
pour
des raisons de périodicité. Soit  les zéros strictement positifs (avec changement de
signe). Les fonctions
les zéros strictement positifs (avec changement de
signe). Les fonctions
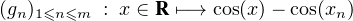
s’annulent en 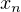 et
et 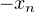 en changeant de signe et ne s’annulent pas ailleurs sur
en changeant de signe et ne s’annulent pas ailleurs sur 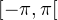 .
.
De ce fait la fonction 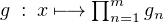 est un polynôme trigonométrique de degré inférieur ou
égal à
est un polynôme trigonométrique de degré inférieur ou
égal à 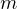 qui s’annule en changeant de signe en même temps que
qui s’annule en changeant de signe en même temps que 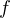 . En particulier
. En particulier 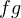 est de
signe constant sur
est de
signe constant sur 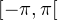 .
.
De plus 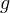 et
et 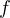 (pour des raisons de convergence normale) sont continues, donc
(pour des raisons de convergence normale) sont continues, donc 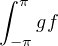 est non
nulle,
est non
nulle, 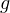 n’est pas orthogonale à
n’est pas orthogonale à 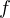 donc
donc 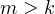 . Cela veut dire que le nombre de zéros
avec changement de signe de
. Cela veut dire que le nombre de zéros
avec changement de signe de 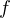 est
est 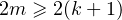 Donc on a, à plus forte raison,
Donc on a, à plus forte raison,
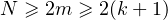 .
.
L’auteur de la solution nous signale que l’exercice est déjà paru dans le volume 105 de la revue,
année 94-95.
[Liste des corrigés]

