a) On suppose que (fn)n≥1 converge uniformément sur X vers une fonction f. Montrer que f est continue.
b) On suppose que X est compacte et que, pour toute suite (xn)n≥1 d’éléments de X et tout x de X tels que xn → x, on a fn(xn) → f(x). Montrer que f est continue et que la convergence est uniforme.
a) C’est du cours.
b) Notons tout d’abord que la suite (fn) converge simplement vers f (prendre des suites (xn)
constantes).
∙ (*) Notons aussi que toute suite extraite de (fn) a la même propriété. En effet si kp croît vers
+ ∞ et si (xp ) tend vers a 
X, la suite (yn) définie par yn = xp si n = kp et yn = a si n
n’est pas de la forme kp tend aussi vers a donc fn(yn) tend vers f(a) et en particulier
fkp (ykp ) = fkp (xp) tend vers f(a).
∙ Montrons maintenant que f est continue sur X. Soit a X et (xp) une suite de X tendant vers a.
La convergence simple de (fn) vers f permet de construire une suite strictement croissante d’entiers
(kp ) telle que ∀p, |fkp(xp) - f(xp)|≤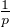
.
(*) s’applique à la suite (fkp) donc fkp(xp) tend vers f(a) et par suite f(xp) aussi.
∙ Pour vérifier que la convergence de (fn) vers f est uniforme considérons, pour tout n, xn X tel
que |fn (xn ) - f(xn)| = ∥fn - f∥∞. L’existence de xn est assurée par le théorème des
bornes.
Nous allons montrer que 0 est la seule valeur d’adhérence dans R de la suite de terme général mn = |fn (xn ) - f(xn)| ce qui permettra de conclure.
Pour cela considérons μ = limkmnk R une valeur d’adhérence. Comme X est compact quitte à
remplacer nk par une extraction on peut de plus supposer que xnk converge vers a X. D’après
(*) on voit alors que fnk(xnk) tend vers f(a) et donc que μ = 0.
En conclusion (mn) est une suite réelle qui n’a que 0 comme valeur d’adhérence dans R : elle
converge donc vers 0.
[Liste des corrigés]