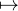 e-x
e-x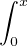 f(t)et d t.
f(t)et d t.
Voici deux solutions différentes de ce problème.
Solution par Jean-Claude Jacquens
On note g la fonction de R+ dans R : x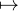 e-x
e-x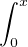 f(t)et d t.
f(t)et d t.
C’est la solution de l’équation différentielle yʹ + y = f(x) telle que y(0) = 0.
Pour tout x ≥ 0, on a 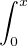 f2 =
f2 = 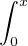 (gʹ + g)2 =
(gʹ + g)2 = 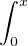 (g2 + 2ggʹ + gʹ2).
(g2 + 2ggʹ + gʹ2).
Notons F(x) = 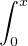 f2, G(x) =
f2, G(x) = 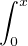 g2 et H(x) =
g2 et H(x) = 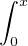 gʹ2.
gʹ2.
On a pour tout x ≥ 0, F(x) = g2(x) + G(x) + H(x).
Il s’ensuit que, pour tout x ≥ 0, G(x) ≤ F(x) ≤ f2 et H(x) ≤ F(x) ≤
f2 et H(x) ≤ F(x) ≤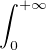 f2 car f2 est
intégrable sur R + . Comme g2 ≥ 0 et gʹ2 ≥ 0, les fonctions G et H sont croissantes ; elles ont une
limite finie en + ∞. Donc g2 est intégrable sur R+. Comme g2(x) = F(x) - G(x) - H(x), la
fonction g2 a une limite finie l en + ∞. L’intégrabilité de g2 implique l = 0. En conclusion g tend
vers 0 en + ∞.
f2 car f2 est
intégrable sur R + . Comme g2 ≥ 0 et gʹ2 ≥ 0, les fonctions G et H sont croissantes ; elles ont une
limite finie en + ∞. Donc g2 est intégrable sur R+. Comme g2(x) = F(x) - G(x) - H(x), la
fonction g2 a une limite finie l en + ∞. L’intégrabilité de g2 implique l = 0. En conclusion g tend
vers 0 en + ∞.
Solution par Enguerrand Moulinier
Il est souvent utile d’utiliser l’inégalité de Cauchy-Schwarz lorsque l’on manipule des fonctions
de carrés intégrables. Lorsqu’on l’applique brutalement ici, on peut montrer que cette
limite est majorée en valeur absolue par une constante. L’idée est de regarder ce qu’il
se passe sur ![[]
0,x2](/numeros/RMS130-3/RMS130-31081x.png) et
et ![[ ]
x2,x](/numeros/RMS130-3/RMS130-31082x.png) pour utiliser plusieurs majorations et gagner en finesse.
pour utiliser plusieurs majorations et gagner en finesse.
On notera M = limx→+∞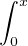 f(t)2 d t.
f(t)2 d t.
D’après l’inégalité de Cauchy-Schwarz, il vient :
 e-x e-x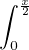 f(t) et d t f(t) et d t | ≤ e-x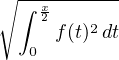 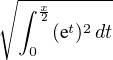 ≤ e-x ≤ e-x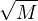 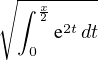 | ||
≤ e-x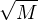 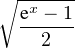 ≤ ≤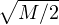 e- e-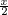 . . |
Il en résulte 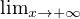 e-x
e-x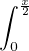 f(t) et d t = 0.
f(t) et d t = 0.
On fait le même calcul sur ![[x ]
2,x](/numeros/RMS130-3/RMS130-31097x.png) :
:
 e-x e-x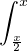 f(t) et d t f(t) et d t | ≤ e-x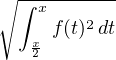 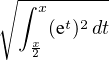 ≤ e-x ≤ e-x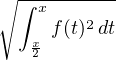 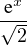 | ||
≤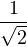 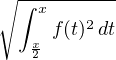 |
Or 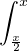 f(t)2 d t =
f(t)2 d t = 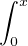 f(t)2 d t -
f(t)2 d t -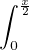 f(t)2 d t
f(t)2 d t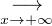 M - M = 0.
M - M = 0.
D’où e -x 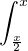 f(t) et d t
f(t) et d t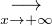 0.
0.
Finalement e -x 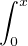 f(t) et d t = e-x
f(t) et d t = e-x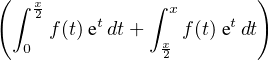
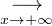 0.
0.
[Liste des corrigés]

