 RN définie par p0 = p1 = 1 et, pour n ≥ 2,
RN définie par p0 = p1 = 1 et, pour n ≥ 2,
pn = 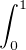
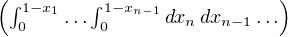 d x1. Calculer
d x1. Calculer 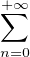 pn(π⁄6)n.
pn(π⁄6)n.
On définit par récurrence une suite (An)n N de fonctions polynomiales de [0,1] dans R en
posant
N de fonctions polynomiales de [0,1] dans R en
posant
A0 (x) = 1 et pour n ≥ 1, An(x) = 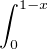 An-1(t)d t
An-1(t)d t
On constate que ∀n  N, pn = An(0).
N, pn = An(0).
On vérifie que An est à valeurs dans [0,1] et on définit à bon droit
F : [0, 1] → R , x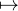
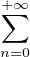 An(x)
An(x)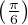 n.
n.
Pour n  N * , An ʹ(x) = -An-1(1 -x), donc |Anʹ(x)|≤ 1 si bien que F est de classe C1 et que,
pour x
N * , An ʹ(x) = -An-1(1 -x), donc |Anʹ(x)|≤ 1 si bien que F est de classe C1 et que,
pour x  [0, 1], Fʹ(x) = -
[0, 1], Fʹ(x) = -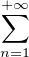 An-1(1 - x)
An-1(1 - x)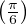 n = -
n = -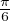 F(1 - x).
F(1 - x).
Donc F est de classe C2 et l’on a ∀x  [0,1], Fʹʹ(x) = -
[0,1], Fʹʹ(x) = -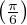 2F(x). On dispose donc de a,b
2F(x). On dispose donc de a,b  R
tels que
R
tels que
![πx- πx-
∀x ∈ [0,1],F (x) = acos 6 + bsin 6 (*)](/numeros/RMS130-3/RMS130-31061x.png)
Comme An (1) = δ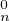 , on a F(1) = 1 d’où l’on déduit Fʹ(0) = -
, on a F(1) = 1 d’où l’on déduit Fʹ(0) = -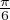 . En exploitant (*), on en déduit
que b = -1, a =
. En exploitant (*), on en déduit
que b = -1, a = 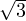 et donc
et donc
![(π π)
∀x ∈ [0,1],F(x) = 2cos 6x + 6](/numeros/RMS130-3/RMS130-31065x.png)
En particulier
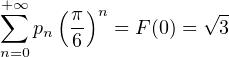
Remarque. La même méthode montre que, pour T  ] - 1,1[,
] - 1,1[,
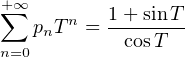
 C, |T| <
C, |T| < 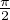 .
.

