∀x  R , (f(x), fʹ(x))≠(0,0).
R , (f(x), fʹ(x))≠(0,0).
a) Montrer que l’ensemble Z des zéros de f sur [0,2π[ est fini.
b) Soit g une fonction de classe C1 de R dans R tendant vers 1 en + ∞, vers - 1 en -∞.
Montrer que |Z| = -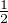
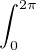 gʹ
gʹ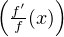
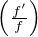 ʹ(x)d x.
ʹ(x)d x.
c) Montrer que |Z| = -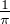
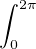
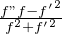 .
.
Solution de François Capacès
a) Soit x0  R un zéro de f. Comme fʹ(x0) ⁄= 0, on a f(x)~x→x0fʹ(x0)(x-x0) d’où f(x) ⁄= 0
au voisinage de x0. Les zéros de f sont donc isolés et, par conséquent, un segment n’en contient
qu’un nombre fini.
R un zéro de f. Comme fʹ(x0) ⁄= 0, on a f(x)~x→x0fʹ(x0)(x-x0) d’où f(x) ⁄= 0
au voisinage de x0. Les zéros de f sont donc isolés et, par conséquent, un segment n’en contient
qu’un nombre fini.
La fonction f admet donc un nombre fini de zéros sur [0,2π] donc aussi sur [0,2π[. On les notera

b) Posons aussi x0 = x1 - 2π et xn+1 = xn + 2π. La fonction f est de signe constant sur chacun
des intervalles ]xk,xk+1[, k  [[0,n]]. Si par exemple fʹ(xk) > 0, alors f > 0 sur ]xk,xk+1[ et
f < 0 sur ]xk-1 , xk[. On en déduit, quelque soit le signe de fʹ(xk) :
[[0,n]]. Si par exemple fʹ(xk) > 0, alors f > 0 sur ]xk,xk+1[ et
f < 0 sur ]xk-1 , xk[. On en déduit, quelque soit le signe de fʹ(xk) :
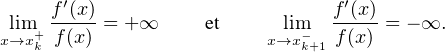
On a par ailleurs : 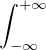 gʹ(u)d u = 2 d’où, en effectuant le changement de variable u =
gʹ(u)d u = 2 d’où, en effectuant le changement de variable u = 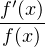 ,
x
,
x  ]xk , xk+1 [ :
]xk , xk+1 [ :
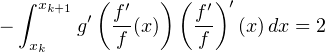
Finalement, en sommant sur k  [[1,n]] (ce qui est quelque peu abusif puisqu’il s’agit a priori
d’intégrales impropres) par 2π-périodicité :
[[1,n]] (ce qui est quelque peu abusif puisqu’il s’agit a priori
d’intégrales impropres) par 2π-périodicité :
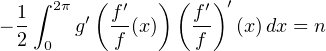
b) La fonction g : x  R
R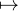
 arctan(x) est de classe
arctan(x) est de classe 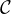 1 sur R et vérifie limx→±∞g = ±1. On
a
1 sur R et vérifie limx→±∞g = ±1. On
a
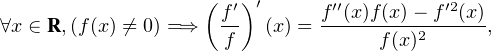
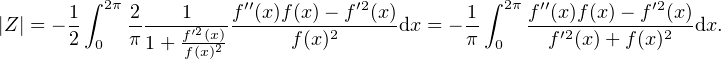
Puisque f et fʹ ne s’annulent pas en même temps, l’intégrale a priori n + 1 fois impropre du
départ s’avère pour ce choix de g être une pimpante intégrale tout ce qu’il y a de plus
propre.
[Liste des corrigés]

