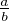 .
.
a) Pour n  N , montrer qu’il existe cn
N , montrer qu’il existe cn  Z tel que
Z tel que
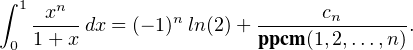
b) Soient n  N * et Pn =
N * et Pn = 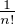
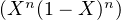 (n). Montrer qu’il existe A
n
(n). Montrer qu’il existe A
n  Z* tel
que
Z* tel
que
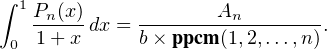
c) Soit, pour n  N, πn le nombre de nombres premiers inférieurs ou égaux à n. On admet
que πn ~
N, πn le nombre de nombres premiers inférieurs ou égaux à n. On admet
que πn ~ 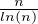 . Montrer que, pour n assez grand, ppcm(1,2,…,n) ≤ 3n.
. Montrer que, pour n assez grand, ppcm(1,2,…,n) ≤ 3n.
d) Conclure.
Solution de Lionel Ponton
Pour tout n  N , posons dn = ppcm(1,2,…,n) (avec la convention d0 = 1).
N , posons dn = ppcm(1,2,…,n) (avec la convention d0 = 1).
a) Soit n  N . Alors,
N . Alors,
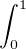 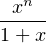 dx dx | = (-1)n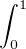 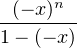 d x = (-1)n d x = (-1)n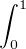 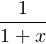 d x - (-1)n d x - (-1)n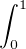 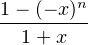 d x d x | ||
= (-1)n![[ln(1 + x)]](/numeros/RMS130-3/RMS130-31000x.png) 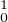 - (-1)n - (-1)n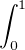 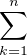 (-x)k-1 d x (-x)k-1 d x | |||
= (-1)n ln(2) + 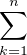 (-1)n+k (-1)n+k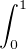 xk-1 d x = (-1)n ln(2) + xk-1 d x = (-1)n ln(2) + 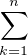 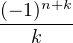 |
En écrivant le rationnel défini par la somme sous forme d’un quotient de deux entiers, on en déduit
qu’il existe cn  Z tel que
Z tel que
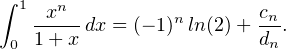
b) Commençons par remarquer que Pn est à coefficients entiers. En effet,
| Pn | =  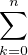 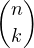 (Xn)(k)((1 - X)n)(n-k) (Xn)(k)((1 - X)n)(n-k) | ||
=  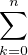 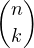 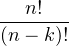 Xn-k Xn-k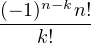 (1 - X)k (1 - X)k | |||
= 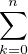 (-1)n-k (-1)n-k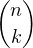 2Xn-k(1 - X)k 2Xn-k(1 - X)k |
qui est une somme de polynômes de Z[X] donc Pn  Z[X]. Par ailleurs, Pn est clairement de
degré n. crivons-le Pn =
Z[X]. Par ailleurs, Pn est clairement de
degré n. crivons-le Pn = 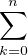 akXk avec ak
akXk avec ak  Z pour tout k
Z pour tout k  [[0,n]]. Alors, d’après la question a),
[[0,n]]. Alors, d’après la question a),
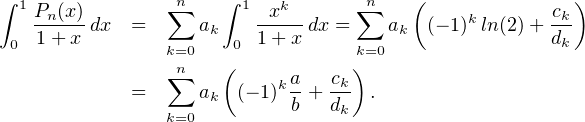
Comme ppcm (d0 ,d1,…,dn) = dn, on conclut qu’il existe An  Z tel que
Z tel que
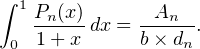
Reste à montrer An≠0. Pour cela, posons fn : x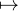
 xn(1 -x)n. Alors, par intégration par parties
successives,
xn(1 -x)n. Alors, par intégration par parties
successives,
![[ ]
∫1Pn(x) ∫ 1fn(n)(x) n-∑ 1 f(nn- k- 1)(x) 1 ∫ 1 fn(x)
1+xdx = -1-+-x dx = k!(1+-x)k+1- + n! (1-+x)n+1
0 0 k=0 0 0](/numeros/RMS130-3/RMS130-31024x.png)
Or, 0 et 1 sont racines d’ordre n de la fonction polynomiale fn donc
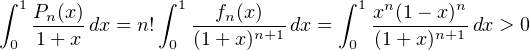
car la fonction intégrée est continue, positive et non identiquement nulle sur [0,1].
Ainsi, on conclut que An > 0 (et donc, comme An est entier, An ≥ 1).
c) Comme πn ~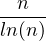 , pour tout réel k > 1, il existe nk
, pour tout réel k > 1, il existe nk  N tel que, pour tout n ≥ nk,
πn ≤ k
N tel que, pour tout n ≥ nk,
πn ≤ k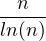 . Soit n ≥ 2, p un diviseur premier de dn et αp la valuation p-adique de dn. Alors, il
existe un entier j entre 1 et n tel que pαp divise j donc pαp ≤ n i.e. αp ln(p) ≤ ln(n). De plus, un
diviseur premier de dn est inférieur à n donc
. Soit n ≥ 2, p un diviseur premier de dn et αp la valuation p-adique de dn. Alors, il
existe un entier j entre 1 et n tel que pαp divise j donc pαp ≤ n i.e. αp ln(p) ≤ ln(n). De plus, un
diviseur premier de dn est inférieur à n donc
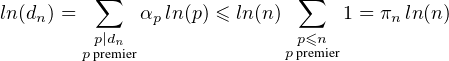
Dès lors, pour tout k > 1 et tout n ≥ nk, ln(dn) ≤ kn donc dn ≤ ekn. En prenant k = ln(3), on conclut que, pour n assez grand, dn ≤ 3n.
d) Les résultats de la question b) assurent que, pour tout n  N,
N,
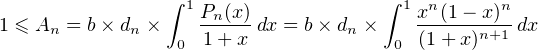
et donc, d’après la question c), il existe N  N tel que, pour tout entier n ≥ N,
N tel que, pour tout entier n ≥ N,
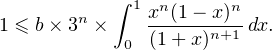
Or, pour tout réel x, x(1 - x) ≤ donc, pour tout n ≥ N,
donc, pour tout n ≥ N,
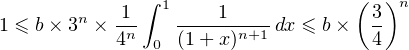
ce qui est absurde puisque le terme de droite tend vers 0 avec n.
Ainsi, ln (2) est irrationnel.

