112. Déterminer l’ensemble des nombres réels c tels qu’il existe une fonction deux fois dérivable f de R dans R telle que fʹ > f + c et fʹʹ > fʹ + c.

Solution de David Alexander

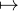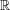Notons E l’ensemble des nombres réels c à déterminer. La fonction f : x↦→e2x est deux fois dérivable sur R et fʹʹ > fʹ > f, donc 0 ∈ E. Soient c ∈ E et f ∈ RR deux fois dérivable sur R telle que fʹ > f + c et fʹʹ > fʹ + c. Pour tout a ≤ c, on a fʹ > f + c ≥ f + a et fʹʹ > fʹ + c ≥ fʹ + a donc a ∈ E. Ce qui précède montre que E est un intervalle de R contenant ]- ∞, 0]. Soit c > 0. Supposons que c ∈ E. 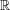Il existe alors f ∈ RR deux fois dérivable sur R telle que fʹ > f + c et fʹʹ > fʹ + c. Notons g: x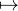↦→fʹ(x) - f(x) - cx. 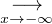Alors gʹ = fʹʹ- fʹ- c > 0 donc g est (strictement) croissante sur R et, de plus, ∀x ∈ R, g(x) > c-cx donc g(x) -→ x→ -∞ +∞, ce qui est contradictoire. Ceci montre que E ⊂]- ∞, 0]. Finalement, l’ensemble des nombres réels c cherchés est ]-∞,0].
[Liste des corrigés]


[ < ]