110. On considère n  N* et f1,…,fn des fonctions périodiques de R dans C telles que
g = f1 +
N* et f1,…,fn des fonctions périodiques de R dans C telles que
g = f1 +  + fn tende vers 0 en + ∞. Montrer que g = 0.
+ fn tende vers 0 en + ∞. Montrer que g = 0.
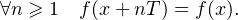
En
faisant tendre n → +∞, on obtient f(x) = 0, d’où f = 0.
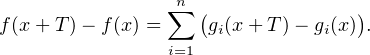
Or
x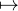 f(x + T) - f(x) converge encore vers 0 en + ∞, et les x
f(x + T) - f(x) converge encore vers 0 en + ∞, et les x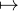 gi(x + T) - gi(x) sont encore
périodiques donc, par hypothèse de récurrence, x
gi(x + T) - gi(x) sont encore
périodiques donc, par hypothèse de récurrence, x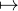 f(x + T) - f(x) est nulle. Donc f est
T-périodique et, tendant vers 0 en + ∞, est nulle.
f(x + T) - f(x) est nulle. Donc f est
T-périodique et, tendant vers 0 en + ∞, est nulle.
[Liste des corrigés]
 N* et f1,…,fn des fonctions périodiques de R dans C telles que
g = f1 +
N* et f1,…,fn des fonctions périodiques de R dans C telles que
g = f1 +  + fn tende vers 0 en + ∞. Montrer que g = 0.
+ fn tende vers 0 en + ∞. Montrer que g = 0.
Solution de Noé Weeks, élève au lycée Louis-le-Grand
Si n = 1, soit T une période (strictement positive) de f, et x 
 ; on a
; on a
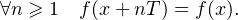
Pour passer au cas général, on est pris par l’envie de faire une récurrence. Satisfaisons-la. Soit
n ≥ 1 tel que le résultat soit vrai au rang n, et prenons g1,…,gn+1 périodiques telles que f = 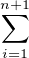 gi
tende vers 0 en + ∞. Soit T > 0 une période de gn+1 ; si x
gi
tende vers 0 en + ∞. Soit T > 0 une période de gn+1 ; si x 
 ,
,
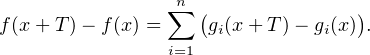
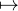 f(x + T) - f(x) converge encore vers 0 en + ∞, et les x
f(x + T) - f(x) converge encore vers 0 en + ∞, et les x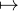 gi(x + T) - gi(x) sont encore
périodiques donc, par hypothèse de récurrence, x
gi(x + T) - gi(x) sont encore
périodiques donc, par hypothèse de récurrence, x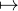 f(x + T) - f(x) est nulle. Donc f est
T-périodique et, tendant vers 0 en + ∞, est nulle.
f(x + T) - f(x) est nulle. Donc f est
T-périodique et, tendant vers 0 en + ∞, est nulle.
[Liste des corrigés]

