f(1) = 1 et ∀(x, y) (R⁺)²,f(x)f(y) ≤ f(xy).

L’ensemble E des fonctions répondant aux conditions du texte est non vide puisqu’il contient la fonction constante égale à 1 sur R₊.

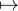Soit f E. Fixons x ⁺ et notons g_x: R₊ → R, yf(xy). On a :

∀y R ₊ , f(x)f(y) - f(1)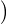 = f(x)f(y) - f(x) ≤ g_x(y) - g_x(1) (*)

Pour y > 1, en divisant les deux membres de (*) par y - 1 puis en passant à la limite quand y tend vers 1 par valeurs supérieures , on obtient : fʹ(1)f(x) ≤ xfʹ(x).

Pour y < 1, en divisant les deux membres de (*) par y - 1 puis en passant à la limite quand y tend vers 1 par valeurs inférieures, on obtient : fʹ(1)f(x) ≥ xfʹ(x).

Ainsi, pour tout x R₊, xfʹ(x) = fʹ(1)f(x). En posant a = fʹ(1), on déduit qu’il existe une constante λ telle que f(x) = λx^a sur . Comme f(1) = 1, λ = 1 et ∀x , f(x) = x^a. La fonction f étant dérivable en 0, il faut : a = 0 ou a ≥ 1.

Réciproquement, il est immédiat que toute fonction f : R₊ → R, x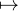x^a où a 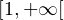∪ 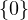appartient à E. Dans tous les cas, l’inégalité fonctionnelle vérifiée par f est en fait une égalité.

[Liste des corrigés]