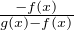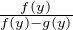105. Soient f et g deux fonctions convexes continues de [0,1] dans R telles que

∀x ∈ [0, 1], max (f(x),g(x)) ≥ 0.

Montrer qu’il existe λ ∈ [0,1] tel que ∀x ∈ [0,1],(1 - λ)f(x) + λg(x) ≥ 0.

∙ Soit A := {x ∈ [a,b]∣f(x) < 0} et B := {y ∈ [a,b]∣g(y) < 0}. Si A = ∅, on prend λ = 0 et si B = ∅, on prend λ = 1. On peut donc supposer A et B non vides ; on a évidemment A ∩ B = ∅.

∙ Soit λ ∈ [0, 1] ; on a

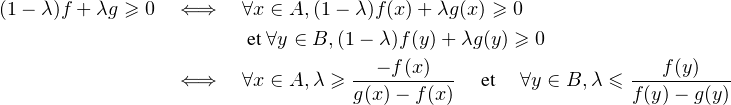
(1-λ)f+λg≥0 ⇐ ⇒ ∀x ∈ A,(1- λ)f(x)+ λg(x) ≥ 0 et∀y ∈ B,(1 - λ)f (y)+ λg(y) ≥ 0 - f(x) f(y) ⇐ ⇒ ∀x ∈ A,λ ≥ ---------- et ∀y ∈ B, λ ≤---------- g(x)- f(x) f(y)- g(y)
Il suffit donc d’établir que
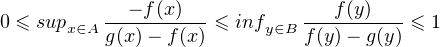
- f(x) f(y) 0 ≤ supx∈A g(x)--f(x) ≤ infy∈B f(y)--g(y) ≤ 1

Les comparaisons à 0 et 1 sont immédiates et il suffit donc d’établir le lemme suivant

Lemme 1.Pour x ∈ A et y ∈ B, --f(x)- g(x)-f(x) ≤--f(y)-- f(y)-g(y) (*)

Démonstration. Les deux segments [(x,g(x)),(y,g(y))] et [(x,f(x)),(y,f(y))] sont respectivement au dessus du graphe de g et de f. Formant les diagonales d’un trapèze, ils se coupent en un point M d’ordonnée Y . Comme M est au dessus du graphe de f et de g, on a Y ≥ 0.

Calculons Y . Pour un certain ρ ∈ [0,1], on a

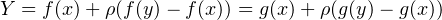
Y = f(x)+ ρ(f(y)- f(x)) = g(x )+ ρ(g(y)- g(x))

donc

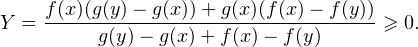
f (x)(g(y)- g(x))+ g(x)(f(x )- f(y)) Y = ------g(y)--g(x)+-f(x)--f(y)----- ≥ 0.

Puisque le dénominateur est strictement négatif, on a

f(x)(g(y) - g(x)) + g(x)(f(x) - f(y)) ≤ 0,

soit f(x)g(y) - g(x)f(y) ≤ 0 d’où l’on déduit (*).

Remarque : le résultat reste vrai en remplaçant [a,b] par une partie convexe non vide d’un espace vectoriel réel quelconque.
[Liste des corrigés]


[ < ]