
![]0,1[](/numeros/RMS130-3/RMS130-3874x.png) , soit Aλ l’ensemble des k de N* tels que le nombre de 9 dans l’écriture
décimale de k soit majoré par λnk, où nk est le nombre de chiffres de k. Étudier la
sommabilité de
, soit Aλ l’ensemble des k de N* tels que le nombre de 9 dans l’écriture
décimale de k soit majoré par λnk, où nk est le nombre de chiffres de k. Étudier la
sommabilité de 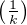 k
k Aλ.
Aλ.
Pour n  N * , notons An,λ l’ensemble des k
N * , notons An,λ l’ensemble des k  Aλ compris entre 10n-1 et 10n - 1 c’est-à-dire
l’ensemble des entiers à n chiffres et contenant au plus ⌊λn⌋ fois le chiffre 9. On a :
Aλ compris entre 10n-1 et 10n - 1 c’est-à-dire
l’ensemble des entiers à n chiffres et contenant au plus ⌊λn⌋ fois le chiffre 9. On a :
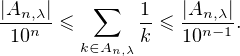
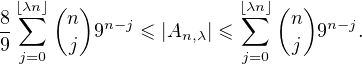
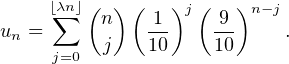
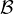 (n,1⁄10). On
a :
(n,1⁄10). On
a :
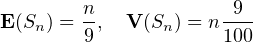
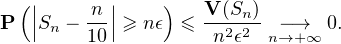
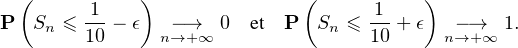
Si λ > 1⁄10, la série de terme général un diverge grossièrement donc la famille n’est pas sommable pour λ > 1⁄10.
Si λ < 1⁄10, il faut une utiliser une inégalité de concentration plus précise. Si t > 0,
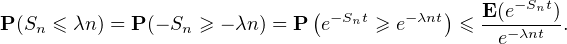
 + Xn) où les Xi sont i.i.d et suivent la loi de Bernoulli de paramètre 1⁄10
donc
+ Xn) où les Xi sont i.i.d et suivent la loi de Bernoulli de paramètre 1⁄10
donc
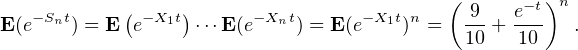
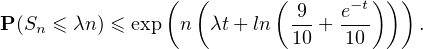
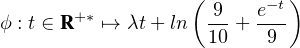
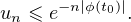
Enfin, pour λ = 1⁄10, le théorème limite central (très nettement hors programme !) donne la
convergence de (un) vers 1/2, donc la divergence grossière de la série de terme général un ; la
famille n’est pas sommable pour λ = 1⁄10.
[Liste des corrigés]

