 N*, soit N(d) le nombre de couples (m,n) de N*× N* tels que n ≤ m et
(m
n)
= d.
N*, soit N(d) le nombre de couples (m,n) de N*× N* tels que n ≤ m et
(m
n)
= d.
a) Montrer que (i,j)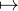 (i+j
j )
est strictement croissante en i et en j.
(i+j
j )
est strictement croissante en i et en j.
b) En considérant B = min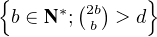 , montrer que N(d) = O(ln(d)).
, montrer que N(d) = O(ln(d)).
c) Montrer que 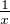
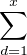 N(d)
N(d)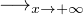 2.
2.
Nous corrigeons légèrement l’énoncé en restreignant l’étude aux couples 1 ≤ n < m, sans quoi
N(1) serait infini.
Remarquons tout d’abord que comme d = (d 1) = ( d d-1) , on a déjà N(d) ≥ 2 dès que d ≥ 3. Remarquons aussi que si d = (i+j j ) alors d = (i+j i ) de sorte que l’on a au moins la moitié des cas lorsque l’on rajoute la contrainte j ≤ i.
a) On a
(i+j+1
j)
⁄(i+j
j )
= 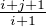 > 1 et (i+j+1
j+1 )
⁄(i+j
j )
=
> 1 et (i+j+1
j+1 )
⁄(i+j
j )
= 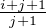 > 1.
> 1.
D’où le résultat demandé.
b) Considérons donc B comme indiqué dans l’énoncé, et x = (i+j j ) avec B ≤ j ≤ i. Alors par la question a) il vient
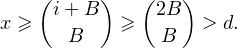
d > ( 2B-2 B-1 ) ≥ 2B-1,
de sorte que B ≤ 1 + log 2(d) et que N(d) ≤ 2 1 + log 2(d)
1 + log 2(d)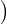 .
.
c) Le résultat que l’on cherche à obtenir est que, en dehors de ces cas triviaux, il est ≪ rare ≫ qu’un entier soit un coefficient binomial. On a
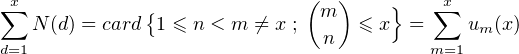
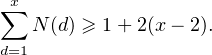
Il est facile de montrer qu’à m constant, les coefficients binomiaux (m
n)
sont strictement croissants
jusqu’au coefficient ≪ central ≫ ( m
⌊m⁄2⌋)
, puis strictement décroissants par symétrie. On en déduit
que
⊳ Si ( m 2 ) > x, alors um(x) = 2 (sous la contrainte que m ≤ x)
⊳ Si ( m 3 ) > x, alors um(x) ≤ 4.
La première condition est vérifiée lorsque m ≥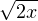 + 1, et la deuxième lorsque m ≥ (6x)1⁄3. On
en déduit que
+ 1, et la deuxième lorsque m ≥ (6x)1⁄3. On
en déduit que
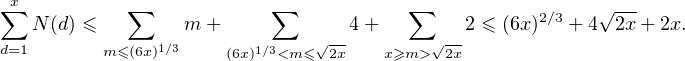
Cet encadrement est suffisant pour prouver que 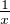
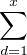 N(d)
N(d)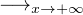 2.
2.
[Liste des corrigés]

